Cách khảo sát và vẽ đồ thị hàm số trên GeoGebra - Toán 12

a) Tính đạo hàm của hàm số trên một khoảng

Để tính đạo hàm của hàm số trên một khoảng, ta dùng lệnh Derivative(<hàm số>) hoặc DaoHam(<hàm số>), kết quả sẽ được hiển thị ngay bên dưới.

b) Tính đạo hàm của hàm số tại một điểm

Trước tiên, ta dùng lệnh Derivative(<hàm số>) hoặc DaoHam(<hàm số>), để tính đạo hàm của hàm số trên tập xác định của hàm số đó.

Nhấn nút ở đầu lệnh:

Lúc này, tên của hàm số được phần mềm đặt tự động.

Để tính đạo hàm của hàm số tại một điểm xác định, ta thay giá trị của biến vào hàm đạo hàm của hàm số đó, kết quả sẽ được hiển thị ngay bên dưới.

c) Để tính đạo hàm cấp n của hàm số trên một khoảng xác định, ta dùng lệnh Derivative(<hàm số>, <số cấp>) hoặc DaoHam(<hàm số>, <số cấp>), kết quả sẽ được hiển thị ngay bên dưới.

Để tìm cực trị của hàm số, ta dùng lệnh Extremum(<hàm số>) hoặc CucTri(<hàm số>), kết quả sẽ được hiển thị ngay bên dưới, dưới dạng toạ độ các điểm cực trị của hàm số.

Ngoài ra, ta có thể dùng lệnh Extremum(<hàm số>, <giá trị của a>, <giá trị của b>) hoặc CucTri(<hàm số>, <giá trị của a>, <giá trị của b>) để tìm cực trị của hàm số đã cho trên đoạn [a;b].

Kết quả trên (?, ?) có nghĩa: Hàm số đã cho không có cực trị nào trên khoảng (-5;0).

Chú ý: Ta có thể quan sát kênh hình để có hình ảnh trực quan bằng cách chọn View  Graphics 2.

Để xác định cực trị là cực đại hay cực tiểu, ta có thể dùng đồ thị hàm số để kết luận điểm cực trị là điểm cực đại hay điểm cực tiểu.

Để tìm giá trị lớn nhất của hàm số trên một đoạn [a;b] cho trước, ta dùng lệnh Max(<hàm số>, <a>, <b>) hoặc GTLN(<hàm số>, <a>, <b>); kết quả trả về sẽ là toạ độ của một điểm, tung độ của điểm đó chính là giá trị lớn nhất cần tìm.

Kết quả trên có nghĩa: Hàm số đã cho có giá trị lớn nhất trên đoạn [0;3] là 56, đạt tại x = 3.

Tương tự, để tìm giá trị nhỏ nhất của hàm số trên một đoạn [a;b] cho trước, ta dùng lệnh Min(<hàm số>, <a>, <b>) GTNN(<hàm số>, <a>, <b>); kết quả trả về sẽ là toạ độ của một điểm, tung độ của điểm đó chính là giá trị nhỏ nhất cần tìm.

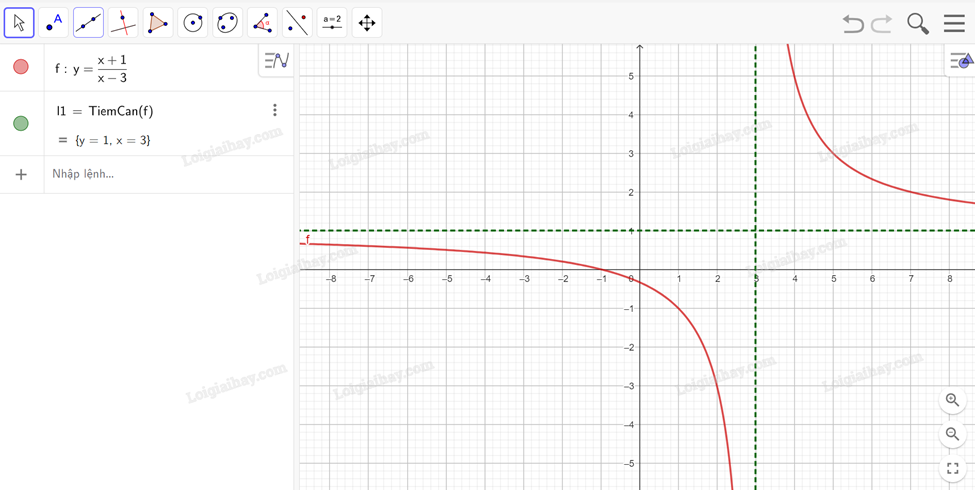
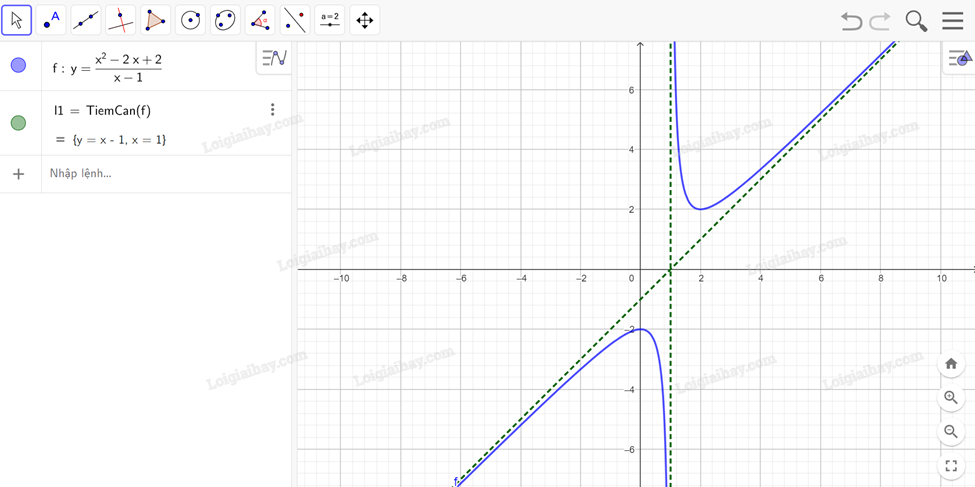
Để tìm các đường tiệm cận của đồ thị hàm số đã cho, ta dùng lệnh Asymptote(<hàm số>) hoặc TiemCan(<hàm số>); kết quả sẽ được hiển thị ngay bên dưới.

Kết quả trên có nghĩa: Đồ thị hàm số đã cho có hai đường tiệm cận là tiệm cận xiên y = x – 1 và tiệm cận đứng x = 3.

Kết quả trên có nghĩa: Đồ thị hàm số đã cho không có đường tiệm cận.

Khởi động GeoGebra và chọn View \( \to \) Graphics 2 để vẽ đồ thị hàm số. Khi đó, màn hình hiển thị sẵn hệ trục toạ độ dưới dạng lưới ô vuông.

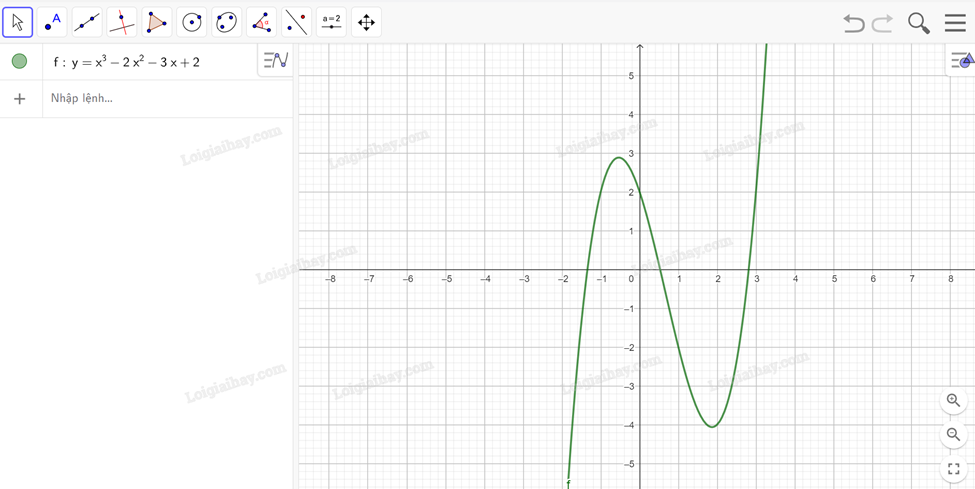
Bước 1: Vẽ đồ thị hàm số: Nhập hàm số vào ô lệnh.

Bước 2: Vẽ tiệm cận (nếu có): Dùng lệnh Asymptote(<hàm số>) hoặc TiemCan(<hàm số>).