1. Hướng dẫn chức năng của GeoGebra
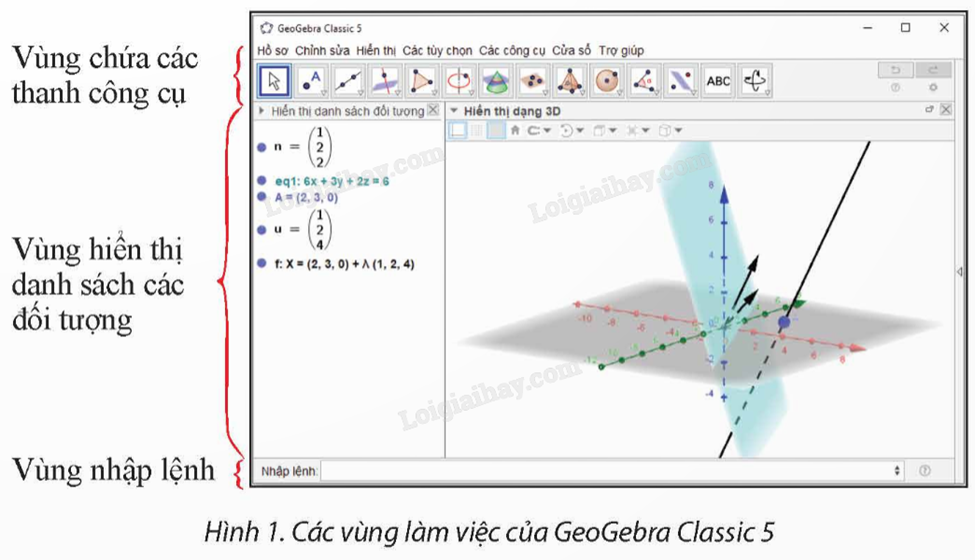
Để biểu diễn hình hoạ toạ độ trong không gian trên GeoGebra, ta thực hiện các thao tác trên bốn vùng sau:
1. Vùng chứa các thanh công cụ.
2. Vùng hiển thị danh sách các đối tượng.
3. Vùng hiển thị dạng 3D: chứa các điểm, vecto và mặt phẳng trong hệ trục toạ độ Oxyz.
4. Vùng nhập lệnh: để nhập toạ độ các điểm, vecto và mặt phẳng.
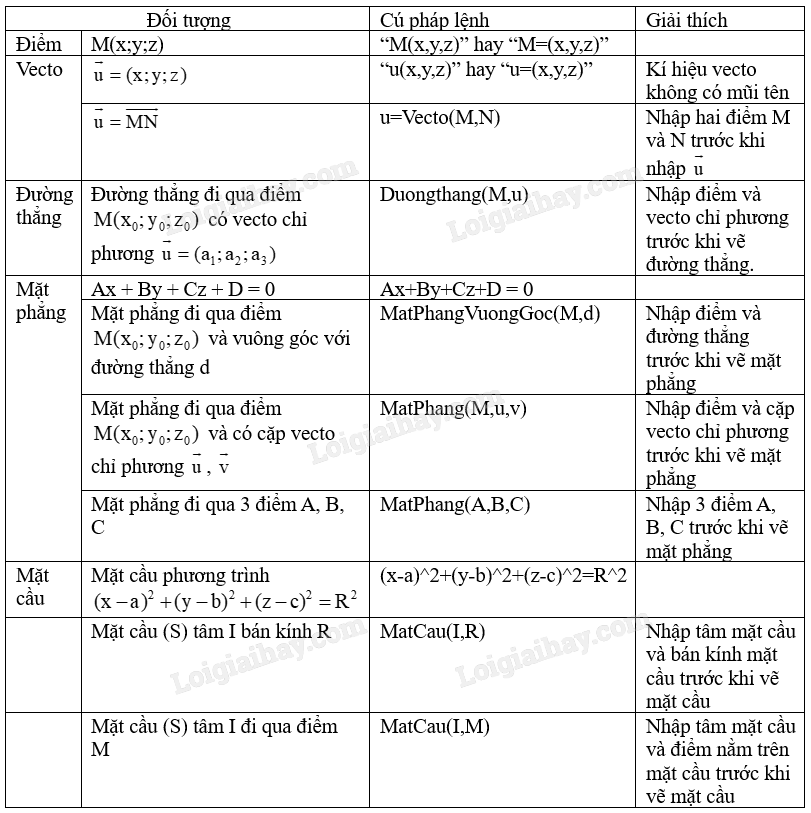
2. Cách biểu diễn các đối tượng hình học toạ độ trong không gian trên GeoGebra
3. Cách vẽ vecto tổng của ba vecto trong không gian bằng GeoGebra
Hoạt động:
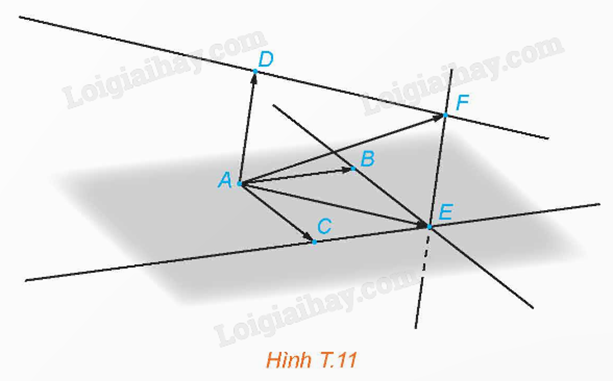
Lấy bốn điểm A, B, C, D trong không gian ba chiều và vẽ vecto \(\overrightarrow u = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
Hướng dẫn thực hiện:
Bước 1: Mở phần mềm GeoGebra, vào mục “Phối cảnh”/”Vẽ đồ hoạ 3D”.
Bấm chuột trái, chọn “Hiển thị hệ trục toạ độ” để tắt phần hiển thị hệ trục toạ độ.
Bước 2: Chọn công cụ “Điểm mới” để vẽ các điểm A, B, C, D trên mặt phẳng màu xám.
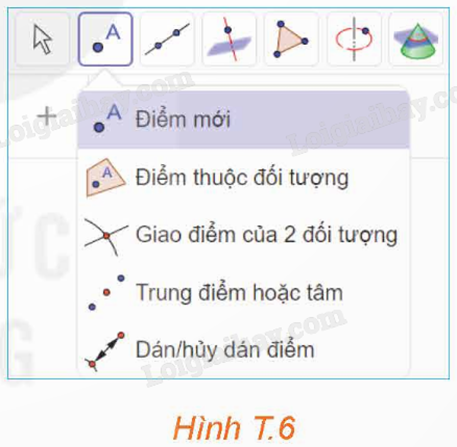
Chú ý: Ta có thể di chuyển các điểm bằng cách kích chuột phải vào điểm để hiện ra các mũi tên di chuyển 4 chiều và 2 chiều, sau đó di chuyển điểm theo hướng tương ứng với chiều mũi tên.

Bước 3: Sử dụng công cụ “Vecto qua 2 điểm” để vẽ ba vecto \(\overrightarrow {AB} \), \(\overrightarrow {AC} \), \(\overrightarrow {AD} \).
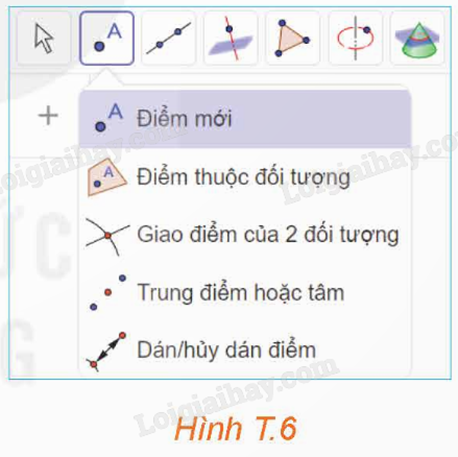
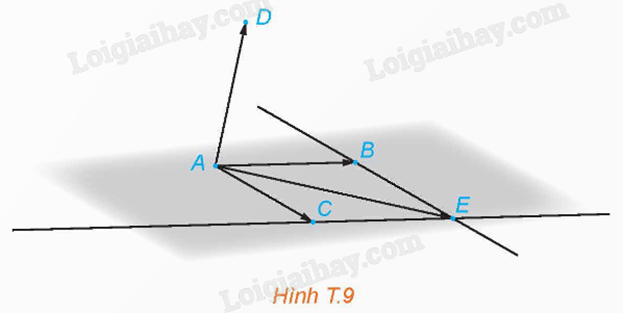
Bước 4: Sử dụng công cụ “Đường song song” để vẽ các đường thẳng song song với các vecto \(\overrightarrow {AB} \), \(\overrightarrow {AC} \).

Xác định giao điểm E của hai đường thẳng đó bằng công cụ “Giao điểm của 2 đối tượng”. Vẽ vecto \(\overrightarrow {AE} \).
Theo quy tắc hình bình hành, ta có \(\overrightarrow {AE} = \overrightarrow {AB} + \overrightarrow {AC} \).
Bước 5: Sử dụng công cụ “Đường thẳng song song” để vẽ các đường thẳng song song với các vecto \(\overrightarrow {AD} \), \(\overrightarrow {AE} \) và xác định giao điểm F của hai đường thẳng đó.
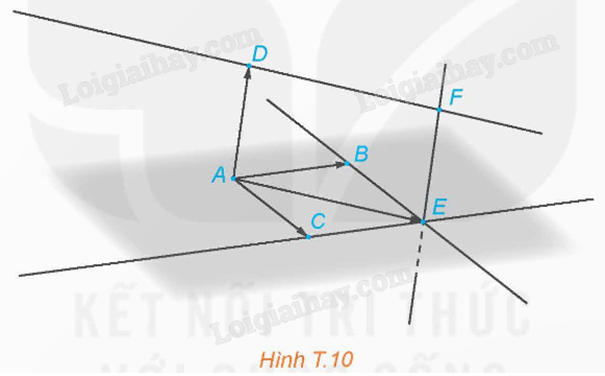
Bước 6: Vẽ vecto \(\overrightarrow {AF} \).
Theo quy tắc hình bình hành, ta có \(\overrightarrow {AF} = \overrightarrow {AE} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
Vậy \(\overrightarrow {AF} \) chính là vecto \(\overrightarrow u \) cần dựng.

 Thực hành sử dụng Geogebra - Từ điển Toán 12
Thực hành sử dụng Geogebra - Từ điển Toán 12 






Danh sách bình luận