Cách tính số trung bình, phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm trên Excel - Toán 12

Xét mẫu số liệu ghép nhóm cho bởi bảng sau:

* Phương sai:

- Công thức 1: \({S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\).

- Công thức 2: \({S^2} = \frac{1}{n}\left( {{n_1}{c_1}^2 + {n_2}{c_2}^2 + ... + {n_k}{c_k}^2} \right) - {\overline x ^2}\).

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu; \(\overline x  = \frac{1}{n}\left( {{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}} \right)\) là số trung bình.

* Độ lệch chuẩn: \(S = \sqrt {{S^2}} \).

Bảng tần số sau đây là dữ liệu thu được trên một nhóm học sinh khối lớp 12.

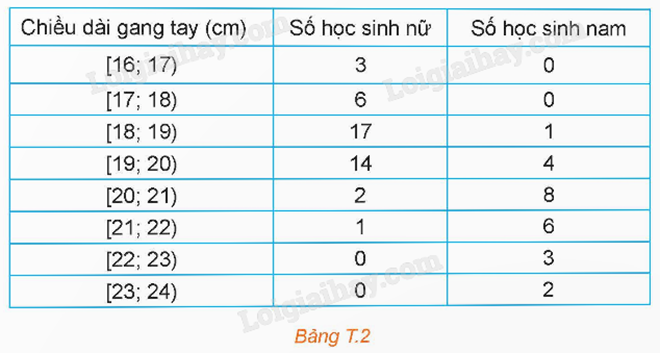
Bước 1: Nhập các đầu mút trái, đầu mút phải, tần số của các nhóm tương ứng vào các cột. Sau đó xác định điểm đại diện của từng nhóm.

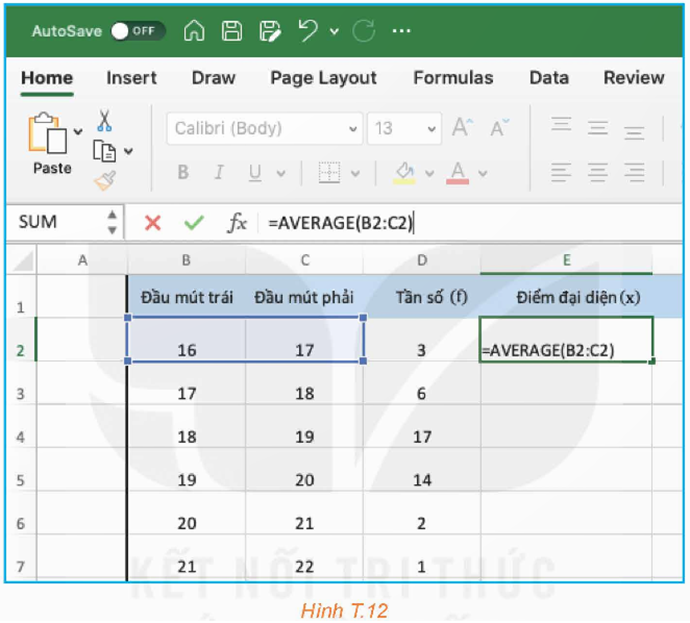
Bước 2: Nhân tần số với điểm đại diện của từng nhóm và tính tổng bằng cách dùng hàm SUM.

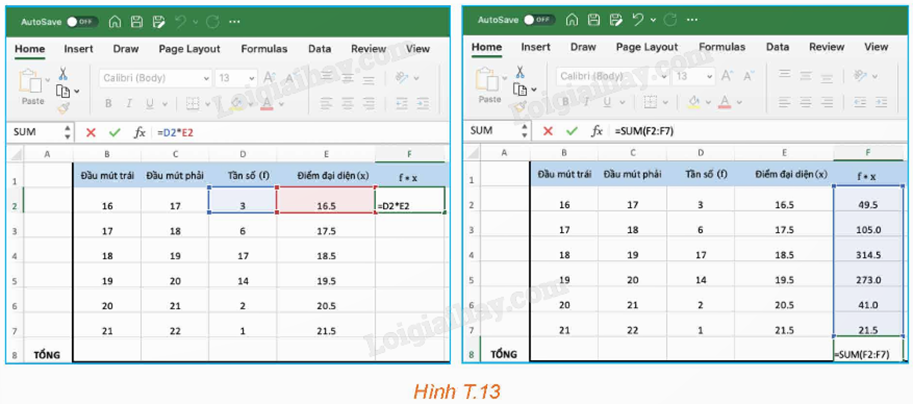
Bước 3: Tính tổng các tần số và thực hiện tính số trung bình. Kết quả thu được số trung bình bằng 18,71.

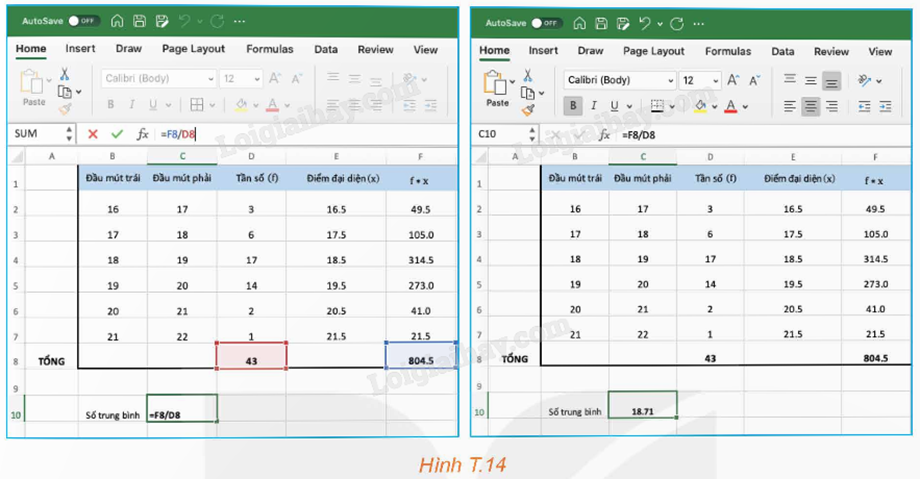
Bước 4: Để tính phương sai, độ lệch chuẩn, ta lần lượt lấy các điểm đại diện trừ đi số trung bình và bình phương kết quả.

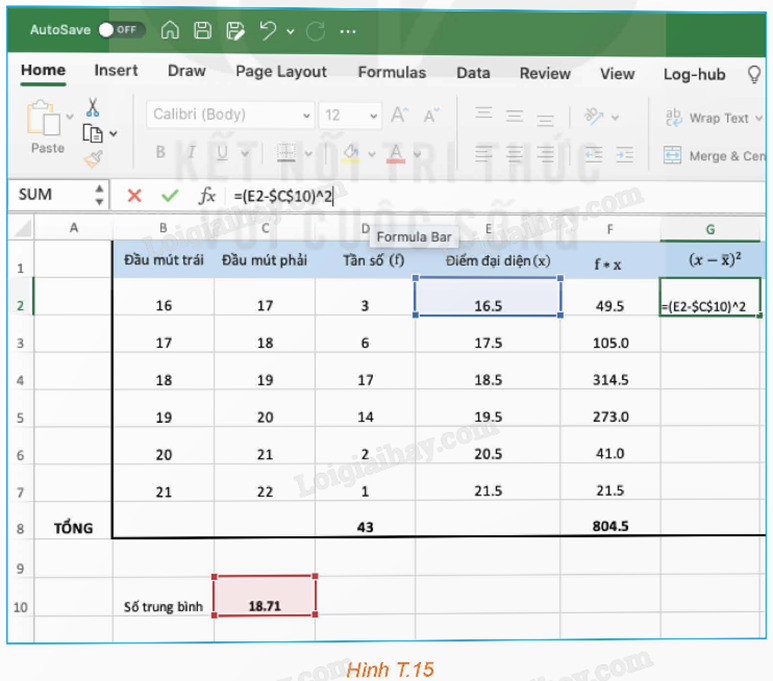
Bước 5: Lần lượt lấy tần số nhân với các bình phương vừa tạo ra ở Bước 4, rồi lấy tổng các kết quả thu được.

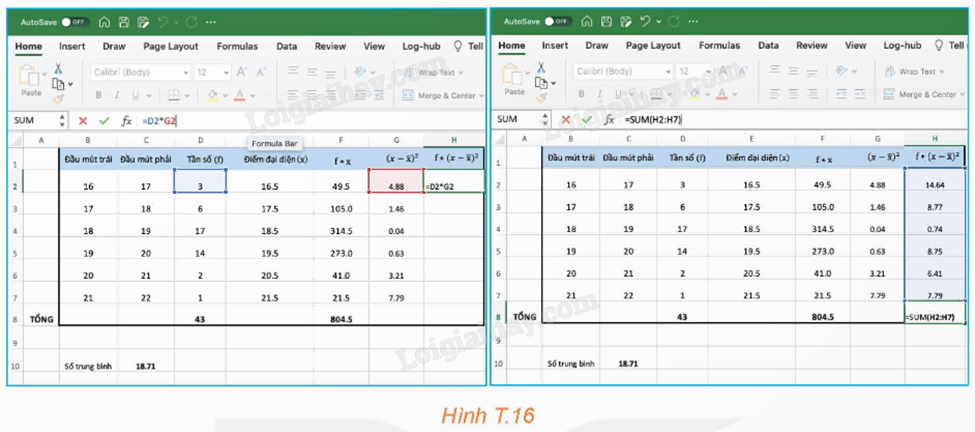
Bước 6: Tính phương sai, độ lệch chuẩn.

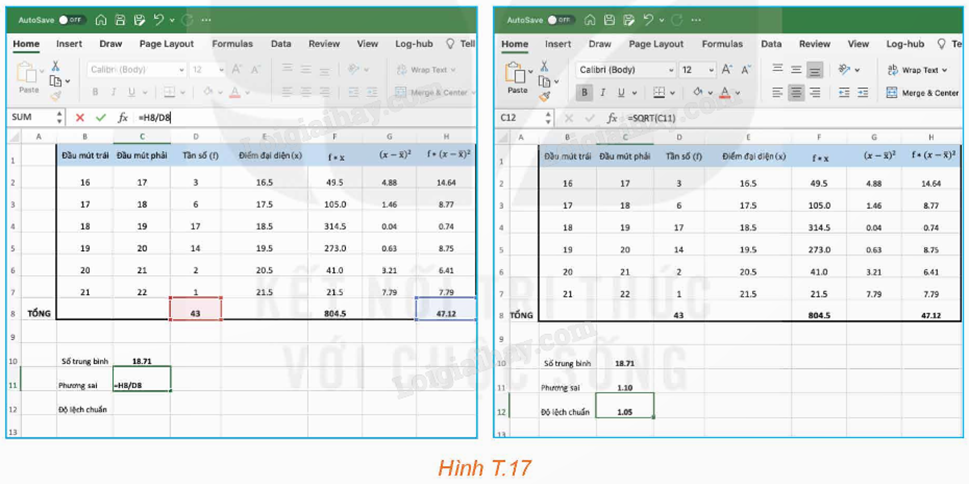
Kết quả thu được, phương sai của mẫu số liệu là 1,10 và độ lệch chuẩn là 1,05.