Cách sử dụng sơ đồ hình cây để tính xác suất có điều kiện - Toán 12

Cho hai biến cố A và B. Xác suất của biến cố A khi biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B và kí hiệu là P(A|B).

Cho hai biến cố A và B bất kì, với P(B) > 0. Khi đó:

\(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}\)

Trên sơ đồ hình cây:

+ Xác suất của các nhánh trong sơ đồ hình cây từ đỉnh thứ hai là xác suất có điều kiện.  

+ Xác suất xảy ra của mỗi kết quả bằng tích các xác suất trên các nhánh của cây đi đến kết quả đó.

1) Giả sử có 8 viên bi màu đỏ và 5 viên bi màu vàng trong một hộp. Từ 13 viên bi này, 5 viên bi được đánh số, trong đó có 3 viên bi màu đỏ. Ta cần tìm xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số.

Giải:

Xét hai biến cố sau:

A: “Viên bi được lấy ra có màu đỏ”.

B: “Viên bi được lấy ra có đánh số”.

Khi đó, xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số, chính là xác suất có điều kiện P(A∣B).

Sơ đồ hình cây biểu thị cách tính xác suất có điều kiện P(A∣B), được vẽ như sau:

Vậy xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó có đánh số là 0,6.

Ta có thể tính \[P\left( {A|B} \right) = \frac{{n(AB)}}{{N(B)}} = \frac{3}{5} = 0,6\].

2) Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T, xác suất để một ngày có gió là 0,6; nếu ngày có gió thì xác suất có mưa là 0,4; nếu ngày không có gió thì xác suất có mưa là 0,2. Gọi G là biến cố "Ngày có gió" và M là biến cố "Ngày có mưa".

a) Vẽ lại sơ đồ hình cây sau và điền vào ô ? các giá trị xác suất tương ứng:

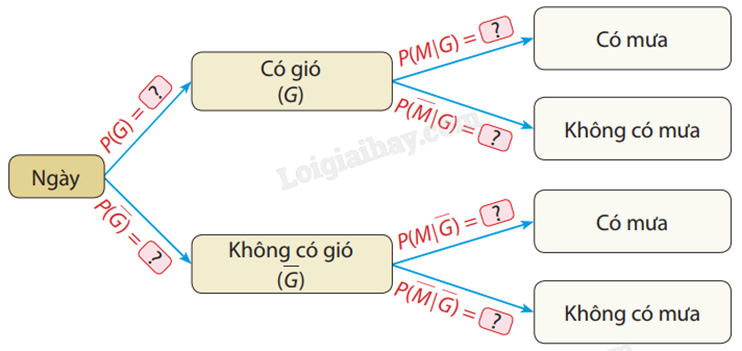
b) Tính xác suất P(GM) và \(P(G\overline M )\). Nêu ý nghĩa của các xác suất này.

Giải:

Theo đề bài, nếu ngày có gió thì xác suất có mưa là 0,4 nên \(P(M\mid G) = 0,4\).
Suy ra: \(P(\overline M \mid G) = 1 - 0,4 = 0,6\).

Ngày không có gió thì xác suất có mưa là 0,2 nên \(P(M\mid \overline G ) = 0,2\).

Suy ra: \(P(\overline M \mid \overline G ) = 1 - 0,2 = 0,8\).

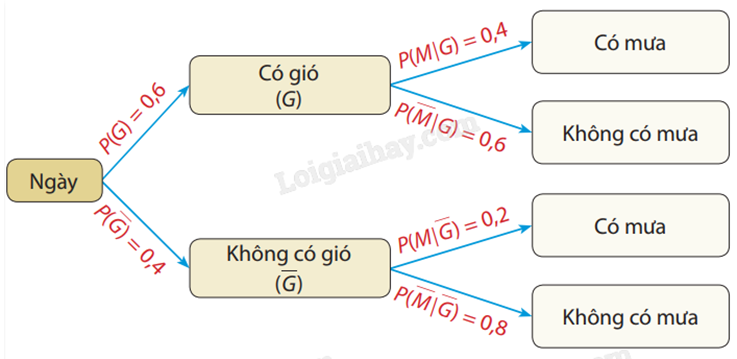
b) \(P(M\mid G) = P\left( G \right).P(M\mid G) = 0,6.0,4 = 0,24.\)

\(P(M\mid \overline G ) = P\left( G \right) \cdot P(M\mid G) = 0,6 \cdot 0,6 = 0,36.\)