1. Hàm số y = sinx
a) Khái niệm
Hàm số sin là quy tắc đặt tương ứng mỗi số thực x với số thực sinx, kí hiệu y = sinx.
b) Tính chất
- Tập xác định: \(D = \mathbb{R}\).
- Tập giá trị: [-1;1].
- Hàm số lẻ (đồ thị đối xứng qua gốc toạ độ O).
- Tuần hoàn với chu kì \(2\pi \).
- Đồng biến trên \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) \(\left( {k \in \mathbb{Z}} \right)\).
c) Đồ thị
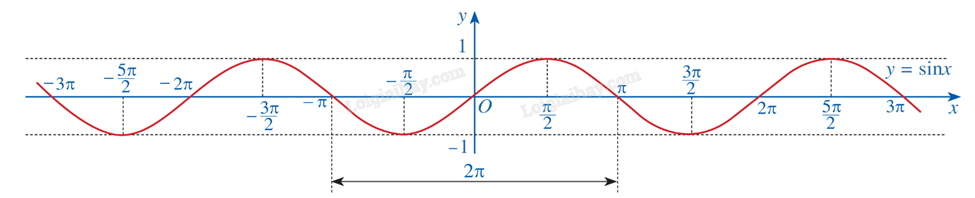
2. Hàm số y = cosx
a) Khái niệm
Hàm số cos là quy tắc đặt tương ứng mỗi số thực x với số thực cosx, kí hiệu y = cosx.
b) Tính chất
- Tập xác định: \(D = \mathbb{R}\).
- Tập giá trị: [-1;1].
- Hàm số chẵn (đồ thị đối xứng qua trục Oy).
- Tuần hoàn với chu kì \(2\pi \).
- Đồng biến trên \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên \(\left( {k2\pi ;\pi + k2\pi } \right)\) \(\left( {k \in \mathbb{Z}} \right)\).
c) Đồ thị
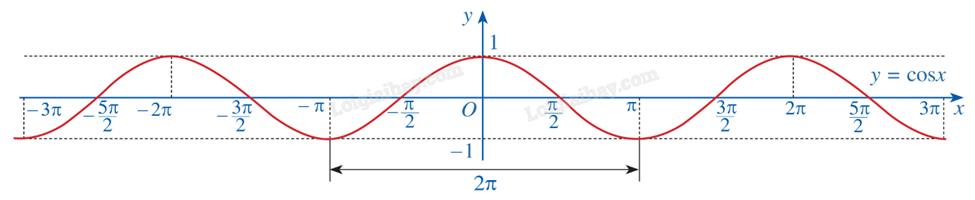
3. Hàm số y = tanx
a) Khái niệm
Hàm số tang là hàm số được xác định bởi công thức \(y = \frac{{\sin x}}{{\cos x}}\) với \(x \ne \frac{\pi }{2} + k\pi \), kí hiệu y = tanx.
b) Tính chất
- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
- Tập giá trị: \(\mathbb{R}\).
- Hàm số lẻ (đồ thị đối xứng qua gốc toạ độ O).
- Tuần hoàn với chu kì \(\pi \).
- Đồng biến trên \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) \(\left( {k \in \mathbb{Z}} \right)\).
c) Đồ thị
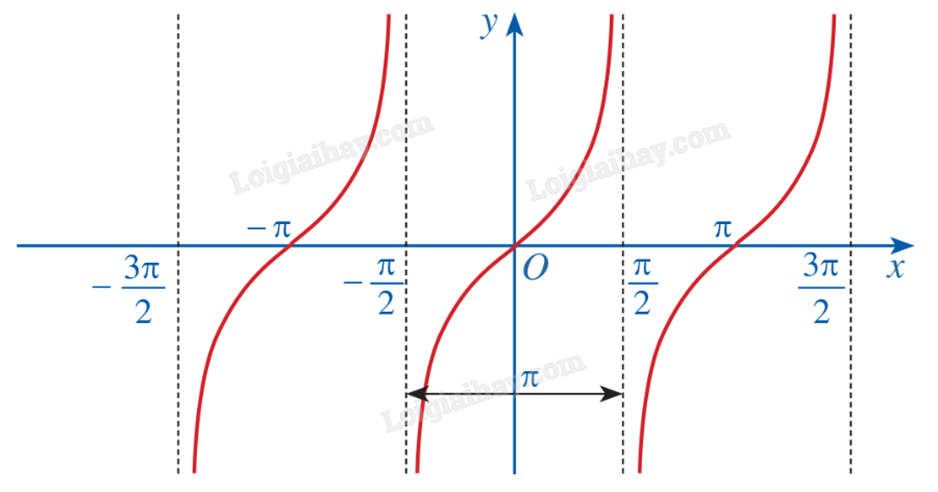
4. Hàm số y = cotx
a) Khái niệm
Hàm số cotang là hàm số được xác định bởi công thức \(y = \frac{{\cos x}}{{\sin x}}\) với \(x \ne k\pi \), kí hiệu y = cotx.
b) Tính chất
- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
- Tập giá trị: \(\mathbb{R}\).
- Hàm số lẻ (đồ thị đối xứng qua gốc toạ độ O).
- Tuần hoàn với chu kì \(\pi \).
- Nghịch biến trên \(\left( {k\pi ;\pi + k\pi } \right)\) \(\left( {k \in \mathbb{Z}} \right)\).
c) Đồ thị
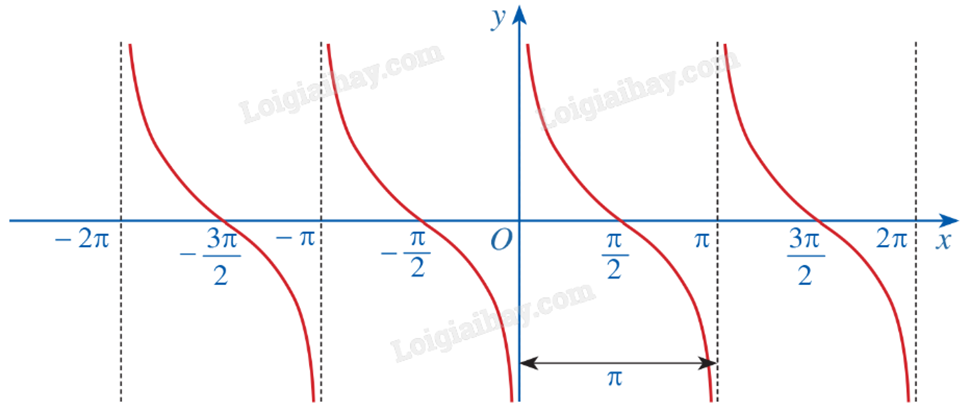

 Hàm số lượng giác - Từ điển môn Toán 11
Hàm số lượng giác - Từ điển môn Toán 11 






Danh sách bình luận