Lý thuyết Vecto trong không gian Toán 12 Cùng khám phá

1. Vecto trong không gian

1. Vecto trong không gian

Vecto trong không gian là một đoạn thẳng có hướng.

Ví dụ: Cho tứ diện ABCD. Hãy chỉ ra các vecto có điểm đầu A và điểm cuối là một trong các đỉnh còn lại của tứ diện.

Lời giải:

Ngoài đỉnh A, tứ diện còn có 3 đỉnh B, C, D nên ta có 3 vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \).

2. Độ dài của vecto. Hai vecto cùng phương, cùng hướng, bằng nhau

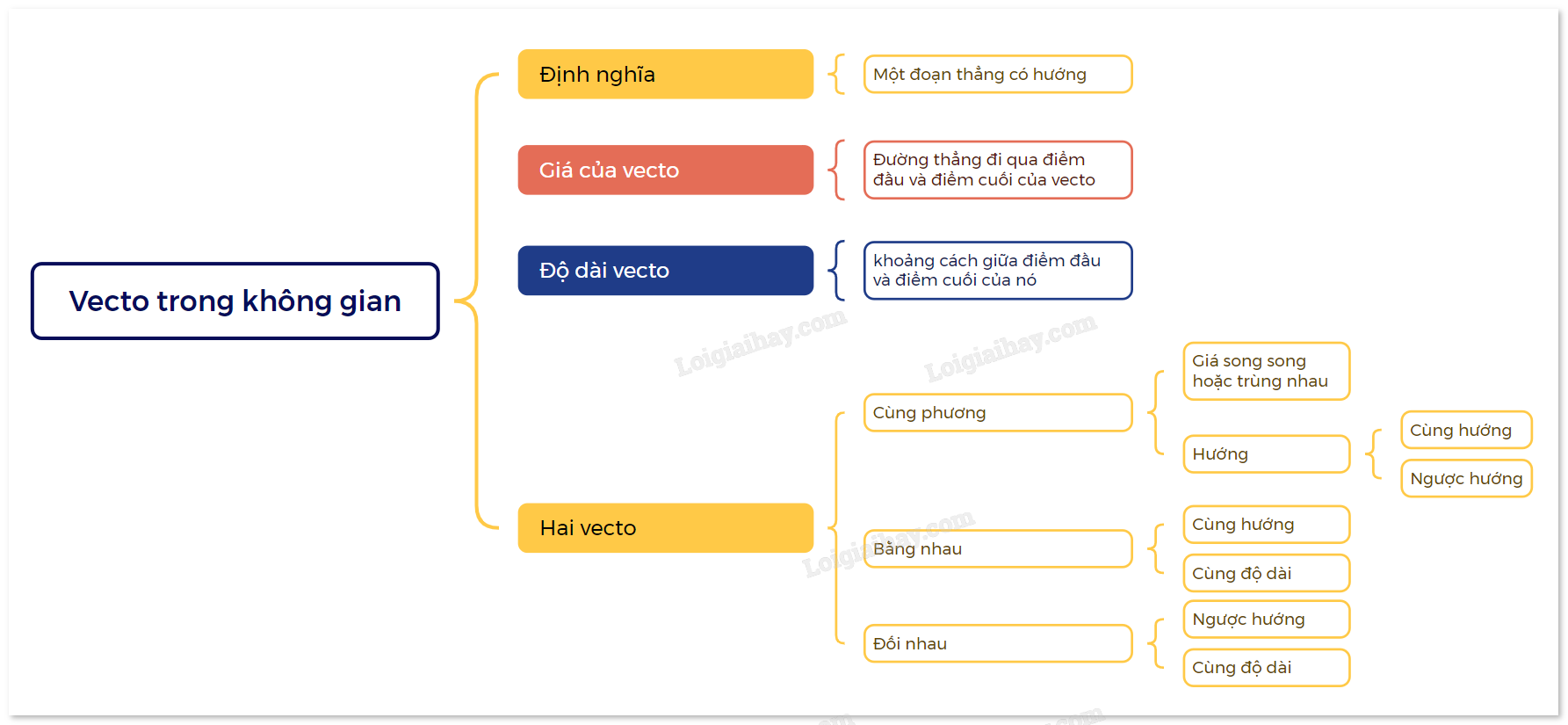
- Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vecto \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).

- Giá của vecto là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.

- Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

- Nếu hai vecto cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.

- Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

- Nếu hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng nhau thì ta viết \(\overrightarrow a = \overrightarrow b \)..

- Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng.

- Vecto đối của \(\overrightarrow a \) được kí hiệu là \( - \overrightarrow a \).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 51, 52 SGK Toán 12 tập 1 - Cùng khám phá
Trên công trường xây dựng, cần cẩu đang đưa một khung thép hình chữ nhật lên tầng cao của tòa nhà. Bốn dây cáp được móc vào bốn đỉnh của khung thép như ở Hình 2.1. Hãy biểu diễn trên hình vẽ hướng của các lực căng của bốn sợi dây cáp này.
Giải mục 2 trang 52, 53, 54 SGK Toán 12 tập 1 - Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng: - Độ dài của vectơ. - Giá của vectơ. - Hai vectơ cùng phương, hai vectơ cùng hướng. - Hai vectơ bằng nhau. - Hai vectơ đối nhau. - Vectơ-không.
Giải bài tập 2.1 trang 54 SGK Toán 12 tập 1 - Cùng khám phá
Cho hình tứ diện đều ABCD (Hình 2.5) a) Có bao nhiêu vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện? Liệt kê tất cả những vectơ đó. b) Bạn Lan nói: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)". Khẳng định của bạn Lan có đúng không? Vì sao?
Giải bài tập 2.2 trang 54 SGK Toán 12 tập 1 - Cùng khám phá
Cho hình chóp đều S.ABCD có cạnh đáy \(a\) và đường cao \(h\). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD và O, H lần lượt là tâm của các hình vuông ABCD, MNPQ (Hình 2.6). a) Trong những vectơ khác \(\vec O\), có điểm đầu và điểm cuối là những điểm cho trên hình, hãy liệt kê các vectơ: - Cùng hướng với \(\overrightarrow {MN} \); - Bằng \(\overrightarrow {MN} \). b) Tìm độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \) theo \(a\) và \(h\).