 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 1. Vecto trong không gian - Toán 12 Cùng khám phá
Bài 1. Vecto trong không gian - Toán 12 Cùng khám phá
Giải bài tập 2.1 trang 54 SGK Toán 12 tập 1 - Cùng khám phá
Cho hình tứ diện đều ABCD (Hình 2.5) a) Có bao nhiêu vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện? Liệt kê tất cả những vectơ đó. b) Bạn Lan nói: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)". Khẳng định của bạn Lan có đúng không? Vì sao?
Đề bài
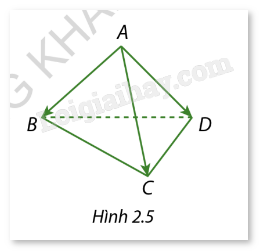
Cho hình tứ diện đều ABCD (Hình 2.5)
a) Có bao nhiêu vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện? Liệt kê tất cả những vectơ đó.
b) Bạn Lan nói: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)". Khẳng định của bạn Lan có đúng không? Vì sao?
Phương pháp giải - Xem chi tiết
- Sử dụng lý thuyết về vectơ để liệt kê các vectơ có điểm đầu và điểm cuối là các đỉnh của hình tứ diện.
- Sử dụng định nghĩa về vectơ bằng nhau để xác định tính đúng sai của khẳng định.
Lời giải chi tiết
a) Số lượng các vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện đều ABCD:
- Một tứ diện đều có 4 đỉnh: A, B, C, D.
- Số vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện đều là số cặp (không lặp lại) trong 4 đỉnh này.
Số lượng các vectơ là:
\(4 \times 3 = 12\)(vì mỗi đỉnh có 3 đỉnh còn lại để tạo vectơ)
Liệt kê các vectơ:
- Từ đỉnh \(A\): \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \)
- Từ đỉnh \(B\): \(\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {BD} \)
- Từ đỉnh \(C\): \(\overrightarrow {CA} ,\overrightarrow {CB} ,\overrightarrow {CD} \)
- Từ đỉnh \(D\): \(\overrightarrow {DA} ,\overrightarrow {DB} ,\overrightarrow {DC} \)
b) Khẳng định của bạn Lan: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)".
Để xét khẳng định này, ta cần kiểm tra:
- Độ dài của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) có bằng nhau không?
- Hướng của các vectơ này có cùng hướng không?
Trong hình tứ diện đều, các cạnh đều có độ dài bằng nhau:
\(|\overrightarrow {AB} | = |\overrightarrow {AC} | = |\overrightarrow {AD} |\)
Tuy nhiên, hướng của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) không cùng phương, vì:
- \(\overrightarrow {AB} \) là vectơ từ \(A\) đến \(B\)
- \(\overrightarrow {AC} \) là vectơ từ \(A\) đến \(C\)
- \(\overrightarrow {AD} \) là vectơ từ \(A\) đến \(D\)
Các vectơ này không song song với nhau mà tạo thành các góc với nhau trong không gian.
Vậy, khẳng định của bạn Lan là sai, vì các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) tuy có cùng độ dài nhưng không cùng phương và cùng hướng.
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận