 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 1. Vecto trong không gian - Toán 12 Cùng khám phá
Bài 1. Vecto trong không gian - Toán 12 Cùng khám phá
Giải mục 1 trang 51, 52 SGK Toán 12 tập 1 - Cùng khám phá
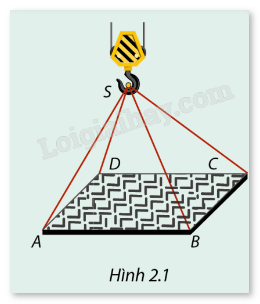
Trên công trường xây dựng, cần cẩu đang đưa một khung thép hình chữ nhật lên tầng cao của tòa nhà. Bốn dây cáp được móc vào bốn đỉnh của khung thép như ở Hình 2.1. Hãy biểu diễn trên hình vẽ hướng của các lực căng của bốn sợi dây cáp này.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 51 SGK Toán 12 Cùng khám phá
Trên công trường xây dựng, cần cẩu đang đưa một khung thép hình chữ nhật lên tầng cao của tòa nhà. Bốn dây cáp được móc vào bốn đỉnh của khung thép như ở Hình 2.1. Hãy biểu diễn trên hình vẽ hướng của các lực căng của bốn sợi dây cáp này.
Phương pháp giải:
- Xác định các lực căng trong các dây cáp.
- Sử dụng quy tắc hình bình hành để biểu diễn hướng của các lực căng.
- Phân tích lực tác động tại điểm treo S.
Lời giải chi tiết:
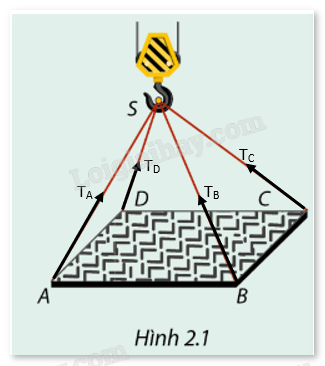
Các dây cáp SA, SB, SC, và SD đều chịu lực căng khi khung thép được nâng lên. Giả sử lực căng trong các dây lần lượt là \({T_A},{T_B},{T_C},{T_D}\).
Biểu diễn hướng của các lực căng:
- Lực căng \({T_A}\) trong dây cáp SA có phương từ điểm A đến điểm S.
- Lực căng \({T_B}\) trong dây cáp SB có phương từ điểm B đến điểm S.
- Lực căng \({T_C}\) trong dây cáp SC có phương từ điểm C đến điểm S.
- Lực căng \({T_D}\) trong dây cáp SD có phương từ điểm D đến điểm S.
Tại điểm S, tổng hợp các lực căng phải cân bằng với lực nâng của cần cẩu. Điều này có nghĩa là tổng hợp của \({T_A},{T_B},{T_C},{T_D}\) phải có phương thẳng đứng và cân bằng với trọng lượng của khung thép.
Trên hình vẽ, các lực căng được biểu diễn như sau:
- \({T_A}\) từ điểm A kéo về phía S.
- \({T_B}\) từ điểm B kéo về phía S.
- \({T_C}\) từ điểm C kéo về phía S.
- \({T_D}\) từ điểm D kéo về phía S.
LT1
Trả lời câu hỏi Luyện tập 1 trang 52 SGK Toán 12 Cùng khám phá
Cho hình chóp tứ giác S.ABCD. Hãy chỉ ra tất cả những vectơ có điểm đầu và điểm cuối là hai điểm phân biệt lấy trong các điểm S, A, B, C, D.
Phương pháp giải:
Liệt kê tất cả các điểm S, A, B, C, D.
Xác định tất cả các cặp điểm phân biệt có thể chọn từ 5 điểm này.
Từ mỗi cặp điểm, xác định 2 vectơ (một vectơ từ điểm đầu đến điểm cuối và một vectơ từ điểm cuối đến điểm đầu).
Lời giải chi tiết:
Đầu tiên, chúng ta liệt kê tất cả các điểm: S, A, B, C, D.
Bây giờ, chúng ta sẽ xác định tất cả các cặp điểm phân biệt:
1. \(S\) và \(A\): \(\overrightarrow {SA} \), \(\overrightarrow {AS} \)
2. \(S\) và \(B\): \(\overrightarrow {SB} \), \(\overrightarrow {BS} \)
3. \(S\) và \(C\): \(\overrightarrow {SC} \),\(\overrightarrow {CS} \)
4. \(S\) và \(D\): \(\overrightarrow {SD} \),\(\overrightarrow {DS} \)
5. \(A\) và \(B\): \(\overrightarrow {AB} \),\(\overrightarrow {BA} \)
6. \(A\) và \(C\): \(\overrightarrow {AC} \),\(\overrightarrow {CA} \)
7. \(A\) và \(D\): \(\overrightarrow {AD} \),\(\overrightarrow {DA} \)
8. \(B\) và \(C\): \(\overrightarrow {BC} \),\(\overrightarrow {CB} \)
9. \(B\) và \(D\): \(\overrightarrow {BD} \),\(\overrightarrow {DB} \)
10. \(C\) và \(D\): \(\overrightarrow {CD} \),\(\overrightarrow {DC} \)
Tóm lại, có tất cả 20 vectơ có điểm đầu và điểm cuối là hai điểm phân biệt lấy từ các điểm S, A, B, C, D.
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận