Lý thuyết Ứng dụng hình học của tích phân Toán 12 Cánh Diều

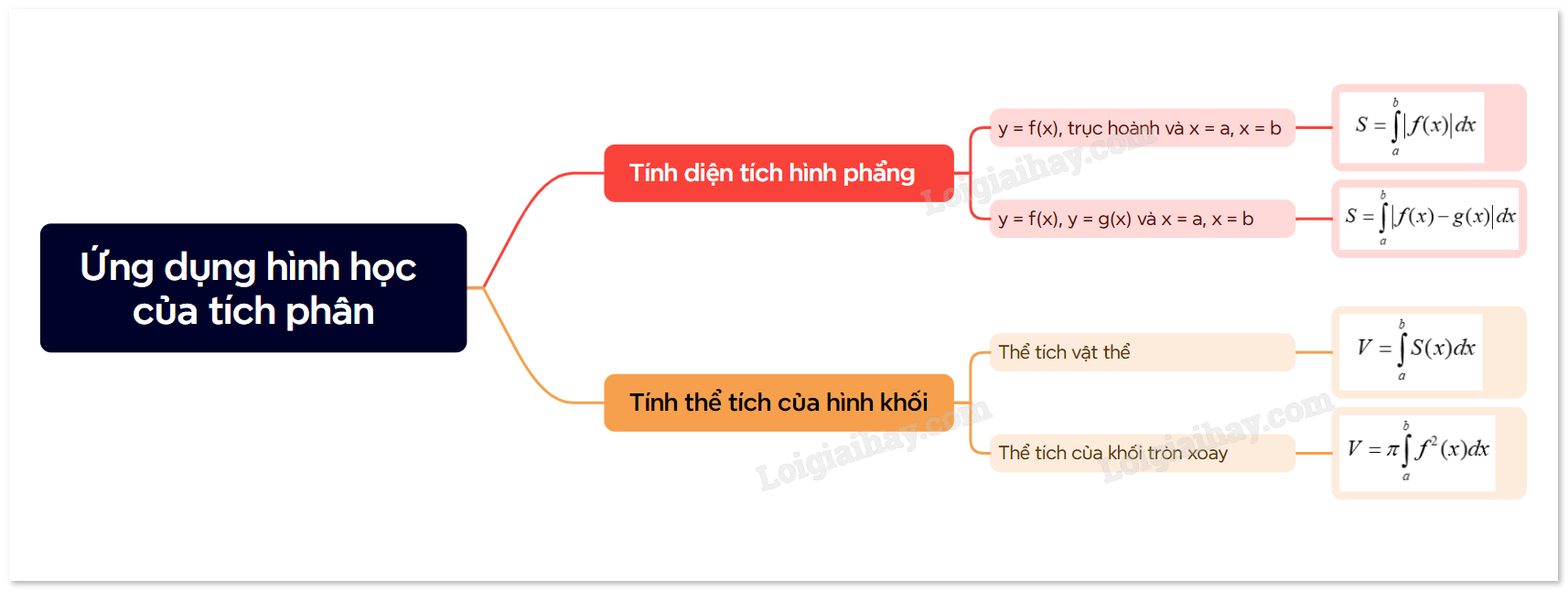
1. Tính diện tích hình phẳng a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức (S = intlimits_a^b {left| {f(x)} right|dx} )

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

1. Tính diện tích hình phẳng

a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b

Quảng cáo

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức

\(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)

b) Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b

Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = f(x), g(x) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng x = a, x = b được tính bằng công thức

\(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)

2. Tính thể tích của hình khối

Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\). Khi đó thể tích V của vật thể \(\beta \) được tính bởi công thức

\(V = \int\limits_a^b {S(x)dx} \)

b) Thể tích của khối tròn xoay

Cho hàm số f(x) liên tục, không âm trên đoạn \(\left[ {a;b} \right]\).

Khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay.

Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x).

Thể tích của khối tròn xoay này là:

\(V = \pi \int\limits_a^b {{f^2}(x)dx} \)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi mở đầu trang 28 SGK Toán 12 tập 2 - Cánh diều
Gốm Bát Tràng là tên gọi chung của các loại đồ gốm Việt Nam được sản xuất tại làng Bát Tràng, thuộc xã Bát Tràng, huyện Gia Lâm, Hà Nội. Với hơn 700 năm tuổi, gốm Bát Tràng nổi tiếng ở trong và ngoài nước về chất lượng gốm và độ tinh xảo của các sản phẩm. Những chiếc chén uống trà Hình 10 có dạng khối tròn xoay. Thể tích của các khối tròn xoay được tính như thế nào?
Giải mục 1 trang 28,29,30 SGK Toán 12 tập 2 - Cánh diều
Tính diện tích hình phẳng
Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều
Tính thể tích của hình khối
Giải bài tập 1 trang 39 SGK Toán 12 tập 2 - Cánh diều
Hình thang cong ABCD ở Hình 28 có diện tích bằng: A. (intlimits_1^2 {left( {frac{4}{x} - x + 3} right)dx} ) B. (intlimits_1^2 {left( {frac{4}{x} + x + 3} right)dx} ) C. (intlimits_1^2 {left( {frac{4}{x} - x - 3} right)dx} ) D. (intlimits_2^4 {left( {frac{4}{x} + x + 3} right)dx} )
Giải bài tập 2 trang 39 SGK Toán 12 tập 2 - Cánh diều
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số (f(x) = sqrt x ), trục hoành và hai đường thẳng x = 0, x = 2 quay quanh trục Ox là: A. (pi intlimits_0^2 {sqrt x dx} ) B. (pi intlimits_0^2 {xdx} ) C. (intlimits_0^2 {sqrt x dx} ) D. (intlimits_0^2 {xdx} )
Giải bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh diều
Cho đồ thị hàm số (y = {e^x}) và hình phẳng được tô màu như Hình 29 a) Hình phẳng đó được giới hạn bởi các đường nào? b) Tính diện tích hình phẳng đó
Giải bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều
Cho đồ thị các hàm số (y = {left( {frac{1}{2}} right)^x}), y = x + 1 và hình phẳng được tô màu như hình 30 a) Hình phẳng đó được giới hạn bởi các đường nào? b) Tính diện tích hình phẳng đó
Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều
Cho đồ thị hàm số (y = frac{1}{x}) và khối tròn xoay như Hình 31 a) Hình phẳng được giới hạn bởi các đường nào để khi xoay quanh trục Ox ta được khối tròn xoay như Hình 31? b) Tính thể tích khối tròn xoay đó
Giải bài tập 7 trang 41 SGK Toán 12 tập 2 - Cánh diều
Cho đồ thị hàm số y = f(t) như hình 32 a) Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f(t), trục Ot và hai đường thẳng t = 0, t = 2 b) Hỏi (intlimits_0^1 {f(u)du} ) biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32?
Giải bài tập 8 trang 41 SGK Toán 12 tập 2 - Cánh diều
Hình 34 minh họa mặt cắt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Đáy của con kênh là một đường cong cho bởi phương trình \(y = f(x) = \frac{3}{{100}}\left( { - \frac{1}{3}{x^3} + 5{x^2}} \right)\). Hãy tính diện tích hình phẳng tô màu xanh trong Hình 34, biết đơn vị trên mỗi trục tọa độ là mét
Giải bài tập 9 trang 41 SGK Toán 12 tập 2 - Cánh diều
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử \(\widehat {POM} = \alpha ,OM = l(0 \le \alpha \le \frac{\pi }{3};l > 0)\). Gọi \({\rm N}\) là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của \({\rm N}\) theo \(\alpha \) và \(l\)
Giải bài tập 10 trang 41 SGK Toán 12 tập 2 - Cánh diều
Sau khi đo kích thước của thùng rượu vang (Hình 36), bạn Quân xác định thùng rượu vang có dạng hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số (y = - 0,011{x^2} - 0,071x + 40), trục Ox và hai đường thẳng x = -35, x = 35 quay quanh trục Ox. Tính thể tích thùng rượu đó, biết đơn vị trên mỗi trục tọa độ là centimet
Giải bài tập 6 trang 40 SGK Toán 12 tập 2 - Cánh diều
Cho đồ thị hàm số y = f(t) như hình 32 a) Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f(t), trục Ot và hai đường thẳng t = 0, t = 2 b) Hỏi (intlimits_0^1 {f(u)du} ) biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32?