Giải chuyên đề học tập Toán lớp 11 Cánh diều
Bài 1. Phép dời hình Chuyên đề học tập Toán 11 Cánh diều
Giải mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 - Cánh diều
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Hoạt động 13
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Phương pháp giải:
- Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.
Kí hiệu: (Oa, Ob).
- Xác định điểm M' thỏa mãn điều kiện: OM' = OM và góc lượng giác (OM, OM') = 90°
Lời giải chi tiết:
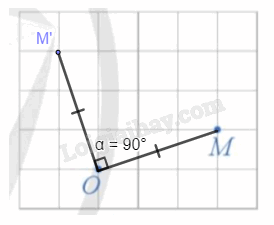
Cách xác định:
- Nối O với M;
- Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM.
Quảng cáo
Luyện tập 8
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác φφ không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho OM=OM′OM=OM′ và góc lượng giác (OM,OM′)=φ(OM,OM′)=φ được gọi là phép quay tâm O với góc quay φφ, kí hiệu Q(O,φ)Q(O,φ). O gọi là tâm quay, φφ gọi là góc quay.
Lời giải chi tiết:
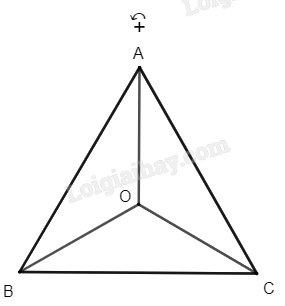
Ta có tam giác ABC đều có O là trọng tâm nên ^AOB=^BOC=^COA=120∘ˆAOB=ˆBOC=ˆCOA=120∘ và OA=OB=OCOA=OB=OC. Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B.
Hoạt động 14
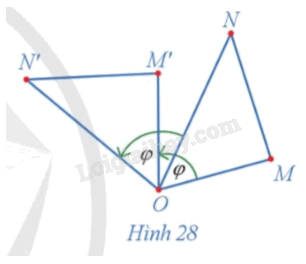
Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
Phương pháp giải:
Xét 2 tam giác OM'N' và OMN bằng nhau theo trường hợp c – g – c. Từ đó so sánh hai đoạn thẳng M'N' và MN.
Lời giải chi tiết:
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φφ nên OM=OM′,ON=ON′.OM=OM′,ON=ON′.
Ta có:
^MON+^NOM′=^MOM′=φ^NOM′+^M′ON′=^NON′=φ
Suy ra ^MON=^M′ON′
Xét hai tam giác OM'N' và OMN ta có:
OM = OM' (cmt)
^MON=^M′ON′ cmt)
ON = ON' (cmt)
Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c).
b) Từ ΔOM′N′=ΔOMN, suy ra M'N' = MN (hai cạnh tương ứng).
Hoạt động 15
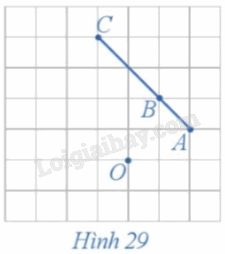
Xét phép quay tâm O với góc quay 90° (Hình 29).
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác φ không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho OM=OM′ và góc lượng giác (OM,OM′)=φ được gọi là phép quay tâm O với góc quay φ, kí hiệu Q(O,φ). O gọi là tâm quay, φ gọi là góc quay.
Lời giải chi tiết:
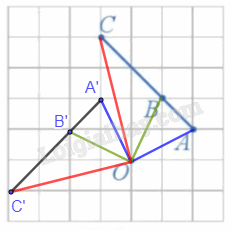
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên.
b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'.
Luyện tập 9
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
Phương pháp giải:
Tìm ảnh của tâm I qua phép quay bằng cách:
Phép quay tâm O, góc 900: Khi đó: {x′=−yy′=x
Từ đó xác định ảnh của (C)
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).
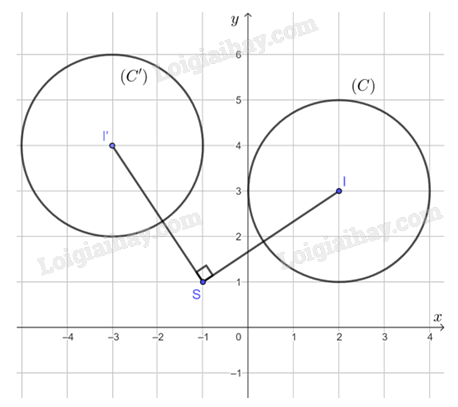
Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
Bình luận
Chia sẻ
- Giải mục 6 trang 21, 22 Chuyên đề học tập Toán 11 - Cánh diều
- Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 3 trang 23 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Giải bài 1 trang 72 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 3 trang 73 Chuyên đề học tập Toán 11 Cánh diều
- Giải khởi động trang 65 Chuyên đề học tập Toán 11 - Cánh diều
- Giải mục 1 trang 66, 67, 68, 69, 70 Chuyên đề học tập Toán 11 - Cánh diều
- Giải bài 1 trang 72 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 3 trang 73 Chuyên đề học tập Toán 11 Cánh diều
- Giải bài 2 trang 73 Chuyên đề học tập Toán 11 Cánh diều
- Giải mục 2 trang 71, 72 Chuyên đề học tập Toán 11 - Cánh diều
- Giải mục 1 trang 66, 67, 68, 69, 70 Chuyên đề học tập Toán 11 - Cánh diều
