Giải mục 2 trang 81 SGK Toán 8 – Cánh diều

Cho hai tam giác ABC và A’B’C’ có

Lựa chọn câu để xem lời giải nhanh hơn

HĐ2
LT3

HĐ2

Video hướng dẫn giải

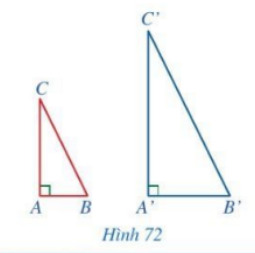
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (Hình 72). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\)

Phương pháp giải:

Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác đồng dạng.

Lời giải chi tiết:

Xét tam giác A’B’C’ và tam giác ABC có:

\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)

\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)

LT3

Video hướng dẫn giải

Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\). Chứng minh \(\widehat B = \widehat {B'}\).

Phương pháp giải:

- Từ tỉ lệ đã cho, suy ra tỉ lệ để chứng minh hai tam giác ABC và A’B’C’ đồng dạng theo trường hợp đồng dạng thứ hai.

- Suy ra hai góc bằng nhau theo định nghĩa tam giác đồng dạng.

Lời giải chi tiết:

Ta có: \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)

Hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ nên \(\widehat {A'} = \widehat A = 90^\circ \).

Xét tam giác ABC và tam giác A’B’C’ có:

\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat {A'} = \widehat A\)

\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c)

\( \Rightarrow \widehat B = \widehat {B'}\).