-
Toán 8 tập 1 - Cánh diều
-
Toán 8 tập 2 - Cánh diều
-
Chương 6 Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương 6
-
Chương 7 Phương trình bậc nhất một ẩn
-
Chương 8 Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài tập cuối chương 8
-
Giải bài 4 trang 82 SGK Toán 8 – Cánh diều
Cho Hình 77, chứng minh
Đề bài
Cho Hình 77, chứng minh
a) \(\widehat {ABC} = \widehat {BED}\)
b) \(BC \bot BE\)
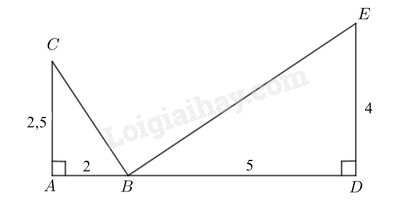
Hình 77
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta ABC \backsim \Delta DEB\) từ đó suy ra cặp góc bằng nhau.
b) Chứng minh \(\widehat {CBE} = 90^\circ \)
Lời giải chi tiết
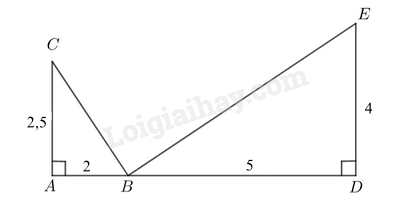
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).
Bình luận
Chia sẻ
- Giải bài 5 trang 82 SGK Toán 8 – Cánh diều
- Giải bài 6 trang 82 SGK Toán 8 – Cánh diều
- Giải bài 7 trang 82 SGK Toán 8 – Cánh diều
- Giải bài 3 trang 82 SGK Toán 8 – Cánh diều
- Giải bài 2 trang 82 SGK Toán 8 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
