Giải mục 2 trang 70, 71 SGK Toán 8 tập 1 - Kết nối tri thức

HĐ2

Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.

Phương pháp giải:

Dựa vào tính chất: hình vuông cũng là hình thoi và  hình chữ nhật

Lời giải chi tiết:

Hình vuông cũng là hình thoi, hình chữ nhật.

Mà hình chữ nhật có hai đường chéo bằng nhau còn hình thoi có hai đường chéo vuông góc với nhau.

Do đó, hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.

Câu hỏi

Hãy viết giả thiết, kết luận của câu a trong Định lí 4.

Phương pháp giải:

Vẽ hình và ghi giả thiết kết luận theo hình

Lời giải chi tiết:

Ta có thể viết giả thiết đối với cặp cạnh kề khác như: AB = BC; BC = CD; CD = AD.

Luyện tập 2

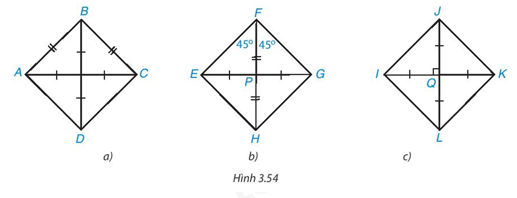
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?

Phương pháp giải:

Dựa vào các dấu hiệu nhận biết hình vuông

Lời giải chi tiết:

• Hình 3.54a)

Tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Suy ra tứ giác này là hình chữ nhật.

Mà AB = BC nên tứ giác ABCD là hình vuông.

Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

• Hình 3.54b)

Tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm P của mỗi đường.

Ta có \[\widehat {EFG} = \widehat {EFP} + \widehat {GFP} = {45^o} + {45^o} = {90^o}\]

Suy ra tứ giác EFGH là hình chữ nhật.

Hình chữ nhật EFGH có đường chéo FH là đường phân giác của \(\widehat {EFG}\).

Do đó tứ giác EFGH là hình vuông.

Ta dùng dấu hiệu nhận biết: Hình chữ nhật có một đường chéo là đường phân giác của một góc của hình vuông.

 • Hình 3.54c)

Tứ giác IJKL có hai đường chéo IK và JL bằng nhau và cắt nhau tại trung điểm Q của mỗi đường.

Suy ra tứ giác IJKL là hình chữ nhật.

Mà IK ⊥ JL nên tứ giác IJKL là hình vuông.

Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai đường chéo vuông góc là hình vuông

Vận dụng

Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?

Hãy giải thích tại sao.

- Trong trường hợp a, ta được hình thoi.

- Trong trường hợp b, ta được hình vuông

Phương pháp giải:

Quan sát hình 3.46 và giải thích

Lời giải chi tiết:

- Trong trường hợp a:

Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.

Khi đó, tứ giác ABCD là hình thoi.

- Trong trường hợp b:

Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

Khi đó, tứ giác đã cho là hình vuông.