Giải mục 2 trang 27, 28 SGK Toán 12 tập 1 - Kết nối tri thức

Khảo sát và vẽ đồ thị hàm số đa thức bậc 3

Đề bài

Trả lời câu hỏi Luyện tập 1 trang 28 SGK Toán 12 Kết nối tri thức

Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - 2{x^3} + 3{x^2} - 5x\).

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về sơ đồ khảo sát hàm số bậc ba để khảo sát và vẽ đồ thị hàm số:

Sơ đồ khảo sát hàm số bậc ba

1. Tìm tập xác định của hàm số.

2. Khảo sát sự biến thiên của hàm số:

+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.

+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.

+ Tìm cực trị của hàm số.

+ Tìm các giới hạn tại vô cực, giới hạn vô cực.

+ Lập bảng biến thiên của hàm số.

3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.

Lời giải chi tiết

1. Tập xác định: \(D = \mathbb{R}\)

2. Sự biến thiên:

Ta có: \(y' = - 6{x^2} + 6x - 5 = - 6{\left( {x - \frac{1}{2}} \right)^2} - \frac{7}{2} \le - \frac{7}{2}\) với mọi \(x \in \mathbb{R}\)

Hàm số nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).

Hàm số không có cực trị.

Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 3{x^2} - 5x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( { - 2 + \frac{3}{x} - \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)

\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 3{x^2} - 5x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^3}\left( { - 2 + \frac{3}{x} - \frac{3}{{{x^2}}}} \right)} \right] = - \infty \)

Bảng biến thiên:

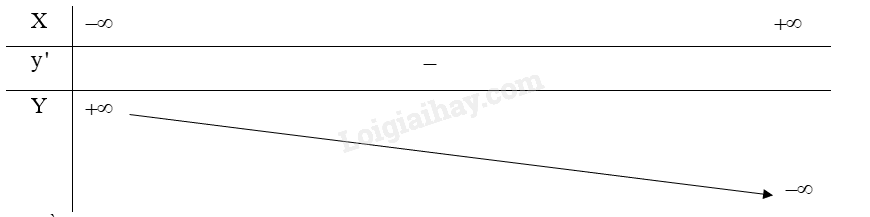
3. Đồ thị:

Giao điểm của đồ thị hàm số \(y = - 2{x^3} + 3{x^2} - 5x\) với trục tung là \(\left( {0;0} \right)\).

Ta có: \( - 2{x^3} + 3{x^2} - 5x = 0 \Leftrightarrow - x\left( {2{x^2} - 3x + 5} \right) = 0 \Leftrightarrow x = 0\). Do đó, giao điểm của đồ thị hàm số với trục hoành là điểm (0; 0).

Điểm \(\left( {1; - 4} \right)\) thuộc đồ thị hàm số \(y = - 2{x^3} + 3{x^2} - 5x\).

Đồ thị hàm số có tâm đối xứng là điểm \(\left( {\frac{1}{2}; - 2} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 - Kết nối tri thức
Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ
Giải bài tập 1.21 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) (y = - {x^3} + 3x + 1); b) (y = {x^3} + 3{x^2} - x - 1).
Giải bài tập 1.22 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) \(y = \frac{{2x + 1}}{{x + 1}}\); b) \(y = \frac{{x + 3}}{{1 - x}}\).
Giải bài tập 1.23 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) \(y = \frac{{2{x^2} - x + 4}}{{x - 1}}\); b) \(y = \frac{{{x^2} + 2x + 1}}{{x + 3}}\).
Giải bài tập 1.24 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức
Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc. a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x). b) Coi hàm C(x) là hàm số xác định với \(x \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này. c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.
Giải bài tập 1.25 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức
Trong Vật lí, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\) thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016). Giả sử một điện trở \(8\Omega \) được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là \(x\left( \Omega \right)\) thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số \(y = R\left( x \right),x > 0\) và dựa vào đ
Giải mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức
Sơ đồ khảo sát hàm số
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 Kết nối tri thức
1. Sơ đồ khảo sát hàm số