Bài 2. Tọa độ của một điểm và đồ thị của hàm số Toán 8 ..

Giải mục 2 trang 11, 12 SGK Toán 8 – Chân trời sáng tạo

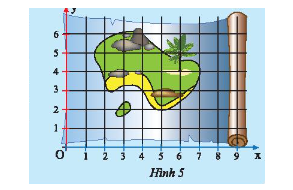
Bạn Khoa tìm được tấm bản đồ cổ cho biết kho báu của thuyền trưởng Độc Nhãn trên đảo Hòn Dừa (Hình 5) được dấu tại điểm có tọa độ (left( {6;4} right)). Em hãy kẻ một đường thẳng vuông góc với (Ox) tại điểm 6 và một đường thẳng vuông góc với (Oy) tại điểm 4. Xác định giao điểm của hai đường thẳng vừa vẽ để giúp bạn Khoa tìm kho báu.

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên

Lựa chọn câu để xem lời giải nhanh hơn

HĐ 2

Video hướng dẫn giải

Bạn Khoa tìm được tấm bản đồ cổ cho biết kho báu của thuyền trưởng Độc Nhãn trên đảo Hòn Dừa (Hình 5) được dấu tại điểm có tọa độ \(\left( {6;4} \right)\). Em hãy kẻ một đường thẳng vuông góc với \(Ox\) tại điểm 6 và một đường thẳng vuông góc với \(Oy\) tại điểm 4. Xác định giao điểm của hai đường thẳng vừa vẽ để giúp bạn Khoa tìm kho báu.

Phương pháp giải:

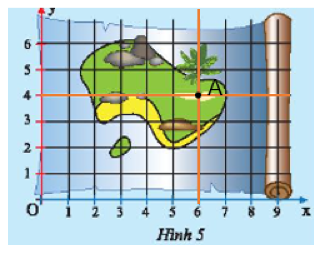
Kẻ đường thẳng vuông góc với \(Ox\) tại điểm 6 và một đường thẳng vuông góc với \(Oy\) tại điểm 4. Hai đường thẳng cắt nhau tại giao điểm cần tìm.

Lời giải chi tiết:

Đường thẳng vuông góc với \(Ox\) tại điểm 6 và đường thẳng vuông góc với \(Oy\) tại điểm 4 cắt nhau tại điểm \(A\) như hình vẽ.

TH 2

Video hướng dẫn giải

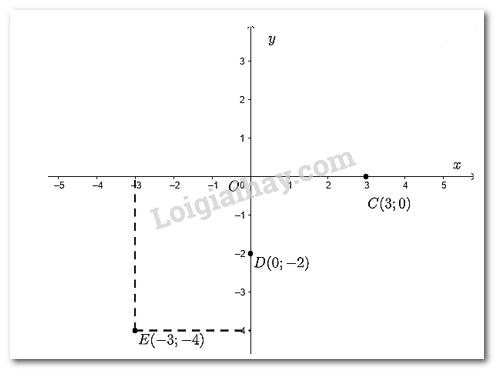
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(C\left( {3;0} \right);D\left( {0; - 2} \right);E\left( { - 3; - 4} \right)\)

Phương pháp giải:

Để xác định một điểm \(P\) có tọa độ là \(\left( {a;b} \right)\), ta thực hiện các bước sau:

- Tìm trên trục hoành điểm \(a\) và vẽ đường thẳng vuông góc với trục này tại điểm \(a\).

- Tìm trên trục tung điểm \(b\) và vẽ đường thẳng vuông góc với trục này tại điểm \(b\).

- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm \(P\)cần tìm.

Lời giải chi tiết:

- Đánh dấu điểm \(C\left( {3;0} \right)\)

Từ điểm 3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm 0 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\) (chính là trục \(Ox\)). Giao điểm của hai đường thẳng này chính là điểm \(C\left( {3;0} \right)\);

- Đánh dấu điểm \(D\left( {0; - 2} \right)\)

Từ điểm 0 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\)(chính là trục \(Oy\)); Từ điểm -2 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(D\left( {0; - 2} \right)\).

- Đánh dấu điểm \(E\left( { - 3; - 4} \right)\)

Từ điểm -3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm -4 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(E\left( { - 3; - 4} \right)\).

Ta có hình vẽ

VD 2

Người ta có thể dùng hai số để xác định vị trí của một điểm trên mặt đất hoặc địa cầu, chẳng hạn Lý Sơn là một huyện đảo nổi tiếng của Việt Nam, nằm ở vị trí \(109^0 07'3''\)Đ, \(15^0 22'51''\)B. Em hãy lấy một bản đồ địa lí Việt Nam và xác định vị trí của đảo Lý Sơn theo kinh độ và vĩ độ.

Phương pháp giải:

Để xác định một điểm \(P\) có tọa độ là \(\left( {a;b} \right)\), ta thực hiện các bước sau:

- Tìm trên trục hoành điểm \(a\) và vẽ đường thẳng vuông góc với trục này tại điểm \(a\).

- Tìm trên trục tung điểm \(b\) và vẽ đường thẳng vuông góc với trục này tại điểm \(b\).

- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm \(P\)cần tìm.

Lời giải chi tiết:

Học sinh tự thực hiện trên một bản đồ do thầy cô cung cấp.

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 6 phiếu

Bài tiếp theo

Giải mục 3 trang 12, 13 SGK Toán 8 – Chân trời sáng tạo
Làm thế nào để biểu diễn hàm số y=x trên mặt phẳng tọa độ?
Giải Bài 1 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Vẽ một hệ trục tọa độ (Oxy) và đánh dấu các điểm
Giải Bài 2 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Vẽ một hệ trục tọa độ (Oxy) và đánh dấu các điểm
Giải Bài 3 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Vẽ một hệ trục tọa độ (Oxy) và đánh dấu các điểm (Aleft( { - 3;3} right);Bleft( {3;3} right);Cleft( {3; - 3} right);Dleft( { - 3; - 3} right)). Nêu nhận xét về các cạnh và góc của tứ giác ABCD.
Giải Bài 4 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Vẽ đồ thị hàm số được cho bởi bảng sau:
Giải Bài 5 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Trong những điểm sau, tìm điểm thuộc đồ thị của hàm số
Giải Bài 6 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Cho (y) làm hàm số của biến số (x). Giá trị tương ứng của (x;y) được cho trong bảng sau:
Giải Bài 7 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Số quyển vở (x) đã mua và số tiền (y) (nghìn đồng) phải trả của ba bạn Hùng, Dũng, Mạnh được biểu diễn lần lượt bởi ba điểm (H,D,M) trong mặt phẳng tọa độ (Oxy) như Hình 11.
Giải Bài 8 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo
Mai trông coi một cửa hàng bán kem, em nhận thấy có mối quan hệ giữa số kem (S) bán ra mỗi ngày và nhiệt độ cao nhất (tleft( {^circ C} right)) của ngày hôm đó. Mai đã ghi lại các giá trị tương ứng của (t) và (S) trong bảng sau:
Giải mục 1 trang 10, 11 SGK Toán 8 – Chân trời sáng tạo
Trên biển có một con tàu ở vị trí A và một hòn đảo ở vị trí B (Hình 1). Hãy mô tả vị trí của con tàu và vị trí của hòn đảo so với vị trí của hai trục (Ox;Oy).
Giải Câu hỏi khởi động trang 10 SGK Toán 8 – Chân trời sáng tạo
Bạn Cúc mới học chơi cờ vua. Em hãy tìm giúp bạn:
Lý thuyết Tọa độ của một điểm và đồ thị của hàm số SGK Toán 8 - Chân trời sáng tạo
Tọa độ của một điểm là gì?