Giải mục 1 trang 83 SGK Toán 8 – Cánh diều

Cho hai tam giác ABC, A’B’C’ sao cho

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1
LT1

HĐ1

Video hướng dẫn giải

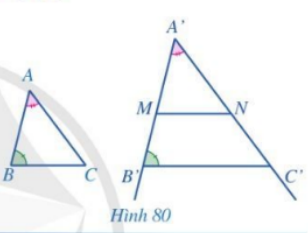
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) và \(A'B' \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A'M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A'MN = \Delta ABC\). Từ đó suy ra \(\Delta A'B'C' \backsim \Delta ABC\).

Phương pháp giải:

Chứng minh \(\Delta A'MN = \Delta ABC\) theo các trường hợp đã học từ đó chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).

Lời giải chi tiết:

Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)

\( \Rightarrow \widehat M = \widehat B\)

Xét tam giác A’MN và tam giác ABC có:

\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)

\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)

Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'B'C'\)

\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\)

LT1

Video hướng dẫn giải

Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).

Phương pháp giải:

Tìm số đo các góc còn lại của hai tam giác rồi chứng minh \(\Delta ABC \backsim \Delta MNP\) theo trường hợp đồng dạng thứ ba.

Lời giải chi tiết:

Xét tam giác ABC có:

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)

Xét tam giác ABC và tam giác MNP có:

\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)

\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).