 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 2. Các phép toán vecto trong không gian - Toán 12 C..
Bài 2. Các phép toán vecto trong không gian - Toán 12 C..
Giải mục 1 trang 55, 56, 57, 58 SGK Toán 12 tập 1 - Cùng khám phá
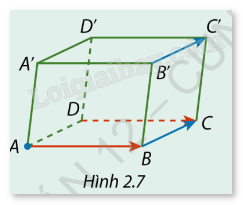
Cho hình hộp ABCD.A'B'C'D' (Hình 2.7). Một vật bắt đầu di chuyển từ điểm A theo độ dịch chuyển bằng \(\overrightarrow {DC} \), sau đó tiếp tục di chuyển theo độ dịch chuyển bằng \(\overrightarrow {B'C'} \). Hỏi vật sẽ di chuyển đến điểm nào?
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 55 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.A'B'C'D' (Hình 2.7). Một vật bắt đầu di chuyển từ điểm A theo độ dịch chuyển bằng \(\overrightarrow {DC} \), sau đó tiếp tục di chuyển theo độ dịch chuyển bằng \(\overrightarrow {B'C'} \). Hỏi vật sẽ di chuyển đến điểm nào?
Phương pháp giải:
1. Xác định điểm đến sau khi di chuyển theo vectơ đầu tiên.
2. Xác định điểm đến tiếp theo sau khi di chuyển theo vectơ thứ hai.
Lời giải chi tiết:
Bước 1: Di chuyển từ A theo độ dịch chuyển \(\overrightarrow {DC} \)
Điểm A dịch chuyển theo \(\overrightarrow {DC} \) tức là di chuyển theo đoạn DC nhưng bắt đầu từ A. Vì \(D\) và A nằm trên cùng một mặt phẳng, nên khi dịch chuyển từ A theo độ dịch chuyển \(\overrightarrow {DC} \), vật sẽ đến điểm B (do A, D, B, C tạo thành một hình chữ nhật).
Bước 2: Di chuyển tiếp tục từ B theo độ dịch chuyển \(\overrightarrow {B'C'} \)
Điểm B dịch chuyển theo \(\overrightarrow {B'C'} \) tức là di chuyển theo đoạn B'C' nhưng bắt đầu từ B. Do B và B’ nằm trên cùng một mặt phẳng, nên khi dịch chuyển từ B theo độ dịch chuyển \(\overrightarrow {B'C'} \), vật sẽ đến điểm C (do B, B', C, C' tạo thành một hình chữ nhật).
Vậy, sau khi thực hiện hai bước di chuyển, vật sẽ đến điểm C.
LT1
Trả lời câu hỏi Luyện tập 1 trang 56 SGK Toán 12 Cùng khám phá
Cho tứ diện ABCD. Chứng minh rằng \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC} \).
Phương pháp giải:
- Áp dụng quy tắc ba điểm.
- Sử dụng tính chất kết hợp và giao hoán của phép cộng vectơ.
Lời giải chi tiết:
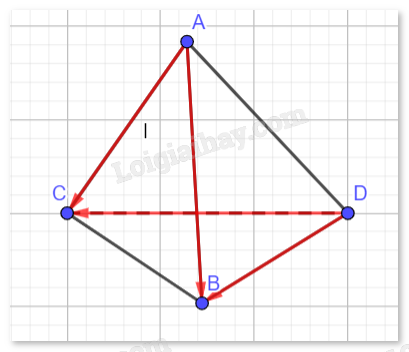
- Áp dụng quy tắc ba điểm, ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {BC} \).
- Sử dụng tính chất kết hợp và giao hoán của phép cộng vectơ, ta suy ra: \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC} \).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 56 SGK Toán 12 Cùng khám phá
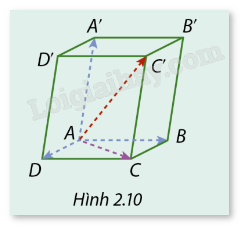
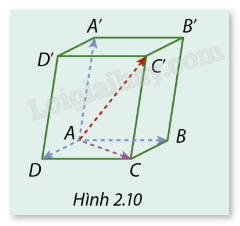
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10).
a) Tìm liên hệ giữa \(\overrightarrow {AD} + \overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Phương pháp giải:
a) Áp dụng quy tắc hình bình hành.
b) Sử dụng mối liên hệ đã chứng minh ở câu a và phép cộng của hai vectơ.
Lời giải chi tiết:
a) Trong hình hộp ABCD.A’B’C’D’ thì có đáy ABCD là hình bình hành.
Áp dụng quy tắc hình bình hành, ta được: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
b) Sử dụng phép cộng của hai vectơ, ta suy ra:
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {CC'} = \overrightarrow {AC'} \).
LT2
Trả lời câu hỏi Luyện tập 2 trang 57 SGK Toán 12 Cùng khám phá
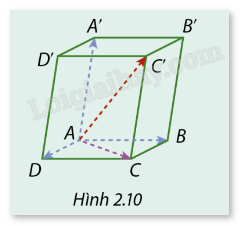
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10). Tìm vectơ \(\overrightarrow {BA} + \overrightarrow {B'C'} + \overrightarrow {DD'} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp vào hình hộp ABCD.A’B’C’D’.
Lời giải chi tiết:
Vì BB’C’C là hình chữ nhật nên \(\overrightarrow {BC} = \overrightarrow {B'C'} \).
Vì BB’D’D là hình chữ nhật nên \(\overrightarrow {D'D} = \overrightarrow {B'B} \).
Thay \(\overrightarrow {BC} = \overrightarrow {B'C'} \) và \(\overrightarrow {D'D} = \overrightarrow {B'B} \) , đồng thời áp dụng quy tắc hình hộp, ta suy ra:
\(\overrightarrow {BA} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 57 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10). Tìm tổng của vectơ \(\overrightarrow {AD} \) và vectơ đối của \(\overrightarrow {C'C} \).
Phương pháp giải:
- Sử dụng các tính chất của hình hộp.
- Xác định vectơ đối của \(\overrightarrow {C'C} \) dựa trên khái niệm: “Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).”
- Áp dụng các tính chất của phép cộng hai vectơ và quy tắc hình bình hành.
Lời giải chi tiết:
- Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên: \(\overrightarrow {C'C} = \overrightarrow {A'A} \).
- Suy ra vectơ đối của \(\overrightarrow {C'C} \) cũng là vectơ đối của \(\overrightarrow {A'A} \).
- Áp dụng các tính chất của phép cộng hai vectơ và quy tắc hình bình hành, ta suy ra: \(\overrightarrow {AD} + \left( { - \overrightarrow {C'C} } \right) = \overrightarrow {AD} + \left( { - \overrightarrow {A'A} } \right) = \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD'} \).
LT3
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
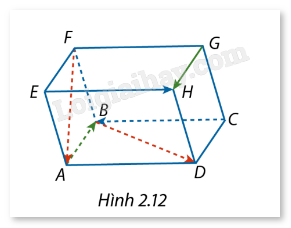
Cho hình hộp ABCD.EFGH (Hình 2.12). Hãy tìm:
a) \(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \);
b) \(\overrightarrow {FA} - \overrightarrow {BD} \).
Phương pháp giải:
1. Sử dụng tính chất của các vectơ trong hình hộp để xác định các vectơ cần tìm.
2. Áp dụng quy tắc cộng và trừ vectơ.
Lời giải chi tiết:
a) Tìm \(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \):
Ta có:
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {CB} = \overrightarrow {DA} \)
và
\(\overrightarrow {GH} = \overrightarrow {FE} ,\overrightarrow {EH} = \overrightarrow {FG} \)
Nên:
\(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} = \overrightarrow {DC} + \overrightarrow {DA} + \overrightarrow {FE} + \overrightarrow {FG} = \overrightarrow {DB} + \overrightarrow {FH} = \overrightarrow {DB} - \overrightarrow {DB} = \overrightarrow 0 \)
b) Tìm \(\overrightarrow {FA} - \overrightarrow {BD} \):
Ta có:
\(\overrightarrow {FA} = \overrightarrow {FE} + \overrightarrow {EA} \)
và
\(\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD} \)
Nên:
\(\overrightarrow {FA} - \overrightarrow {BD} = (\overrightarrow {FE} + \overrightarrow {EA} ) - (\overrightarrow {BC} + \overrightarrow {CD} )\)
Vì ABCD.EFGH là hình hộp nên ta có:\(\overrightarrow {FE} = \overrightarrow {CD} ,\overrightarrow {EA} = \overrightarrow {FB} \)
Do đó:
\(\overrightarrow {FA} - \overrightarrow {BD} = (\overrightarrow {CD} + \overrightarrow {FB} ) - (\overrightarrow {BC} + \overrightarrow {CD} ) = \overrightarrow {FB} - \overrightarrow {BC} = \overrightarrow {FB} - \overrightarrow {FG} = \overrightarrow {GB} \).
VD1
Trả lời câu hỏi Vận dụng 1 trang 58 SGK Toán 12 Cùng khám phá
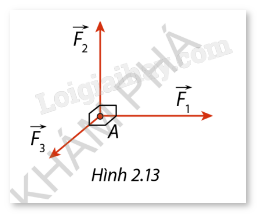
Một chất điểm chịu tác động bởi 3 lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có chung điểm đặt \(A\) và có giá vuông góc với nhau từng đôi một. Biết cường độ của các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) lần lượt là 10 N, 8 N và 5 N, xác định hợp lực của 3 lực và tính cường độ của hợp lực (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải:
- Vì các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có giá vuông góc với nhau từng đôi một, ta có thể coi chúng là các cạnh của một hình hộp chữ nhật trong không gian.
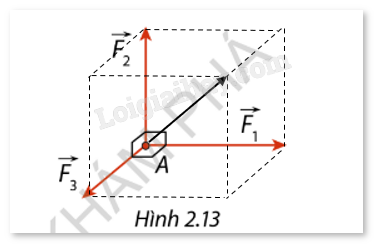
- Hợp lực \(\vec F\) của 3 lực này sẽ là đường chéo của hình hộp chữ nhật đó.
- Tính hợp lực: \(\left| {\overrightarrow F } \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + {{\left| {\overrightarrow {{F_3}} } \right|}^2}} \)
Lời giải chi tiết:
Hợp lực \(\vec F\) của 3 lực này sẽ là đường chéo của hình hộp chữ nhật tạo bởi 3 lực đó.
Xác định độ lớn của các lực:
\(|\overrightarrow {{F_1}} | = 10{\rm{N}}\)
\(|\overrightarrow {{F_2}} | = 8{\rm{N}}\)
\(|\overrightarrow {{F_3}} | = 5{\rm{N}}\)
Tính hợp lực:
\(\left| {\overrightarrow F } \right| = \sqrt {{{10}^2} + {8^2} + {5^2}} = \sqrt {189} \approx 14N\)
Vậy hợp lực của 3 lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có cường độ xấp xỉ \(14{\rm{N}}\).
- Giải mục 2 trang 58, 59, 60 SGK Toán 12 tập 1 - Cùng khám phá
- Giải mục 3 trang 60, 61, 62, 63, 64 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.3 trang 64 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.4 trang 64 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.5 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận