Giải mục 1 trang 14, 15 SGK Toán 12 tập 1 - Cánh diều

Định nghĩa

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1
LT1

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 14 SGK Toán 12 Cánh diều

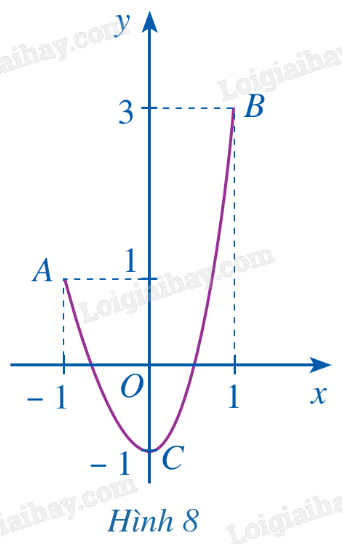
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;1} \right]\) và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:

a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất;

b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất.

Phương pháp giải:

Quan sát đồ thị và nhận xét.

Lời giải chi tiết:

a) Điểm B là điểm thuộc đồ thị hàm số có tung độ lớn nhất.

b) Điểm C là điểm thuộc đồ thị hàm số có tung độ nhỏ nhất.

LT1

Trả lời câu hỏi Luyện tập 1 trang 15 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \sqrt {9 - {x^2}} \) trên đoạn \(\left[ { - 3;3} \right]\).

Phương pháp giải:

Ứng dụng đạo hàm để tìm GTLN, GTNN.

Lời giải chi tiết:

\(f'(x) = \frac{{ - 2x}}{{2\sqrt {9 - {x^2}} }} = \frac{{ - x}}{{\sqrt {9 - {x^2}} }} = 0 \Leftrightarrow x = 0\).

Ta có \(f( - 3) = 0\); \(f(0) = 3\); \(f(3) = 0\).

Vậy \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 3 \Leftrightarrow x = 0\\\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 0 \Leftrightarrow x = \pm 3\end{array} \right.\).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 2 trang 15, 16, 17, 18 SGK Toán 12 tập 1 - Cánh diều
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm
Giải bài tập 1 trang 18 SGK Toán 12 tập 1 - Cánh diều
Nếu hàm số (y = fleft( x right)) có đạo hàm trên (mathbb{R}) thỏa mãn (f'left( x right) = sin x - 2023,forall x in mathbb{R}) thì giá trị lớn nhất của hàm số (y = fleft( x right)) trên đoạn (left[ {1;2} right]) bằng: A. (fleft( 0 right)). B. (fleft( 1 right)). C. (fleft( {1,5} right)). D. (fleft( 2 right)).
Giải bài tập 2 trang 19 SGK Toán 12 tập 1 - Cánh diều
Tìm giá trị lớn nhất của mỗi hàm số sau: a) (fleft( x right) = frac{4}{{1 + {x^2}}}). b) (fleft( x right) = x - frac{3}{x}) trên nửa khoảng ((0;3]).
Giải bài tập 3 trang 20 SGK Toán 12 tập 1 - Cánh diều
Tìm giá trị nhỏ nhất của mỗi hàm số sau: a) \(f\left( x \right) = x + \frac{4}{x}\) trên khoảng \(\left( {0; + \infty } \right)\) b) \(f\left( x \right) = {x^3} - 12x + 1\) trên khoảng \(\left( {1; + \infty } \right)\)
Giải bài tập 4 trang 19 SGK Toán 12 tập 1 - Cánh diều
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: a) (fleft( x right) = {x^3} - frac{3}{2}{x^2}) trên đoạn (left[ { - 1;2} right]) b) (fleft( x right) = {x^4} - 2{x^3} + {x^2} + 1) trên đoạn (left[ { - 1;1} right]) c) (fleft( x right) = {e^x}left( {{x^2} - 5x + 7} right)) trên đoạn (left[ {0;3} right]) d) (fleft( x right) = cos 2x + 2x + 1) trên đoạn (left[ {frac{{ - pi }}{2};pi } right])
Giải bài tập 5 trang 19 SGK Toán 12 tập 1 - Cánh diều
Trong 5s đầu tiên, một chất điểm chuyển động theo phương trình: (sleft( t right) = - {t^3} + 6{t^2} + t + 5) Trong đó t tính bằng giây và s tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?
Giải bài tập 6 trang 19 SGK Toán 12 tập 1 - Cánh diều
Người ta bơm xăng vào bình xăng của một xe ô tô. Biết thể tích V (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng t (phút) được cho bởi công thức: (Vleft( t right) = 300left( {{t^2} - {t^3}} right) + 4) với (0 le t le 0,5) a) Ban đầu trong bình xăng có bao nhiêu lít xăng ? b) Sau khi bơm 30s thì bình xăng đầy. Hỏi dung tích của bình xăng trong xe là bao nhiêu lít ? c) Khi xăng chảy vào bình xăng, gọi (V'left( t right))là tốc độ tăng thể tích tại thời điểm t với
Giải bài tập 7 trang 19 SGK Toán 12 tập 1 - Cánh diều
Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi ho được cho bởi công thức: (V = kleft( {R - r} right){r^2}) với (0 le r < R) Trong đó k là hằng số, R là bán kính bình thường của khí quan, r là bán kính khu quản khi ho. Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất ?
Giải câu hỏi mở đầu trang 14 SGK Toán 12 tập 1 - Cánh diều
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều
1. Định nghĩa Khái niệm GTLN, GTNN của hàm số