Giải bài 4 trang 93 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của (widehat {OBO'}) cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh (widehat {BOC}) và (widehat {BO'D}).

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của \(\widehat {OBO'}\) cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh \(\widehat {BOC}\) và \(\widehat {BO'D}\).

Phương pháp giải - Xem chi tiết

Chứng minh \(\widehat {OBC} = \widehat {OCB} = \widehat {CBO'} = \widehat {O'DB}\) sau đó so sánh \(\widehat {BOC}\) và \(\widehat {BO'D}\).

Lời giải chi tiết

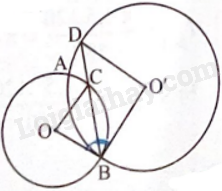
Ta có \(\widehat {OBC} = \widehat {CBO'}\) (vì BC là đường phân giác của \(\widehat {OBO'}\)).

Ta lại có \(\widehat {OBC} = \widehat {OCB}\) (vì tam giác OBC cân tại O),

\(\widehat {CBO'} = \widehat {O'DB}\) (vì tam giác O’BD cân tại O’).

Suy ra \(\widehat {OBC} = \widehat {OCB} = \widehat {CBO'} = \widehat {O'DB}\),

\(\widehat {BOC} = \widehat {BO'D}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5 trang 93 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho đường tròn (O) đường kính AB và một dây cung AP. Tia AP cắt tiếp tuyến tại B của đường tròn (O) tại T. Chứng minh rằng: a) (widehat {AOP} = 2widehat {ATB}) b) (widehat {APO} = widehat {PBT})
Giải bài 6 trang 93 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác nhọn ABC có (widehat {BAC} = {45^o}) và có các đỉnh nằm trên đường tròn (O). Các đường cao BH, CK cắt đường tròn (O) tại D, E. Chứng minh ba điểm D, O, E thẳng hàng.
Giải bài 7 trang 93 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Vòng ngoài cùng của một guồng nước có dạng đường tròn tâm O, trên đó có đánh dấu 40 điểm chia đường tròn thành 40 cung bằng nhau để gắn các gàu lấy nước. Gọi M, N là hai điểm liên tiếp và P là một điểm khác M, N trong số các điểm nói trên. Tính số đo (widehat {MON},widehat {MPN},widehat {OMN}).
Giải bài 3 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và (widehat {AMB} = {35^o}). a) Tính số đo của góc ở tâm tạo bởi hai bán kính OA, Ob. b) Tính số đo mỗi cung (oversetfrown{AB}) (cung lớn và cung nhỏ).
Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho đường tròn (O; R) và dây cung MN = (Rsqrt 3 ). Tính số đo của mỗi cung (oversetfrown{MN}) (cung lớn và cung nhỏ).
Giải bài 1 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Tìm số đo các cung nhỏ (oversetfrown{AL}), (oversetfrown{RM}) và số đo (theta ) của góc nội tiếp tương ứng trong mỗi hình sau: