-
Toán 8 tập 1 - Cánh diều
-
Toán 8 tập 2 - Cánh diều
-
Chương 6 Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương 6
-
Chương 7 Phương trình bậc nhất một ẩn
-
Chương 8 Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài tập cuối chương 8
-
Giải bài 4 trang 78 SGK Toán 8 – Cánh diều
Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P lần lượt thuộc các tia OA, OB, OC sao cho \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}} = \frac{{OC}}{{OP}} = \frac{2}{3}\). Chứng minh \(\Delta ABC \backsim\Delta MNP\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng các định lý Thales để chứng minh các tỉ số bằng nhau.
Chứng minh hai tam giác đồng dạng theo trường hợp thứ nhất.
Lời giải chi tiết
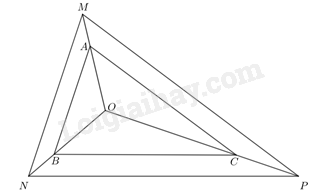
Xét tam giác MON có: \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}} = \frac{2}{3}\) nên \(AB//MN\) (Định lý Thales đảo)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{2}{3}\) (Hệ quả của định lý Thales)
Chứng minh tương tự ta được \(\frac{{BC}}{{NP}} = \frac{2}{3};\,\,\frac{{AC}}{{MP}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{AC}}{{MP}}\)
\( \Rightarrow \Delta ABC \backsim\Delta MNP\) (c-c-c)
Bình luận
Chia sẻ
- Giải bài 5 trang 78 SGK Toán 8 – Cánh diều
- Giải bài 6 trang 78 SGK Toán 8 – Cánh diều
- Giải bài 3 trang 78 SGK Toán 8 – Cánh diều
- Giải bài 2 trang 78 SGK Toán 8 – Cánh diều
- Giải bài 1 trang 78 SGK Toán 8 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
