Giải bài 4 trang 72 ôn tập chương sách bài tập toán 8 - Chân trời sáng tạo

Cho hình thang cân có độ dài hai đáy lần lượt là 10cm và 4cm, độ dài cạnh bên là 5cm. Hình thang đó có chiều cao là

Đã có lời giải SGK Toán lớp 9 - Chân trời sáng tạo (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho hình thang cân có độ dài hai đáy lần lượt là 10cm và 4cm, độ dài cạnh bên là 5cm. Hình thang đó có chiều cao là

A. 2cm.

B. 3cm.

C. 4cm.

D. 6cm.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về định lí Pythagore vào tam giác vuông để tính: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

Lời giải chi tiết

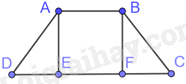
Vẽ hình thang cân ABCD có AB//CD, \(AB = 4cm,\) \(CD = 10cm\) và \(AD = BC = 5cm\)

Kẻ \(AE \bot DC,BF \bot DC\left( {E,F \in DC} \right)\) nên \(\widehat {AED} = \widehat {AEF} = \widehat {BFE} = \widehat {BFC} = {90^0}\)

Vì ABCD là hình thang cân nên \(\widehat D = \widehat C\)

Tam giác AED và tam giác BFC có:

\(\widehat {AED} = \widehat {BFC} = {90^0}\), \(\widehat D = \widehat C\), \(AD = BC = 5cm\)

Do đó, \(\Delta AED = \Delta BFC\left( {ch - gn} \right)\). Suy ra \(DE = CF\)

Tứ giác ABFE có: AB//EF, AE//BF (cùng vuông góc với DC) nên tứ giác ABFE là hình bình hành.

Do đó, \(AB = FE = 4cm\)

Suy ra: \(DE = FC = \frac{{DC - EF}}{2} = \frac{{10 - 4}}{2} = 3\left( {cm} \right)\)

Áp dụng định lí Pythagore vào tam giác ADE vuông tại E có: \(A{E^2} = A{D^2} - D{E^2} = {5^2} - {3^2} = 16\), suy ra \(AE = 4cm\)

Chọn C

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5 trang 72 ôn tập chương sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo. Biết \(MN = 6,OM = 3,ON = 4\). Độ dài của MP, NQ, PQ lần lượt là
Giải bài 6 trang 73 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình thoi EFGH có hai đường chéo cắt nhau tại O. Biết \(OE = 6,OF = 8\). Độ dài cạnh EF là
Giải bài 7 trang 73 sách bài tập toán 8 - Chân trời sáng tạo
Một hình vuông có diện tích bằng diện tích của hình chữ nhật có hai cạnh bằng 2cm và 18cm. Độ dài cạnh của hình vuông bằng
Giải bài 8 trang 73 sách bài tập toán 8 - Chân trời sáng tạo
Một hình vuông có cạnh bằng \(\sqrt 8 cm\). Độ dài đường chéo của hình vuông bằng
Giải bài 9 trang 73 sách bài tập toán 8 - Chân trời sáng tạo
Một hình bình hành có thể không có tính chất nào sau đây?
Giải bài 10 trang 73 sách bài tập toán 8 - Chân trời sáng tạo
Tính độ dài cạnh chưa biết của các tam giác vuông trong Hình 1
Giải bài 11 trang 73 sách bài tập toán 8 - Chân trời sáng tạo
Tìm số đo các góc chưa biết của các tứ giác trong Hình 2.
Giải bài 12 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho tứ giác EKIT có \(EK = ET,IK = IT,\widehat {KET} = {90^0},\widehat {EKI} = {105^0}\).
Giải bài 13 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Tính chiều cao của hình thang cân ABCD biết rằng cạnh bên \(BC = 25cm\) và các cạnh đáy \(AB = 10cm,CD = 24cm\).
Giải bài 14 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình thang cân ABCD có AB//CD, DB là tia phân giác của góc D, \(DB \bot BC\). Biết \(AB = 4cm\). Tính chu vi của hình thang đó.
Giải bài 15 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho tam giác ABC cân tại A có \(BC = 6cm\). Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
Giải bài 16 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho \(BM = DN\)
Giải bài 17 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy các điểm M, N, P, Q lần lượt là trung điểm của AO, BO, CO, DO.
Giải bài 18 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình chữ nhật ABCD có \(AB = 2BC\). Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh:
Giải bài 19 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc (widehat {ADB},widehat {DBC}left( {E in AB,K in CD} right))
Giải bài 3 trang 72 sách bài tập toán 8 - Chân trời sáng tạo
Một tứ giác có số đo ba góc lần lượt bằng \({80^0},{40^0},{100^0}\). Số đo góc còn lại bằng
Giải bài 2 trang 72 sách bài tập toán 8 - Chân trời sáng tạo
Ba số nào sau đây không thể là độ dài ba cạnh của một tam giác vuông?
Giải bài 1 trang 72 sách bài tập toán 8 - Chân trời sáng tạo
Cho tam giác MNP vuông tại M. Biết \(MN = 40,MP = 9\). Độ dài cạnh NP bằng

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.