Giải bài 34 trang 116 sách bài tập toán 9 - Cánh diều tập 1
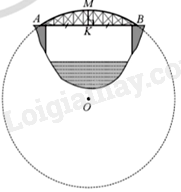
Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40m và chiều cao MK = 6m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét).
Đề bài
Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40m và chiều cao MK = 6m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Chứng minh MN là đường trung trực của AB.
Bước 2: Chứng minh \(\Delta AKM\backsim \Delta NKB(g.g)\) để tính NK.
Bước 3: Tính \(MN = 2R = MK + NK\), từ đó suy ra R.
Lời giải chi tiết
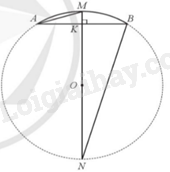
Bài toán được minh họa như hình trên. Kẻ đường kính MN của (O;R), suy ra \(O \in MN\).
Ta có \(AK = KB,MK \bot AB\) nên MK là đường trung trực của AB.
Có \(OA = OB = R\) nên O thuộc đường trung trực của AB.
Suy ra MO hay MN là đường trung trực của AB.
Do K là trung điểm của AN nên \(AK = KB = \frac{{AB}}{2} = \frac{{40}}{2} = 20\)m.
Xét tam giác AKM và tam giác NKB ta có:
\(\widehat {AKM} = \widehat {BKN} = 90^\circ \)
\(\widehat {MAK} = \widehat {MNB}\) (góc nội tiếp cùng chắn cung MB của (O))
Suy ra \(\Delta AKM\backsim \Delta NKB(g.g)\), do đó \(\frac{{AK}}{{NK}} = \frac{{MK}}{{BK}}\), hay \(NK = \frac{{AK.BK}}{{MK}} = \frac{{20.20}}{6} = \frac{{200}}{3}\)m.
Ta có \(MN = 2R = MK + NK = 6 + \frac{{200}}{3} = \frac{{213}}{3}\)m, do đó \(OM = R = \frac{{213}}{3}:2 \approx 36,3\)m.
Vậy bán kính của đường tròn chứa cung AMB khoảng 36,3m.
Bình luận
Chia sẻ
- Giải bài 35 trang 117 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 36 trang 117 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 33 trang 116 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 32 trang 116 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 31 trang 116 sách bài tập toán 9 - Cánh diều tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
