Giải bài 24 trang 92 sách bài tập toán 9 - Cánh diều tập 2

Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P (P khác C và D). Tìm phát biểu sai: A. AP = AD B. Tứ giác ABCP là hình thang cân C. (widehat {APD} = widehat {ABC}) D. (widehat {PCB} + widehat {BAP} < {180^o})

Đề bài

Cho hình bình hành ABCD. Đường tròn đi qua ba điểm A, B, C cắt cạnh CD ở P (P khác C và D). Tìm phát biểu sai:

A. AP = AD

B. Tứ giác ABCP là hình thang cân

C. \(\widehat {APD} = \widehat {ABC}\)

D. \(\widehat {PCB} + \widehat {BAP} < {180^o}\)

Phương pháp giải - Xem chi tiết

Trong một tứ giác nội tiếp, tổng hai góc đối bằng 180^o.

Lời giải chi tiết

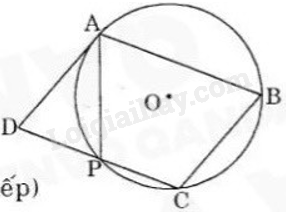
Ta có ABCD là hình bình hành suy ra \(\widehat B + \widehat C = {180^o}\) (hai góc trong cùng phía) (1)

ABCP là tứ giác nội tiếp suy ra \(\widehat B + \widehat {APC} = {180^o}\) (2)

Từ (1) và (2) suy ra \(\widehat B = \widehat {PAB}\) hay ABCP là hình thang cân.

Suy ra AP = BC (3)

mà ABCD là hình bình hành nên AD = BC (4)

Từ (3) và (4) suy ra AP = AD.

Vì ABCP nội tiếp nên \(\widehat {PCB} + \widehat {BAP} = {180^o}\).

Chọn đáp án D.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 25 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC có BC = 10 và (widehat {BAC} = {30^o}). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Giải bài 26 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tứ giác ABCD có (widehat C + widehat D = {90^o}). Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó.
Giải bài 27 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông tại A có đường cao AH = 2,4 cm và (frac{{AB}}{{AC}} = frac{3}{4}). Tính bán kính đường tròn nội tiếp r và bán kính đường tròn ngoại tiếp R của tam giác ABC.
Giải bài 28 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E. Kẻ CK vuông góc với BI. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh: a) F, E, K thẳng hàng b) K, N, M thẳng hàng.
Giải bài 29 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh: a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp. b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.
Giải bài 30 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Quan sát Hình 16. Chứng minh QR // ST.
Giải bài 31 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho lục giác đều ABCDEF cạnh bằng a. a) Chứng minh sáu điểm A, B, C, D, E, F cùng thuộc một đường tròn. Tính theo a bán kính của đường tròn đó. b) Chứng minh các tam giác ACE, BFD là các tam giác đều. Tính theo a bán kính đường tròn nội tiếp tương ứng của tam giác đó.
Giải bài 32 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = (Rsqrt 3 ) a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB. b) Tính chu vi tam giác MAB. c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất.
Giải bài 33 trang 93 sách bài tập toán 9 - Cánh diều tập 2
Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm và luôn ngoại tiếp đường tròn (I; r). Một tiếp tuyến song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Tìm độ dài BC để MN có độ dài lớn nhất.
Giải bài 23 trang 92 sách bài tập toán 9 - Cánh diều tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O), hai tia AB, DC cắt nhau tại M và (widehat {BAD} = {70^o}). Khi đó số đo góc BCM là: A. ({80^o}) B. ({70^o}) C. ({110^o}) D. ({100^o})