Giải bài 2 trang 103 sách bài tập toán 9 - Chân trời sáng tạo tập 2

Một hình quạt tròn có bán kính 29 cm, độ dài cung bằng (42pi ) cm. Người ta dùng hình quạt tròn này để tạo lập mặt xung quanh của một hình nón. Tính bán kính đáy và chiều cao của hình nón đó.

Đề bài

Một hình quạt tròn có bán kính 29 cm, độ dài cung bằng \(42\pi \) cm. Người ta dùng hình quạt tròn này để tạo lập mặt xung quanh của một hình nón. Tính bán kính đáy và chiều cao của hình nón đó.

Phương pháp giải - Xem chi tiết

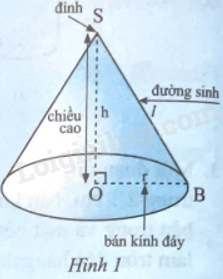
Khi quay tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón (Hình 1).

Lời giải chi tiết

Gọi r là bán kính đáy của hình tròn, độ dài cung của hình quạt bằng chu vi đáy của hình nón, khi đó: \(2\pi r = 42\pi \) suy ra r = 21 cm.

Độ dài đường sinh l của hình nón bằng bán kính của hình quạt tròn, suy ra l = 29 cm.

Chiều cao của hình nón là: h = \(\sqrt {{{29}^2} - {{21}^2}} = 20\)(cm).

Vậy bán kính đáy và chiều cao của hình nón lần lượt là 21 cm và 20 cm.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 3 trang 103 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tam giác OAB vuông tại O có AB = 37 cm, OA = 12 cm. Tính diện tích xung quanh và thể tích của hình tạo thành khi quay tam giác OAB một vòng quanh cạnh OB.
Giải bài 4 trang 103 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Một cọc tiêu có dạng hình nón bị cắt đi phần ở trên cũng có dạng hình nón như Hình 5. a) Tính diện tích xung quanh của cọc tiêu theo đơn vị in2 (không tính phần đế). b) Tính thể tích của cọc tiêu theo đơn vị in3 (không tính phần đế). (Làm tròn kết quả đến hàng đơn vị của in2, in3).
Giải bài 5 trang 103 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Để làm nón lá, người ta phải chuốt từng thanh tre mảnh, nhỏ, dẻo rồi uốn thành các vòng tròn có đường kính to nhỏ khác nhau tạo thành các vành nón. Vành lớn nhất của một chiếc nón lá có đường kính là 40 cm, khoảng cách từ đỉnh cao nhất đến một điểm trên vành này là 32 cm. Tính diện tích xung quanh của chiếc nón lá đó (kết quả làm tròn đến hàng đơn vị của xăngtimet vuông).
Giải bài 1 trang 102 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Hãy cho biết bán kính đáy, chiều cao, độ dài đường sinh của mỗi hình nó sau: