Giải bài 12 trang 128 vở thực hành Toán 8 tập 2
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
Đề bài
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ΔABE $\backsim $ ΔACF , từ đó suy ra ΔAEF $\backsim $ ΔABC
b) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF
Phương pháp giải - Xem chi tiết
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE $\backsim $ ΔACF (c.g.c)
b) Sử dụng các tỉ số đồng dạng của hai tam giác để tính EF
Lời giải chi tiết
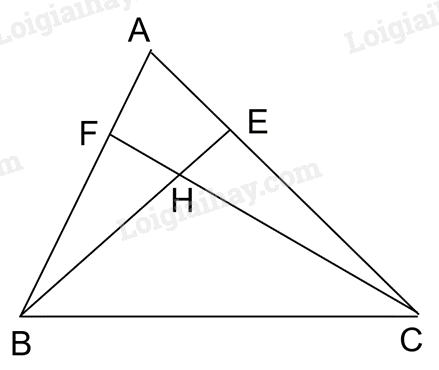
a) Khi tam giác ABC nhọn, ta có hình bên.
Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung nên ΔABE $\backsim $ ΔACF
=> $\frac{AB}{AC}=\frac{A\text{E}}{AF}$
Xét tam giác AEF và tam giác ABC có: A chung và $\frac{AB}{AC}=\frac{A\text{E}}{AF}$
=> \(\Delta AEF\backsim \Delta ABC\)(c.g.c)
Khi tam giác ABC là tam giác tù, chẳng hạn góc A tù hoặc góc B tù, tương ứng ta có hai hình sau (HS tự vẽ)
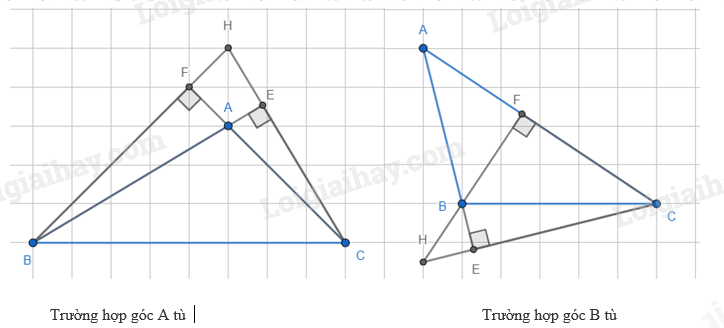
Chứng minh tương tự, ta thấy kết quả vẫn đúng.
b) Theo định lí Pythagore, trong tam giác vuông ABE, ta có:
\(A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}} \Rightarrow A{{E}^{2}}=A{{B}^{2}}-B{{E}^{2}} \\ ={{10}^{2}}-{{8}^{2}}=36\Rightarrow AE=6cm \)
Theo kết quả câu a), ta có
\(\Delta AEF\backsim \Delta ABC\Rightarrow \frac{EF}{AE}=\frac{BC}{AB}\Rightarrow EF=\frac{BC.AE}{AB}=\frac{15.6}{10}=9(cm)\)
Trả lời: EF = 9cm.
- Giải bài 13 trang 128 vở thực hành Toán 8 tập 2
- Giải bài 14 trang 129 vở thực hành Toán 8 tập 2
- Giải bài 15 trang 130 vở thực hành Toán 8 tập 2
- Giải bài 11 trang 127 vở thực hành Toán 8 tập 2
- Giải bài 10 trang 126 vở thực hành Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay













Danh sách bình luận