Giải bài 1 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo

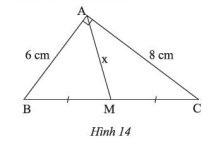
Cho Hình 14

Đã có lời giải SGK Toán lớp 9 - Chân trời sáng tạo (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho Hình 14. Tìm \(x\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng ĐL Pythagore vào tam giác vuông \(ABC\)

Lời giải chi tiết

Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại \(A\), ta có:

\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100 = {10^2}\)

Suy ra \(BC = 10\) (cm).

Xét \(\Delta ABC\) vuông tại \(A\) có \(AM\) là đường trung tuyến ứng với cạnh huyền nên \(AM\) bằng nửa cạnh huyền \(BC\).

Do đó \(x = AM = \frac{1}{2}BC = \frac{1}{2}.10 = 5\) (cm)

Vậy \(x = 5\) cm

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 5 phiếu

Bài tiếp theo

Giải bài 2 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho Hình 15. Vẽ thêm điểm
Giải bài 3 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho tam giác
Giải bài 4 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho tam giác
Giải bài 5 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Lấy một tờ giấy, gấp làm tư để có một góc vuông
Giải mục 2 trang 84, 85, 86 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho tứ giác
Giải mục 1 trang 82, 83, 84 SGK Toán 8 tập 1– Chân trời sáng tạo
Dùng thước đo góc để đo số đo các góc
Lý thuyết Hình chữ nhật - Hình vuông SGK Toán 8 - Chân trời sáng tạo
Hình chữ nhật là gì?

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.