Đề thi vào 10 môn Toán TP Hồ Chí Minh năm 2025

Đề bài

Bài 1. (1,5 điểm) Cho hàm số \(y = \frac{{{x^2}}}{2}\) có đồ thị \(\left( P \right)\).

a) Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ.

b) Tìm tọa độ các điểm thuộc \(\left( P \right)\) có tung độ bằng 18.

Bài 2. (1,0 điểm) Cho phương trình \(2{x^2} - 7x + 4 = 0\).

a) Chứng minh phương trình trên có hai nghiệm phân biệt \({x_1},{x_2}\).

b) Không giải phương trình, hãy tính giá trị của biểu thức \(A = {x_1}\left( {3{x_2} + {x_1}} \right) + x_2^2\).

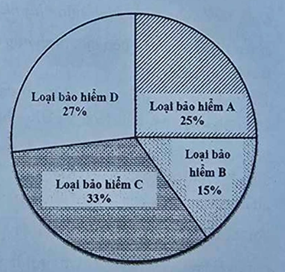
Bài 3. (1,5 điểm) Biểu đồ tròn cho biết tỉ lệ về số lượng các loại bảo hiểm đã bán được trong tháng 4/2025 của một công ty. Biết rằng trong tháng này, công ty đã bán được 300 gói bảo hiểm các loại cho 300 khách hàng khác nhau.

a) Tính số lượng cụ thể của mỗi loại bảo hiểm mà công ty đã bán được trong tháng 4/2025?

b) Bộ phận chăm sóc khách hàng chọn ngẫu nhiên một khách hàng đã mua bảo hiểm của công ty trong tháng 4/2025 để khảo sát. Tính xác suất của biến cố: "Khách hàng được chọn không mua loại bảo hiểm B".

Bài 4. (1,0 điểm) Một khu vườn hình chữ nhật có chiều dài là \(2x\) (m) và chiều rộng là \(x\) (m), \(x > 4\). Bác Ba làm một lối đi quanh khu vườn rộng 2 mét như hình vẽ. Phần đất còn lại (phần in đậm) dùng để trồng hoa.

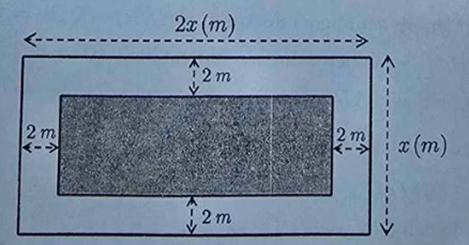
a) Viết biểu thức theo \(x\) biểu diễn diện tích phần đất dùng để trồng hoa và thu gọn biểu thức đó.

b) Giả sử diện tích phần đất trồng hoa là \(4800{m^2}\). Tính chiều dài và chiều rộng của khu vườn.

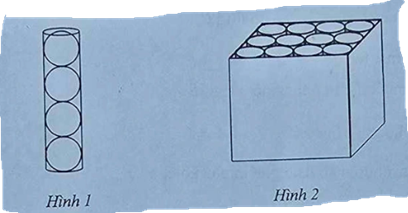
Bài 5. (1,0 điểm) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít 4 quả bóng tennis có dạng hình cầu như Hình 1. Biết diện tích bề mặt mỗi quả bóng tennis là \(132,67\left( {c{m^2}} \right)\).

a) Tính bán kính của mỗi quả bóng tennis.

b) Nhà sản xuất thường sử dụng các thùng giấy hình hộp chữ nhật (có nắp) để chứa 12 hộp tennis sao cho các hộp tennis được xếp vừa khít trong thùng giấy như Hình 2. Hỏi cần tối thiểu bao nhiêu \({m^2}\) giấy để thiết kế một thùng như trên (giả sử các mép nối không đáng kể).

Các kết quả được làm tròn đến hàng phần trăm.

Cho biết diện tích bề mặt hình cầu là \(S = 4\pi {R^2}\) với \(R\) là bán kính hình cầu. Diện tích toàn phần hình hộp chữ nhật là \({S_{tp}} = 2\left( {ab + bc + ca} \right)\) với \(a,b,c\) lần lượt là chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật.

Bài 6. (1,0 điểm) Từ vị trí \(A\) của một công viên có dạng hình vuông \(ABCD\) cạnh \(a\left( {km} \right)\), hai bạn Hòa và Bình bắt đầu chạy bộ cùng lúc với vận tốc không đổi dọc theo các cạnh của hình vuông và theo hai hướng khác nhau. Biết rằng, hai bạn gặp nhau lần thứ nhất tại vị trí \(E\) cách \(A\) một khoảng bằng \(1km\) và gặp lại nhau lần thứ hai tại vị trí \(F\) cách \(A\) một khoảng bằng \(0,4km\) như hình vẽ. Gọi \(x,y\left( {km/h} \right)\) lần lượt là vận tốc của Hòa và Bình.

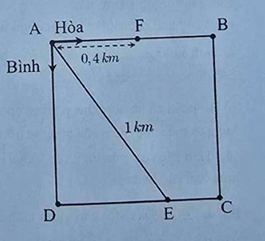
a) Chứng minh rằng \(\frac{x}{y} = \frac{{AB + BC + CE}}{{AD + DE}}\).

b) Tìm giá trị của \(a\).

Bài 7. (3,0 điểm) Từ một điểm \(A\) nằm ngoài đường tròn \(\left( {O;R} \right)\) với \(OA = 2R\), kẻ hai tiếp tuyến \(AB,AC\) đến đường tròn \((B,C\) là các tiếp điểm). Vẽ đường kính \(BD\) của đường tròn \(\left( O \right)\). Gọi \(E\) là giao điểm thứ hai của đường thẳng \(AD\) với \(\left( O \right)\). Đường thẳng \(BC\) và \(AO\) cắt nhau tại \(H\).

a) Chứng minh rằng tam giác \(BED\) vuông và \(ABHE\) là tứ giác nội tiếp.

b) Chứng minh rằng \(O{D^2} = OH.OA\) và \(\angle HDO = \angle HBE\).

c) Tính theo \(R\) chu vi và diện tích tam giác \(DHE\).

----- HẾT -----

Lời giải

Bài 1. (1,5 điểm) Cho hàm số \(y = \frac{{{x^2}}}{2}\) có đồ thị \(\left( P \right)\).

a) Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ.

b) Tìm tọa độ các điểm thuộc \(\left( P \right)\) có tung độ bằng 18.

Lời giải:

a)

Ta có bảng giá trị sau:

\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm

\(O\left( {0;0} \right);A\left( { - 2;2} \right);B\left( { - 1;\frac{1}{2}} \right);C\left( {1;\frac{1}{2}} \right);D\left( {2;2} \right)\)

Hệ số \(a = \frac{1}{2} > 0\) nên parabol có bề lõm hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số \(y = \frac{{{x^2}}}{2}\) như sau:

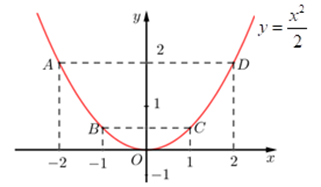
b)

Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm thuộc (P). Khi đó \(M\left( {{x_M};\frac{1}{2}x_M^2} \right)\).

Giả sử M có tung độ bằng 18.

Ta có \(\frac{1}{2}x_M^2 = 18\)

\(x_M^2 = 36\)

\(\left| {{x_M}} \right| = 6\).

Có hai giá trị thỏa mãn là \({x_M} = 6;{x_M} =  - 6\).

Vậy các điểm thuộc (P) có tung độ bằng 18 có tọa độ là (6;18), (-6;18).

Bài 2. (1,0 điểm) Cho phương trình \(2{x^2} - 7x + 4 = 0\).

a) Chứng minh phương trình trên có hai nghiệm phân biệt \({x_1},{x_2}\).

b) Không giải phương trình, hãy tính giá trị của biểu thức \(A = {x_1}\left( {3{x_2} + {x_1}} \right) + x_2^2\).

Lời giải:

a)

Phương trình bậc hai \(2{x^2} - 7x + 4 = 0\) có \(a = 2;b =  - 7,c = 4\)

Ta có \(\Delta  = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.2.4 = 17 > 0\) nên phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\)

b)

Do phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\) nên áp dụng hệ thức Viète ta có

\(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{7}{2}}\\{{x_1}{x_2} = \frac{4}{2} = 2}\end{array}} \right.\)

Khi đó \(A = {x_1}\left( {3{x_2} + {x_1}} \right) + x_2^2\)

\( = 3{x_1}{x_2} + x_1^2 + x_2^2\)

\( = {x_1}{x_2} + \left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right)\)

\( = {x_1}{x_2} + {\left( {{x_1} + {x_2}} \right)^2}\)

\( = 2 + {\left( {\frac{7}{2}} \right)^2} = 2 + \frac{{49}}{4} = \frac{{8 + 49}}{4} = \frac{{57}}{4}\)

Vậy \(A = \frac{{57}}{4}\)

Bài 3. (1,5 điểm) Biểu đồ tròn cho biết tỉ lệ về số lượng các loại bảo hiểm đã bán được trong tháng 4/2025 của một công ty. Biết rằng trong tháng này, công ty đã bán được 300 gói bảo hiểm các loại cho 300 khách hàng khác nhau.

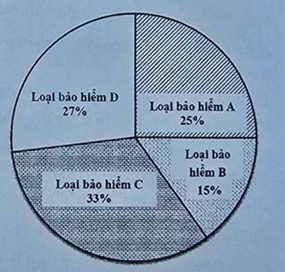
a) Tính số lượng cụ thể của mỗi loại bảo hiểm mà công ty đã bán được trong tháng 4/2025?

b) Bộ phận chăm sóc khách hàng chọn ngẫu nhiên một khách hàng đã mua bảo hiểm của công ty trong tháng 4/2025 để khảo sát. Tính xác suất của biến cố: "Khách hàng được chọn không mua loại bảo hiểm B".

Lời giải:

a)

Số lượng bảo hiểm loại A mà công ty đã bán được là: \(300.25{\rm{\% }} = 75\) (gói)

Số lượng bảo hiểm loại B mà công ty đã bán được là: \(300.15{\rm{\% }} = 45\) (gói)

Số lượng bảo hiểm loại C mà công ty đã bán được là: \(300.33{\rm{\% }} = 99\) (gói)

Số lượng bảo hiểm loại D mà công ty đã bán được là: \(300.27{\rm{\% }} = 81\) (gói)

Vậy số lượng bảo hiểm loại A, B, C, D mà công ty đã bán được trong tháng 4/2025 lần lượt là 75 gói, 45 gói, 99 gói, 81 gói.

b)

Có 300 kết quả có thể khi chọn ngẫu nhiên một khách hàng đã mua bảo hiểm của công ty trong tháng 4/2025.

Số kết quả thuận lợi cho biến cố: “Khách hàng được chọn không mua loại bảo hiểm B" là: \(75 + 99 + 81 = 255\) (kết quả)

Xác suất của biến cố “Khách hàng được chọn không mua loại bảo hiểm B” là:

\(\frac{{255}}{{300}} = \frac{{17}}{{20}}\)

Vậy xác suất của biến cố “Khách hàng được chọn không mua loại bảo hiểm B” là \(\frac{{17}}{{20}}\).

Bài 4. (1,0 điểm) Một khu vườn hình chữ nhật có chiều dài là \(2x\) (m) và chiều rộng là \(x\) (m), \(x > 4\). Bác Ba làm một lối đi quanh khu vườn rộng 2 mét như hình vẽ. Phần đất còn lại (phần in đậm) dùng để trồng hoa.

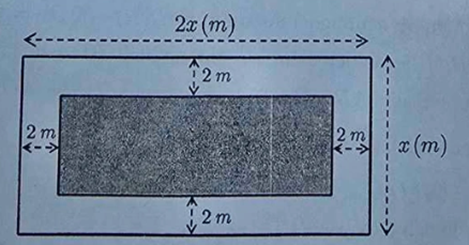
a) Viết biểu thức theo \(x\) biểu diễn diện tích phần đất dùng để trồng hoa và thu gọn biểu thức đó.

b) Giả sử diện tích phần đất trồng hoa là \(4800{m^2}\). Tính chiều dài và chiều rộng của khu vườn.

Lời giải:

a)

Chiều rộng của phần đất dùng để trồng hoa là \(x - 2.2 = x - 4\) (m)

Chiều dài của phần đất dùng để trồng hoa là \(2x - 2.2 = 2x - 4\) (m)

Diện tích phần đất dùng để trồng hoa là \(S = \left( {x - 4} \right)\left( {2x - 4} \right)\) (\({m^2}\))

Thu gọn biểu thức S:

\(\left( {x - 4} \right)\left( {2x - 4} \right)\)

\( = 2{x^2} - 4x - 8x + 16\)

\( = 2{x^2} - 12x + 16\)

Vậy biểu thức biểu diễn diện tích phần đất dùng để trồng hoa là \(S = 2{x^2} - 12x + 16\) (\({m^2}\)).

b)

Diện tích phần đất trồng hoa là \(4800{m^2}\) nên ta có \(2{x^2} - 12x + 16 = 4800\).

Giải phương trình:

\(2{x^2} - 12x + 16 = 4800\)

\({x^2} - 6x + 8 = 2400\)

\({x^2} - 6x - 2392 = 0\)

Ta có \(\Delta  = {\left( { - 6} \right)^2} - 4.1.\left( { - 2392} \right) = 36 + 9568 = 9604 > 0\) nên phương trình có 2 nghiệm phân biệt:

\({x_1} = \frac{{6 + \sqrt {9604} }}{2} = \frac{{6 + 98}}{2} = 52\) (thỏa mãn điều kiện)

\({x_2} = \frac{{6 - \sqrt {9604} }}{2} = \frac{{6 - 98}}{2} =  - 46{\rm{\;}}\) (loại)

Vậy chiều rộng của khu vườn là 52 m, chiều dài của khu vườn là \(2.52 = 104\) m.

Bài 5. (1,0 điểm) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít 4 quả bóng tennis có dạng hình cầu như Hình 1. Biết diện tích bề mặt mỗi quả bóng tennis là \(132,67\left( {c{m^2}} \right)\).

a) Tính bán kính của mỗi quả bóng tennis.

b) Nhà sản xuất thường sử dụng các thùng giấy hình hộp chữ nhật (có nắp) để chứa 12 hộp tennis sao cho các hộp tennis được xếp vừa khít trong thùng giấy như Hình 2. Hỏi cần tối thiểu bao nhiêu \({m^2}\) giấy để thiết kế một thùng như trên (giả sử các mép nối không đáng kể).

Các kết quả được làm tròn đến hàng phần trăm.

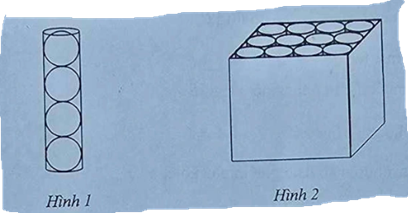
Cho biết diện tích bề mặt hình cầu là \(S = 4\pi {R^2}\) với \(R\) là bán kính hình cầu. Diện tích toàn phần hình hộp chữ nhật là \({S_{tp}} = 2\left( {ab + bc + ca} \right)\) với \(a,b,c\) lần lượt là chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật.

Lời giải:

a)

Vì diện tích bề mặt mỗi quả bóng tennis là \(132,67c{m^2}\) nên \(4\pi {R^2} = 132,67\)

Suy ra \({R^2} \approx \frac{{132,67}}{{4\pi }} \approx 10,56\)

Do đó \(R \approx \sqrt {10,56}  \approx 3,25\) (cm)

Vậy bán kính mỗi quả bóng tennis khoảng 3,25cm.

b)

Mỗi hộp tennis chứa 4 quả tennis nên chiều cao của hộp tennis là:

\(4.2R = 4.2.3,25 = 26\left( {cm} \right)\)

Đường kính đáy một hộp tennis là: \(2R = 2.3,25 = 6,5\left( {cm} \right)\).

Vì thùng giấy chứa được 12 hộp tennis (3x4) nên

chiều dài thùng giấy là: \(6,5.4 = 26\left( {cm} \right)\);

chiều rộng của thùng giấy là: \(6,5.3 = 19,5\left( {cm} \right)\);

chiều cao của thùng giấy chính là chiều cao của hộp tennis nên chiều cao của thùng giấy là 26cm

Diện tích giấy để thiết kế một thùng (diện tích toàn phần của hình hộp chữ nhật) là:

\({S_{tp}} = 2\left( {ab + bc + ca} \right) \approx 2\left( {26.19,5 + 19,5.26 + 26.26} \right) = 2\left( {507 + 507 + 676} \right) = 2\left( {1690} \right) = 3380\left( {c{m^2}} \right)\)

\( = 0,338\left( {{m^2}} \right) \approx 0,34\left( {{m^2}} \right)\)

Vậy cần tối thiểu \(0,34{m^2}\) giấy để thiết kế một thùng như trên.

Bài 6. (1,0 điểm) Từ vị trí \(A\) của một công viên có dạng hình vuông \(ABCD\) cạnh \(a\left( {km} \right)\), hai bạn Hòa và Bình bắt đầu chạy bộ cùng lúc với vận tốc không đổi dọc theo các cạnh của hình vuông và theo hai hướng khác nhau. Biết rằng, hai bạn gặp nhau lần thứ nhất tại vị trí \(E\) cách \(A\) một khoảng bằng \(1km\) và gặp lại nhau lần thứ hai tại vị trí \(F\) cách \(A\) một khoảng bằng \(0,4km\) như hình vẽ. Gọi \(x,y\left( {km/h} \right)\) lần lượt là vận tốc của Hòa và Bình.

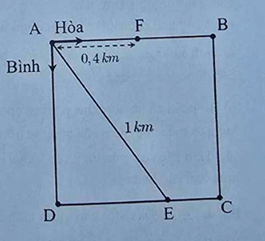
a) Chứng minh rằng \(\frac{x}{y} = \frac{{AB + BC + CE}}{{AD + DE}}\).

b) Tìm giá trị của \(a\).

Lời giải:

a) Ta có \(\Delta ADE\) vuông tại D nên \(DE = \sqrt {A{E^2} - A{D^2}}  = \sqrt {{1^2} - {a^2}}  = \sqrt {1 - {a^2}} \) và

\(CE = DC - DE = a - \sqrt {1 - {a^2}} \)

Tại lần gặp nhau đầu tiên bạn Bình đi được quãng đường là \(AD + DE = a + \sqrt {1 - {a^2}} \)

Hoà đi được quãng đường là \(AB + BC + EC = a + a + a - \sqrt {1 - {a^2}}  = 3a - \sqrt {1 - {a^2}} \)

Do thời gian 2 bạn đi từ lúc xuất phát đến khi gặp nhau là như nhau nên quãng đường đi của Hoà và Bình tỉ lệ thuận với vận tốc đi tương ứng của hai bạn.

b)

Tại lần gặp thứ hai ở F thì Bình đi quãng đường là

\(AD + DC + BC + BF = a + a + a + \left( {a - 0,4} \right) = 4a - 0,4\)

b) Hoà đi quãng đường là \(AB + BC + CD + DA + AF = a + a + a + a + 0,4 = 4a + 0,4\)

Khi đó ta có phương trình \({\rm{\;}}\frac{{3a - \sqrt {1 - {a^2}} }}{{a + \sqrt {1 - {a^2}} }} = \frac{{4a + 0,4}}{{4a - 0,4}}\)

\({\rm{Suy\;ra}}\) \({\rm{\;}}\frac{{3a - \sqrt {1 - {a^2}} }}{{4a + 0,4}} = \frac{{a + \sqrt {1 - {a^2}} }}{{4a - 0,4}}\)

Do \(a > 0\) nên áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{{3a - \sqrt {1 - {a^2}} }}{{4a + 0,4}} = \frac{{a + \sqrt {1 - {a^2}} }}{{4a - 0,4}} = \frac{{\left( {3a - \sqrt {1 - {a^2}} } \right) + \left( {a + \sqrt {1 - {a^2}} } \right)}}{{\left( {4a + 0,4} \right) + \left( {4a - 0,4} \right)}} = \frac{{4a}}{{8a}} = \frac{1}{2}\)

Suy ra \({\rm{\;}}\frac{{3a - \sqrt {1 - {a^2}} }}{{4a + 0,4}} = \frac{1}{2}\)

\(2\left( {3a - \sqrt {1 - {a^2}} } \right) = 4a + 0,4\)

\(6a - 2\sqrt {1 - {a^2}}  = 4a + 0,4\)

\(2a - 0,4 = 2\sqrt {1 - {a^2}} \)

\(\sqrt {1 - {a^2}}  = a - 0,2\)

Suy ra \({\rm{\;}}1 - {a^2} = {\left( {a - 0,2} \right)^2}{\rm{\;}}\) với \({\rm{(}}a > 0,2)\)

\(1 - {a^2} = {a^2} - 0,4a + 0,04\)

\(2{a^2} - 0,4a - 0,96 = 0\)

Giải phương trình ta được \(a = 0,8\) (thoả mãn) hoặc \(a =  - 0,6\) (không thoả mãn)

Vậy \(a = 0,8\) km

Bài 7. (3,0 điểm) Từ một điểm \(A\) nằm ngoài đường tròn \(\left( {O;R} \right)\) với \(OA = 2R\), kẻ hai tiếp tuyến \(AB,AC\) đến đường tròn \((B,C\) là các tiếp điểm). Vẽ đường kính \(BD\) của đường tròn \(\left( O \right)\). Gọi \(E\) là giao điểm thứ hai của đường thẳng \(AD\) với \(\left( O \right)\). Đường thẳng \(BC\) và \(AO\) cắt nhau tại \(H\).

a) Chứng minh rằng tam giác \(BED\) vuông và \(ABHE\) là tứ giác nội tiếp.

b) Chứng minh rằng \(O{D^2} = OH.OA\) và \(\angle HDO = \angle HBE\).

c) Tính theo \(R\) chu vi và diện tích tam giác \(DHE\).

Lời giải:

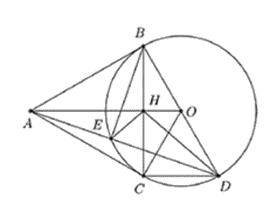
a)

Vì tam giác BED nội tiếp đường tròn đường kính BD nên tam giác BED vuông tại E

Khi đó $\angle BED=90{}^\circ $

Do đó tam giác ABE vuông tại E

Suy ra A, B, E cùng thuộc đường tròn đường kính AB (1)

Ta có: $AB = AC$ (tính chất hai tiếp tuyến cắt nhau) $OB = OC$ (bán kính)

Suy ra AO là đường trung trực của BC tại trung điểm H của BC

Do đó $\Delta AHB$ vuông tại H

Nên A, H, B cùng thuộc đường tròn đường kính AB (2)

Từ (1) và (2) ta có A, E, H, B cùng thuộc đường tròn đường kính AB

Vậy tứ giác ABHE nội tiếp

b) Xét $\Delta OBH$ và $\Delta OAB$ có:

$\angle BOA$ chung

$\angle OHB=\angle OBA=90{}^\circ $

suy ra $\Delta OBH \backsim \Delta OAB(\text{g}\text{.g)}$ nên $\dfrac{OB}{OA} = \dfrac{OH}{OB}$ suy ra $OB^{2} = OH.OA$

mà $OD = OB$ nên $OD^{2} = OH.OA$

Suy ra $\dfrac{OD}{OH} = \dfrac{OA}{OD}$

Mà $\angle AOD$ chung nên $\Delta ODH \backsim \Delta OAD\text{(c}\text{.g}\text{.c)}$

Suy ra $\angle HDO = \angle HAD$

Mà $\angle \text{HAD=}\angle \text{HBE}\ $ (ABHE nội tiếp) nên $\angle HDO = \angle HBE$

c) Áp dụng định lí Pythagore cho tam giác ABO vuông tại B ta có

$AB = \sqrt{AO^{2} - OB^{2}} = \sqrt{\left( {2R} \right)^{2} - R^{2}} = \sqrt{4R^{2} - R^{2}} = \sqrt{3R^{2}} = R\sqrt{3}$

Áp dụng định lí Pythagore cho tam giác ABD vuông tại B ta có

$AD = \sqrt{AB^{2} + BD^{2}} = \sqrt{\left( {R\sqrt{3}} \right)^{2} + \left( {2R} \right)^{2}} = \sqrt{3R^{2} + 4R^{2}} = \sqrt{7R^{2}} = R\sqrt{7}$

Ta có $\Delta ABH \backsim \Delta AOB$ (g.g) nên $AH.AO = AB^{2}$

Suy ra $AH = \dfrac{AB^{2}}{AO} = \dfrac{\left( {R\sqrt{3}} \right)^{2}}{2R} = \dfrac{3R^{2}}{2R} = \dfrac{3R}{2}$

Xét $\Delta ABE$ và $\Delta ADB$ có

$\angle AEB=\angle ABD=90{}^\circ $

$\angle BAD$ chung

Suy ra $\Delta ABE \backsim \Delta ADB\text{~(g}\text{.g)}$

Do đó $\angle ABE = \angle ADB$

Mà $\angle ABE = \angle AHE$ nên $\angle AHE = \angle ADB$

Mặt khác $\angle HAE$ chung suy ra $\Delta AHE \backsim \Delta ADO$ (g.g)

Do đó $\dfrac{HE}{DO} = \dfrac{AH}{AD}$ hay $HE = \dfrac{AH.DO}{AD} = \dfrac{\dfrac{3R}{2}.R}{R\sqrt{7}} = \dfrac{\dfrac{3R^{2}}{2}}{R\sqrt{7}} = \dfrac{3R}{2\sqrt{7}} = \dfrac{3R\sqrt{7}}{14}$

Vì $\Delta ODH \backsim \Delta OAD$ nên $\dfrac{DH}{OD} = \dfrac{OD}{OA}\ $, suy ra $DH = \dfrac{OD^{2}}{OA} = \dfrac{R^{2}}{2R} = \dfrac{R}{2}$

Vì $\Delta DBE \backsim \Delta ADAB\text{(g}\text{.g)}$ nên $\dfrac{DE}{DB} = \dfrac{DB}{DA}$, suy ra $DE = \dfrac{DB^{2}}{DA} = \dfrac{\left( {2R} \right)^{2}}{R\sqrt{7}} = \dfrac{4R^{2}}{R\sqrt{7}} = \dfrac{4R}{\sqrt{7}} = \dfrac{4R\sqrt{7}}{7}$

Chu vi tam giác HED là:

$\begin{array}{l} {HE + HD + DE} \\ {= \dfrac{3R\sqrt{7}}{14} + \dfrac{R\sqrt{7}}{2} + \dfrac{4R\sqrt{7}}{7}} \\ {= \dfrac{3R\sqrt{7} + 7R\sqrt{7} + 8R\sqrt{7}}{14}} \\ {= \dfrac{18R\sqrt{7}}{14} = \dfrac{9R\sqrt{7}}{7}} \end{array}$

Ta có:

$\begin{array}{l} {S_{ABD} = \dfrac{1}{2}AB.BD = \dfrac{1}{2}R\sqrt{3}.2R = R^{2}\sqrt{3},} \\ {S_{AOD} = \dfrac{1}{2}S_{ABD} = \dfrac{1}{2}R^{2}\sqrt{3}} \end{array}$

Vì $\Delta AHE \backsim \Delta ADO$ nên $\ \dfrac{S_{AHE}}{S_{ADO}} = \left( \dfrac{AH}{AD} \right)^{2} = \left( \dfrac{\dfrac{3R}{2}}{R\sqrt{7}} \right)^{2} = \left( \dfrac{3}{2\sqrt{7}} \right)^{2} = \dfrac{9}{4.7} = \dfrac{9}{28}$

Vì $\Delta ODH \backsim \Delta OAD\ $ nên $\dfrac{S_{ODH}}{S_{OAD}} = \left( \dfrac{OD}{OA} \right)^{2} = \left( \dfrac{R}{2R} \right)^{2} = \left( \dfrac{1}{2} \right)^{2} = \dfrac{1}{4}$

Khi đó

$S_{DHE} = S_{AOD} - S_{AHE} - S_{OHD}$

$= S_{AOD} - \dfrac{9}{28}S_{AOD} - \dfrac{1}{4}S_{AOD} = \dfrac{3}{7}S_{AOD}$

$= \dfrac{3}{7}.\dfrac{1}{2}R^{2}\sqrt{3} = \dfrac{3R^{2}\sqrt{3}}{14}$

Vậy chu vi, diện tích tam giác DEH lần lượt là $\dfrac{9R\sqrt{7}}{7},\dfrac{3R^{2}\sqrt{3}}{14}$.