Đề thi minh hoạ vào 10 môn Toán TP Hồ Chí Minh năm 2025

Đề bài

Câu 1: Cho hàm số \(y = \frac{{{x^2}}}{2}\)

a) Vẽ đồ thị (P) của hàm số trên.

b) Tìm những điểm M thuộc (P) có tung độ và hoành độ bằng nhau.

Câu 2: Cho phương trình \(2{x^2} - 5x + 1 = 0\)

a) Chứng minh phương trình trên có hai nghiệm phân biệt.

b) Không giải phương trình, hãy tính giá trị của biểu thức

Câu 3: Biên độ nhiệt là khoảng cách chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất trong cùng một khoảng thời gian nhất định (một ngày, một tháng, một năm,…) của cùng một vùng địa lí. Biểu đồ cột kép dưới đây biểu diễn nhiệt độ (độ C) các ngày trong một tuần tại Thành phố Hồ Chí Minh.

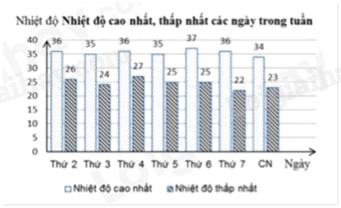
a) Trong tuần này, ngày có biên độ nhiệt lớn nhất của thành phố Hồ Chí Minh là thứ mấy?

b) Chọn ngẫu nhiên một ngày trong tuần, tính xác suất của các biến cố sau:

A: “Ngày được chọn có nhiệt độ cao nhất không quá 35 độ C”.

B: “Ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C”.

Câu 4: Một khu vườn hình chữ nhật (phần in đậm) có chiều dài và chiều rộng lần lượt là 70m và 30m. Người ta dự tính mở rộng thêm khu vườn bằng cách cải tạo thêm \(X\) (mét) về phía ngoài của chiều dài và chiều rộng khu vườn như hình vẽ.

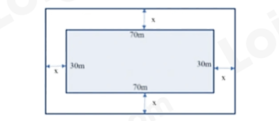
a) Viết biểu thức S biểu diễn theo \(X\) diện tích của khu vườn hình chữ nhật sau khi mở rộng.

b) Biết rằng sau khi mở rộng thì diện tích của khu vườn lớn hơn diện tích ban đầu \(\;1150{\mkern 1mu} {m^2}\).

Tìm giá trị của \(X\) (làm tròn đến hàng phần muời của mét).

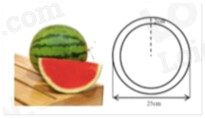
Câu 5: Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính 25cm và phần vỏ dày 2cm.

a) Coi phần ruột màu đỏ cũng có dạng hình cầu có cùng tâm với quả dưa hấu. Tính thể tích phần ruột quả dưa hấu.

(Kết quả làm tròn đến hàng phần trăm của \(c{m^3}\))

b) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng \(80\% \) thể tích phần ruột. Nước ép dưa hấu sẽ được đựng trong các ly thuỷ tinh giống nhau, phần lòng trong dạng hình trụ có chiều cao $10cm$ và đường kính đáy lòng trong là $5cm.$ Mỗi ly chỉ chứa \(70\% \) thể tích. Hỏi để đựng nước ép của quả dưa hấu nói trên thì cần ít nhất bao nhiêu cái ly?

Biết công thức thể tích hình trụ là \(V = p{R^2}h\) (R là bán hính đáy; h là chiều cao); công thức tính thể tích hình cầu là \(V = \frac{4}{3}p{R^3}.\)

Câu 6: Thép không gỉ Ferritic là họ thép hợp kim có chứa từ 12 đến 27 phần trăm crôm. Một nhà máy luyện thép hiện có sẵn một lượng hợp kim thép chứa \(10\% \) crôm và một lượng hợp kim thép chứa \(30\% \) crôm. Giả sử trong quá trình luyện thép các nguyên liệu không bị hao hụt.

a) Tính khối lượng hợp kim thép mỗi loại từ hai loại thép trên dùng để luyện được 500 tấn thép chứa \(16\% \) crôm.

b) Nhà máy dự định luyện ra loại thép không gỉ Ferritic từ 100 tấn thép chứa \(10\% \) crôm và \(x\) tấn thép chứa \(30\% \) crôm. Hỏi \(x\) nằm trong khoảng nào?

Câu 7: Cho tam giác ABC có ba góc nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt hai cạnh AB, AC lần lượt tại E và F (E khác B, F khác C). Các đoạn thẳng BF và CE cắt nhau tại H, tia AH cắt BC tại K.

a) Chứng minh \(\angle BEC = \angle BFC = {90^0}\), từ đó suy ra tứ giác AEHF nội tiếp.

b) Gọi D là giao điểm của AH và (O) (D nằm giữa A và H), chứng minh \(B{D^2} = BK \cdot BC\) và \(\angle BDH = \angle BFD\)

c) Trong trường hợp góc \(BAC = {60^0}\) và \(BC = 6\;{\rm{cm}}\), tính độ dài đoạn thẳng EF và bán kính đường tròn ngoại tiếp tam giác AEF.

----- HẾT -----

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM.COM

Câu 1 (TH):

Cách giải:

a) Vẽ đồ thị (P) của hàm số trên.

Ta có bảng giá trị sau:

Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0;0} \right);A\left( { - 4;8} \right);B\left( { - 2;2} \right);A'\left( {4;8} \right);B'\left( {2;2} \right)\).

Ta được đồ thị hàm số \(y = \frac{{{x^2}}}{2}\) như sau:

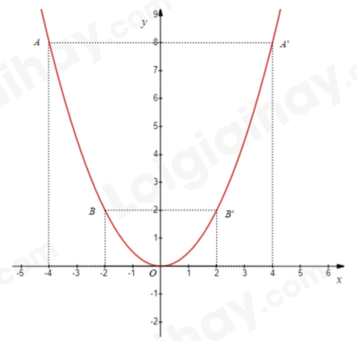
b) Tìm những điểm M thuộc (P) có tung độ và hoành độ bằng nhau.

Điểm có tung độ và hoành độ bằng nhau có dạng \(M\left( {{x_0};{x_0}} \right)\) thì \({x_0} = \frac{{{x_0}^2}}{2}\)

Suy ra \({x_0}^2 = 2{x_0}\)

\(\begin{array}{*{20}{l}}{{x_0}^2 - 2{x_0} = 0}\\{{x_0}\left( {{x_0} - 2} \right) = 0}\end{array}\)

\({x_0} = 0\) và \({x_0} = 2\)

Vậy những điểm M thuộc (P) có tung độ và hoành độ bằng nhau là \(M\left( {0;0} \right)\) và \(M\left( {2;2} \right)\).

Câu 2 (TH):

Cách giải:

a) Chứng minh phương trình trên có hai nghiệm phân biệt.

Phương trình \(2{x^2} - 5x + 1 = 0\) có \(a = 2;b = {\rm{ \;}} - 5;c = 1\) nên ta có:

\(\Delta {\rm{ \;}} = {\left( { - 5} \right)^2} - 4.2.1 = 25 - 8 = 17 > 0\) nên phương trình có hai nghiệm phân biệt.

b) Không giải phương trình, hãy tính giá trị của biểu thức \(A = {x_1}({x_1} + 2024) + {x_2}\left( {{x_2} + 2025} \right) - {x_2}\)

Áp dụng định lí Viète, ta có:

\(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{5}{2}}\\{{x_1}{x_2} = \frac{1}{2}}\end{array}} \right.\)

Ta có: \(A = {x_1}({x_1} + 2024) + {x_2}\left( {{x_2} + 2025} \right) - {x_2}\)

\(A = {x_1}^2 + 2024{x_1} + {x_2}^2 + 2025{x_2} - {x_2}\)

\(\begin{array}{*{20}{l}}{A = \left( {{x_1}^2 + 2{x_1}{x_2} + {x_2}^2} \right) - 2{x_1}{x_2} + \left( {2024{x_1} + 2024{x_2}} \right)}\\{A = {{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + 2024\left( {{x_1} + {x_2}} \right)}\\{A = {{\left( {\frac{5}{2}} \right)}^2} - 2.\frac{1}{2} + 2024.\frac{5}{2}}\\{A = \frac{{20261}}{4}}\end{array}\)

Vậy \(A = \frac{{20261}}{4}\).

Câu 3 (TH):

Cách giải:

a) Dựa vào biểu đồ cột kép, ta có biên độ nhiệt của các ngày trong tuần là:

Thứ 2: \(36 - 26 = 10\), thứ 3: \(35 - 24 = 11\), thứ 4: \(36 - 27 = 9\); thứ 5: \(35 - 25 = 10\);

Thứ 6: \(37 - 25 = 12\); thứ 7: \(36 - 22 = 14\); chủ nhật: \(34 - 23 = 11.\)

Vậy ngày có biên độ nhiệt lớn nhất trong tuần của thành phố Hồ Chí Minh là thứ 7.

b) Ta có số ngày có nhiệt độ cao không quá 35 độ C là 3 (ngày).

Suy ra số phần tử của biến cố A là 3.

Xác suất để ngày được chọn có nhiệt độ cao nhất không quá 35 độ C là \(\frac{3}{7}\).

Có số ngày có biên độ nhiệt nhỏ hơn 12 độ C là 5 (ngày).

Suy ra số phần tử của biến cố B là 5.

Xác suất để ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C là \(\frac{5}{7}\).

Câu 4 (VD):

Cách giải:

a) Viết biểu thức S biểu diễn theo \(X\) diện tích của khu vườn hình chữ nhật sau khi mở rộng.

Chiều rộng của khu vườn hình chữ nhật sau khi mở rộng là:

\(30 + X + X = 30 + 2X{\mkern 1mu} {\mkern 1mu} (m)\)

Chiều dài của khu vườn hình chữ nhật sau khi mở rộng là:

\(70 + X + X = 70 + 2X{\mkern 1mu} {\mkern 1mu} (m)\)

Diện tích của khu vườn hình chữ nhật sau khi mở rộng là:

\((30 + 2X).(70 + 2X){\mkern 1mu} {\mkern 1mu} ({m^2})\)

b) Biết rằng sau khi mở rộng thì diện tích của khu vườn lớn hơn diện tích ban đầu \(\;1150{\mkern 1mu} {m^2}\).

Tìm giá trị của \(X\) (làm tròn đến hàng phần muời của mét).

ĐKXĐ: \(X > 0\)

Diện tích của khu vườn ban đầu là: 70.30 = 2100 (m²)

Vì sau khi mở rộng thì diện tích của khu vườn lớn hơn diện tích ban đầu \(\;1150{\mkern 1mu} {m^2}\) nên ta có phương trình:

\((30 + 2X).(70 + 2X) = 2100 + 1150 = 3250\)

\(2100 + 60X + 140X + 4{X^2} = 3250\)

\(4{X^2} + 200X - 1150 = 0\)

\(4{X^2} + 200X - 1150 = 0\)

Ta có \(\Delta ' = 14600 > 0\) nên phương trình có hai nghiệm phân biệt:

\({X_1} \approx 5,2{\mkern 1mu} {\mkern 1mu} (tm);{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {X_2} \approx {\rm{ \;}} - 55,2{\mkern 1mu} {\mkern 1mu} (l)\)

Vậy giá trị của X là khoảng 5,2 m.

Câu 5 (VD):

Cách giải:

a) Bán kính của phần ruột quả dưa hấu là: \(\frac{{25 - 2.2}}{2} = 10,5\left( {cm} \right)\)

Thể tích phần ruột của quả dưa hấu là:

\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .10,{5^3} \approx 4849,05\left( {c{m^3}} \right)\)

b) Thể tích nước ép dưa hấu là: \({V_n} = 80\% .4849,05 = 3879,24\left( {c{m^3}} \right)\)

Thể tích của phần đựng nước ly thuỷ tinh là: \({V_l} = 70\% .\pi {R^2}h = 70\% .\pi .{\left( {\frac{5}{2}} \right)^2}.10 \approx 137,44\left( {c{m^3}} \right)\)

Ta có: \(\frac{{{V_n}}}{{{V_l}}} = \frac{{3879,24}}{{137,44}} \approx 28,22\)

Do đó cần ít nhất 29 cái ly để đựng hết nước ép của quả dưa hấu.

Câu 6 (VD):

Cách giải:

a) Tính khối lượng hợp kim thép mỗi loại từ hai loại thép trên dùng để luyện được 500 tấn thép chứa \(16\% \) crôm.

Gọi a là số tấn hợp kim thép chứa 10% crom cần dùng (a > 0)

Khi đó, 500 – a là số tấn hợp kim thép 30% cần dùng.

Ta có:

a.10% + (500 – a).30% = 500.16%

10a + (500 – a).30 = 500.16

a = 350 (TMĐK)

Vậy số hợp kim thép chứa 10% crom cần dùng là 350 tấn, số hợp kim thép chứa 30% cần dùng là 150 tấn.

b) Nhà máy dự định luyện ra loại thép không gỉ Ferritic từ 100 tấn thép chứa \(10\% \) crôm và \(x\) tấn thép chứa \(30\% \) crôm. Hỏi \(x\) nằm trong khoảng nào?

Ta có số crôm từ 100 tấn thép chứa \(10\% \) crôm là \(10\% .100 = 10\) (tấn)

Số crôm từ \(x\) tấn thép chứa \(30\% \) crom: $0,3x$ (tấn)

Tổng số tấn thép là \(100 + x\) (tấn)

Phần trăm crôm có trong tổng số tấn thép nhà máy dự định luyện ra là: \(\frac{{10 + 0,3x}}{{100 + x}}.100\)

Theo đầu bài, thép không gỉ Ferritic có chứa từ 12 đến 27 phần trăm crôm, ta có:

\(\begin{array}{*{20}{l}}{12 \le \frac{{10 + 0,3x}}{{100 + x}}.100 \le 27}\\{1200 + 12x \le 1000 + 30x \le 2700 + 27x}\\{\left\{ {\begin{array}{*{20}{l}}{1200 + 12x \le 1000 + 30x}\\{1000 + 30x \le 2700 + 27x}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{18x \ge 200}\\{3x \le 1700}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x \ge \frac{{100}}{9}}\\{x \le \frac{{1700}}{3}}\end{array}} \right.}\\{\frac{{100}}{9} \le x \le \frac{{1700}}{3}}\end{array}\)

Vậy x nằm trong khoảng từ \(\frac{{100}}{9}\) đến \(\frac{{1700}}{3}\)

Câu 7 (VD):

Cách giải:

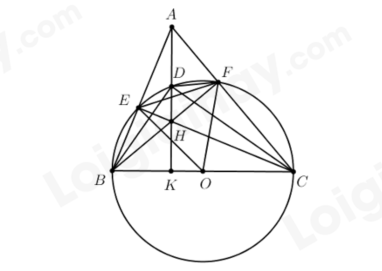
a) Ta có  (tính chất góc nội tiếp chắn nửa đường tròn)

Khi đó \(\Delta AEH\) vuông tại E nên A,E,H cùng thuộc đường tròn đường kính AH

Tương tự \(\Delta AFH\) vuông tại F nên A,H,F cùng thuộc đường tròn đường kính AH

Vậy A, E, F, H cùng thuộc đường trong đường kính AH hay tứ giác AEHF nội tiếp.

b) Ta có  (tính chất góc nội tiếp chắn nửa đường tròn)

Xét \(\Delta BDK\) và \(\Delta BCD\) có

\(\angle CBD\) chung

\(\angle BKD = \angle BDC\left( { = {{90}^0}} \right)\)

Nên $\Delta BDK\backsim \Delta BCD\left( g.g \right)$

Suy ra \(\frac{{BD}}{{BC}} = \frac{{BK}}{{BD}}\) hay \(B{D^2} = BK.BC\)

Do $\Delta BDK\backsim \Delta BCD\left( g.g \right)$ nên \(\angle BDH = \angle BCD\) (hai góc tương ứng)

Mà \(\angle BCD = \angle BFD\) (hai góc nội tiếp cùng chắn cung BD)

Nên \(\angle BDH = \angle BFD\) (đpcm)

c) Do \(\Delta AFB\) vuông tại F  nên \(\angle ABF = {90^0} - \angle BAF = {90^0} - {60^0} = {30^0}\)

Mà   nên \(\angle EOF = {2.30^0} = {60^0}\)

Xét \(\Delta OEF\) cân tại O (do \(OE = OF\)) có \(\angle EOF = {60^0}\) nên \(\Delta OEF\) là tam giác đều

Suy ra \(EF = OE = OF = \frac{1}{2}BC = 3\)cm.

Xét \(\Delta ABC\) có đường cao CE và BF cắt nhau tại H nên H là trực tâm

Suy ra \(AH \bot BC\)

Xét \(\Delta AHF\) và \(\angle BHK\) có \(\angle AHF = \angle BHK\) (đối đỉnh) và \(\angle AFH = \angle BKH\left( { = {{90}^0}} \right)\)

Suy ra \(\angle HAF = \angle HBK\) hay \(\angle HAF = \angle FBC\)

Kết hợp \(\angle AFH = \angle BFC\left( { = {{90}^0}} \right)\) suy ra $\Delta AFH\backsim \Delta BFC\left( g.g \right)$ 

Suy ra  \(\frac{{AH}}{{BC}} = \frac{{AF}}{{BF}} = \cot \angle FAB = \cot {60^0} = \frac{{\sqrt 3 }}{3}\)

Suy ra \(AH = \frac{{\sqrt 3 }}{3}BC = \frac{{\sqrt 3 }}{3}.6 = 2\sqrt 3 \)

Xét tứ giác AEHF nội tiếp đường tròn đường kính AH nên bán kính bằng \(\frac{{2\sqrt 3 }}{2} = \sqrt 3 \).