Đề thi vào 10 môn Toán Bình Dương năm 2025

Đề bài

I. TRẮC NGHIỆM:

II. TRẮC NGHIỆM ĐÚNG SAI:

III. TỰ LUẬN:

Câu 15: (1 điểm) Giải phương trình \({x^2} - 5x + 6 = 0\).

Câu 16: (1 điểm) Rút gọn biểu thức \(P = \frac{{\sqrt {x + 2\sqrt x  + 1} }}{{x - 1}}.\sqrt {x - 2\sqrt x  + 1} \) với \(x > 1\).

Câu 17: (1 điểm) Một trang trại trồng dưa hấu để phục vụ trong dịp Tết Nguyên đán. Đến mùa thu hoạch, muốn ước tính năng suất của vụ thu hoạch, chủ trang trại đem cân ngẫu nhiên 40 quả dưa hấu. Kết quả thu được như bảng sau (đơn vị tính kilogram)

a) Lập bảng tần số cho mẫu số liệu trên.

b) Giá trị nào có tần số lớn nhất? Tính tần số tương đối của giá trị đó.

Câu 18: (2 điểm) Cho tam giác ABC vuông tại A. Vẽ đường tròn (I) đường kính AB và đường tròn (K) đường kính AC. Gọi D là giao điểm khác A của đường tròn (I) và đường tròn (K).

a) Chứng minh rằng D nằm trên cạnh huyền BC của tam giác ABC.

b) Chứng minh rằng tứ giác AIDK nội tiếp được một đường tròn.

-------- Hết --------

Lời giải

I. TRẮC NGHIỆM:

II. TRẮC NGHIỆM ĐÚNG SAI:

III. TỰ LUẬN: 

Câu 15: (1 điểm) Giải phương trình \({x^2} - 5x + 6 = 0\).

Lời giải:

Ta có \(\Delta  = {( - 5)^2} - 4.1.6 = 1 > 0\) nên phương trình có hai nghiệm phân biệt:

\({x_1} = \frac{{5 + 1}}{2} = 3;\,\,{x_2} = \frac{{5 - 1}}{2} = 2\)

Vậy phương trình có hai nghiệm \(x = 3\) và \(x = 2\)

Câu 16: (1 điểm) Rút gọn biểu thức \(P = \frac{{\sqrt {x + 2\sqrt x  + 1} }}{{x - 1}}.\sqrt {x - 2\sqrt x  + 1} \) với \(x > 1\).

Lời giải:

ĐK: \(x > 1\)

\(\begin{array}{l}P = \frac{{\sqrt {x + 2\sqrt x  + 1} }}{{x - 1}}.\sqrt {x - 2\sqrt x  + 1} \\ = \frac{{\sqrt {{{\left( {\sqrt x  + 1} \right)}^2}} }}{{x - 1}}.\sqrt {{{\left( {\sqrt x  - 1} \right)}^2}} \end{array}\)

\( = \frac{{\left| {\sqrt x  + 1} \right|}}{{x - 1}}.\left| {\sqrt x  - 1} \right|\)

\( = \frac{{\sqrt x  + 1}}{{x - 1}}.\left( {\sqrt x  - 1} \right)\) (với \(x > 1\))

\(\begin{array}{l} = \frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{x - 1}}\\ = \frac{{x - 1}}{{x - 1}}\\ = 1\end{array}\)

Vậy \(P = 1\).

Câu 17: (1 điểm) Một trang trại trồng dưa hấu để phục vụ trong dịp Tết Nguyên đán. Đến mùa thu hoạch, muốn ước tính năng suất của vụ thu hoạch, chủ trang trại đem cân ngẫu nhiên 40 quả dưa hấu. Kết quả thu được như bảng sau (đơn vị tính kilogram)

a) Lập bảng tần số cho mẫu số liệu trên.

b) Giá trị nào có tần số lớn nhất? Tính tần số tương đối của giá trị đó.

Lời giải:

a) Ta có bảng tần số:

b) Giá trị có tần số lớn nhất là 2,5 (kilogram), với tần số \(m = 12.\)

Tần số tương đối của 2,5 là \(\frac{{12}}{{40}}.100\% = 30\%.\)

Câu 18: (2 điểm) Cho tam giác ABC vuông tại A. Vẽ đường tròn (I) đường kính AB và đường tròn (K) đường kính AC. Gọi D là giao điểm khác A của đường tròn (I) và đường tròn (K).

a) Chứng minh rằng D nằm trên cạnh huyền BC của tam giác ABC.

b) Chứng minh rằng tứ giác AIDK nội tiếp được một đường tròn.

Lời giải:

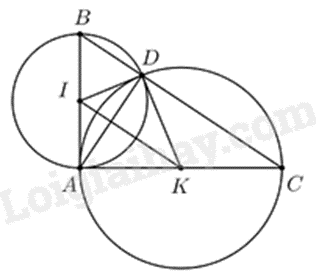
Do \(\Delta ABD\) có A, B, D cùng thuộc (I) và AB là đường kính nên \(\Delta ABD\) vuông tại D

Suy ra \(BD \bot AD\) (1)

Tương tự \(\Delta ADC\) có A, D, C cùng thuộc (K) và AC là đường kính nên \(\Delta ADC\) vuông tại D

Suy ra \(CD \bot AD\) (2)

Từ (1) và (2) suy ra B, D, C thẳng hàng

Vậy D nằm trên cạnh huyền BC của tam giác ABC.

b) Xét \(\Delta AIK\) và \(\Delta DIK\) có

\(IA = ID\) (cùng bằng bán kính của (I))

\(KA = KD\) (cùng bằng bán kính của (K))

\(IK\) là cạnh chung

Suy ra \(\Delta AIK = \Delta DIK\left( {c.c.c} \right)\)

Suy ra \(\angle IAK = \angle IDK = {90^0}\). Khi đó \(\Delta DIK\) vuông tại D

Ta có \(\Delta AIK\) vuông tại A nên A, I, K cùng thuộc đường tròn đường kính IK

   \(\Delta DIK\) vuông tại D nên D, I, K cùng thuộc đường tròn đường kính IK

Vậy A, I, D, K cùng thuộc đường tròn đường kính IK

Chứng tỏ AIDK nội tiếp được một đường tròn. (đpcm)