Đề thi vào 10 môn Toán Bình Dương năm 2020

Đề bài

Bài 1  (2,0 điểm)

Giải các phương trình, hệ phương trình sau:

     1) ${x^2} + x - 12 = 0$                                                                 $2)\,{x^4} + 8{x^2} - 9 = 0$

Bài 2 (1,5 điểm)

Cho phương trình: ${x^2} - 2020x + 2021 = 0$ có hai nghiệm phân biệt ${x_1},\,{x_2}$. Không giải phương trình, tính giá trị của các biểu thức sau:

     $1)\,\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}}$                                                                           $2)\,x_1^2 + x_2^2$

Bài 3 (1,5 điểm)

Cho Parabol $\left( P \right):\,y = \dfrac{3}{2}{x^2}$ và đường thẳng $\left( d \right):\,y =  - \dfrac{3}{2}x + 3$

     1) Vẽ đồ thị của $\left( P \right)$ và $\left( d \right)$ trên cùng một mặt phẳng tọa độ.

     2) Tìm tọa độ các giao điểm của $\left( P \right)$ và $\left( d \right)$ bằng phép tính.

Bài 4 (1,5 điểm)

Cho biểu thức $A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{x\sqrt x  - 2x + \sqrt x }}$ với $0 < x \ne 1$.

     1) Rút gọn biểu thức $A.$

     2) Tính giá trị của biểu thức $A$ khi $x = 8 - 2\sqrt 7 .$

Bài 5 (3,5 điểm)

Cho đường tròn $\left( {O;3cm} \right)$ có đường kính $AB$ và tiếp tuyến $Ax$. Trên $Ax$ lấy điểm $C$ sao cho $AC = 8cm,\,BC$ cắt đường tròn $\left( O \right)$ tại $D.$ Đường phân giác của góc $CAD$ cắt đường tròn $\left( O \right)$ tại $M$ và cắt $BC$ tại $N.$

     1) Tính độ dài đoạn thẳng $AD$.

2) Gọi $E$là giao điểm của $AD$ và $MB$. Chứng minh tứ giác $MNDE$ nội tiếp được trong đường tròn.

3) Chứng minh tam giác $ABN$ là tam giác cân.

4) Kẻ $EF$ vuông góc với $AB$ ($F$ thuộc $AB$). Chứng minh: $N,E,F$ thẳng hàng.

Lời giải chi tiết

Bài 1 - Ôn tập tổng hợp chương 2, 3, 4 - Đại số

Phương pháp:

1) Giải phương trình bằng cách đưa về phương trình tích.

2) Giải phương trình bằng cách đặt ẩn phụ:

Đặt $t = {x^2}\,\,\left( {t \ge 0} \right)$, phương trình đã cho trở thành: ${t^2} + 8t - 9 = 0$

Nhẩm nghiệm để giải phương trình ẩn $t$ từ đó suy ra nghiệm $x.$

3) Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

1) ${x^2} + x - 12 = 0$

$\begin{array}{l} \Leftrightarrow {x^2} - 3x + 4x - 12 = 0\\ \Leftrightarrow \left( {{x^2} - 3x} \right) + \left( {4x - 12} \right) = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 4\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 4\end{array} \right.\end{array}$

Vậy tập nghiệm của phương trình là $S = \left\{ {3; - 4} \right\}$.

2) ${x^4} + 8{x^2} - 9 = 0$

Đặt $t = {x^2}\,\,\left( {t \ge 0} \right)$, phương trình đã cho trở thành: ${t^2} + 8t - 9 = 0$.

Nhận thấy $a + b + c = 1 + 8 + \left( { - 9} \right) = 0$ nên phương trình ${t^2} + 8t - 9 = 0$ có nghiệm $t = 1\,\,\left( {tm} \right)$, $t = \dfrac{c}{a} =  - 9\,\,\left( {ktm} \right)$.

Với $t = 1$ ta có ${x^2} = 1 \Leftrightarrow x =  \pm 1$.

Vậy tập nghiệm của phương trình là $S = \left\{ { \pm 1} \right\}$.

3) $\left\{ \begin{array}{l}3x + y =  - 1\\6x + y = 2\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}6x + 2y =  - 2\\6x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y =  - 4\\3x + y =  - 1\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}y =  - 4\\3x - 4 =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y =  - 4\\3x = 3\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}y =  - 4\\x = 1\end{array} \right.$.

Vậy nghiệm của hệ phương trình là $\left( {x;y} \right) = \left( {1; - 4} \right)$.

Bài 2 - Hệ thức Vi-ét và ứng dụng

Phương pháp:

Tính $\Delta ' = {b^{'2}} - ac > 0$ chứng minh phương trình đã cho có hai nghiệm phân biệt ${x_1},\,\,{x_2}.$

Áp dụng định lý Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2020\\{x_1}{x_2} = 2021\end{array} \right.$

Từ đó biến đổi và tính giá trị của các biểu thức bài cho.

Cách giải:

Xét phương trình: ${x^2} - 2020x + 2021 = 0\,\,\,\left( * \right)$

Ta có: $\Delta ' = {1010^2} - 2021 = 1018079 > 0$

$\Rightarrow$ Phương trình $\left( * \right)$ có hai nghiệm phân biệt ${x_1},\,\,{x_2}$

Áp dụng định lý Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2020\\{x_1}{x_2} = 2021\end{array} \right.$

a) $\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}}$

Ta có:  $\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \dfrac{{2020}}{{2021}}.$

b) $x_1^2 + x_2^2$

Ta có: $x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}$ $= {2020^2} - 2.2021 = 4076358$

Bài 3 - Ôn tập tổng hợp chương 2, 3, 4 - Đại số

Phương pháp:

1) Lập bảng giá trị, vẽ đồ thị các hàm số trên cùng hệ trục tọa độ.

2) Giải phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm.

Thế hoành độ giao điểm vào một trong hai hàm số đã cho, để tìm tung độ giao điểm của hai đồ thị hàm số.

Cách giải:

Cho parabol $\left( P \right):\,\,\,y = \dfrac{3}{2}{x^2}$ và đường thẳng $\left( d \right):\,\,\,y =  - \dfrac{3}{2}x + 3$

1) Vẽ đồ thị của $\left( P \right)$ và $\left( d \right)$ trên cùng một mặt phẳng tọa độ.

+) Vẽ parabol $\left( P \right):\,\,y = \dfrac{3}{2}{x^2}$

Ta có bảng giá trị:

Vậy $\left( P \right):\,\,y = \dfrac{3}{2}{x^2}$ là đường cong đi qua các điểm: $\left( { - 2;\,\,6} \right),\,\,\left( { - 1;\,\,\dfrac{3}{2}} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,\dfrac{3}{2}} \right),\,\,\left( {2;\,\,6} \right).$

+) Vẽ $\left( d \right):\,\,y =  - \dfrac{3}{2}x + 3$

Ta có bảng giá trị:

Vậy $\left( d \right):\,\,\,y =  - \dfrac{3}{2}x + 3$ là đường thẳng đi qua các điểm $\left( {0;\,\,3} \right)$ và $\left( {2;\,\,0} \right).$

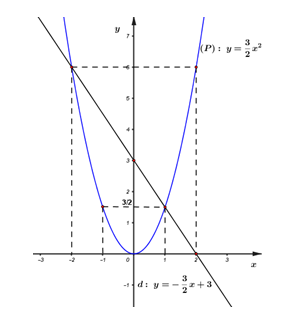
2) Tìm tọa độ giao điểm của $\left( P \right)$ và $\left( d \right)$ bằng phép tính.

Xét phương trình hoành độ giao điểm của $\left( P \right)$ và $\left( d \right)$ ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{3}{2}{x^2} =  - \dfrac{3}{2}x + 3\\ \Leftrightarrow 3{x^2} =  - 3x + 6\\ \Leftrightarrow 3{x^2} + 3x - 6 = 0\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 2\\x = 1\end{array} \right.\end{array}$

+) Với $x =  - 2$ $\Rightarrow y = \dfrac{3}{2}.{\left( { - 2} \right)^2} = 6$ $\Rightarrow A\left( { - 2;\,\,6} \right).$

+) Với $x = 1$ $\Rightarrow y = \dfrac{3}{2}{.1^2} = \dfrac{3}{2}$ $\Rightarrow B\left( {1;\,\,\dfrac{3}{2}} \right)$

Vậy $\left( d \right)$ cắt $\left( P \right)$ tại hai điểm phân biệt $A\left( { - 2;\,\,6} \right)$ và $B\left( {1;\,\,\dfrac{3}{2}} \right).$

Bài 4 - Ôn tập chương 1: Căn bậc hai. Căn bậc ba

Phương pháp:

1) Quy đồng mẫu, biến đổi và rút gọn biểu thức đã cho.

2) Biến đổi $x,$ đối chiếu với ĐKXĐ rồi thay vào biểu thức đã rút gọn để tính giá trị của biểu thức đã cho.

Cách giải:

$A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{x\sqrt x  - 2x + \sqrt x }}$ với $0 < x \ne 1$.

1) Rút gọn biểu thức $A$.

$A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{x\sqrt x  - 2x + \sqrt x }}$ với $0 < x \ne 1$.

$\begin{array}{l}A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{x\sqrt x  - 2x + \sqrt x }}\\A = \left( {\dfrac{1}{{\sqrt x \left( {\sqrt x  - 1} \right)}} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{\sqrt x \left( {x - 2\sqrt x  + 1} \right)}}\\A = \dfrac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}}:\dfrac{{\sqrt x  + 1}}{{\sqrt x {{\left( {\sqrt x  - 1} \right)}^2}}}\\A = \dfrac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}}.\dfrac{{\sqrt x {{\left( {\sqrt x  - 1} \right)}^2}}}{{\sqrt x  + 1}}\\A = \sqrt x  - 1\end{array}$

2) Tính giá trị của biểu thức $A$ khi $x = 8 - 2\sqrt 7$.

Điều kiện: $0 < x \ne 1.$

Ta có:

$\begin{array}{l}x = 8 - 2\sqrt 7 \\x = {\left( {\sqrt 7 } \right)^2} - 2.\sqrt 7 .1 + {1^2}\\x = {\left( {\sqrt 7  - 1} \right)^2}\\ \Rightarrow \sqrt x  = \sqrt {{{\left( {\sqrt 7  - 1} \right)}^2}}  = \left| {\sqrt 7  - 1} \right| = \sqrt 7  - 1\,\,\left( {Do\,\,\sqrt 7  - 1 > 0} \right)\end{array}$

Thay $\sqrt x  = \sqrt 7  - 1\,\,\left( {tm\,\,DKXD} \right)$ vào biểu thức A sau khi rút gọn ta có:

$A = \sqrt 7  - 1 - 1 = \sqrt 7  - 2$.

Vậy khi $x = 8 - 2\sqrt 7$ thì $A = \sqrt 7  - 2$.

Bài 5 - Ôn tập tổng hợp chương 1, 2, 3 - Hình học

Phương pháp:

1) Tính độ dài đoạn thẳng $AD$ bằng hệ thức lượng trong tam giác $CAB$ vuông tại $A$ có đường cao $AD.$

2) Chứng minh tứ giác nội tiếp bằng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối diện bằng ${180^0}.$

3) Chứng minh tam giác $ABN$ cân dựa vào tính chất của tam giác cân.

4) Áp dụng tiên đề Ơ-clit để chứng minh ba điểm $N,\,\,E,\,\,F$ thẳng hàng.

Cách giải:

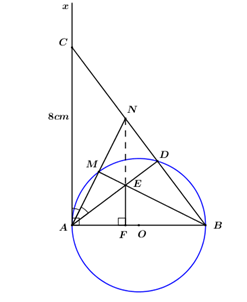
1) Tính độ dài đoạn thẳng $AD$.

Vì $\angle ADB$ nội tiếp chắn nửa đường tròn $\left( O \right)$ nên $\angle ADB = {90^0}$ $\Rightarrow AD \bot BD$ hay $AD \bot BC$.

Ta có: $Ax$ là tiếp tuyến của $\left( O \right)$ tại $A$ nên $Ax \bot AB$ hay $AB \bot AC$.

            $AB$ là đường kính của $\left( {O;3cm} \right)$ nên $AB = 2.3 = 6\,\,\left( {cm} \right)$.

Do đó tam giác $ABC$ vuông tại $A$ có đường cao $AD$.

Áp dụng hệ thức lượng trong tam giác vuông $ABC$ ta có:

$\begin{array}{l}\,\,\,\,\,\dfrac{1}{{A{D^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Rightarrow \dfrac{1}{{A{D^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{8^2}}}\\ \Rightarrow \dfrac{1}{{A{D^2}}} = \dfrac{{25}}{{576}} \Rightarrow A{D^2} = \dfrac{{675}}{{25}}\\ \Rightarrow AD = \dfrac{{24}}{5} = 4,8\,\,\left( {cm} \right)\end{array}$ 

Vậy $AD = 4,8\,\,cm$.

2) Gọi $E$ là giao điểm của $AD$ và $MB$. Chứng minh rằng tứ giác $MNDE$ nội tiếp được trong đường tròn.

Ta có: $AD \bot BC\,\,\left( {cmt} \right) \Rightarrow \angle EDN = {90^0}$.

Tương tự ta có: $\angle AMB$ là góc nội tiếp chắn nửa đường tròn $\left( O \right)$ nên $\angle AMB = {90^0}$

$\Rightarrow AM \bot BM$ hay $AN \bot BM$.

$\Rightarrow \angle EMN = {90^0}$.

Xét tứ giác $MNDE$ có $\angle EDN + \angle EMN = {90^0} + {90^0} = {180^0}$.

Vậy tứ giác $MNDE$ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng ${180^0}$).

3) Chứng minh tam giác $ABN$ là tam giác cân.

Ta có: $\angle CAN = \angle ABM$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $AM$).

          $\angle MAD = \angle MBD$ (hai góc nội tiếp cùng chắn cung $MD$).

Mà $\angle CAN = \angle MAD$ (gt) $\Rightarrow \angle ABM = \angle MBD$, do đó $BM$ là tia phân giác của $\angle ABN$.

Xét tam giác $ABN$ có $BM$ là đường cao đồng thời là đường phân giác nên tam giác $ABN$ cân tại $B$  (đpcm).

4) Kẻ $EF$ vuông góc với $AB$ ($F$ thuộc $AB$). Chứng minh: $N,\,\,E,\,\,F$ thẳng hàng.

Xét tam giác $ABN$ có:

$\begin{array}{l}AD \bot BN\,\,\left( {cmt} \right)\\BM \bot AN\,\,\left( {cmt} \right)\\AD \cap BM = \left\{ E \right\}\,\,\left( {gt} \right)\end{array}$

$\Rightarrow E$ là trực tâm của tam giác $ABN$.

Do đó $NE$ là đường cao thứ ba của tam giác $ABN$ nên $NE \bot AB$.

Lại có $EF \bot AB\,\,\left( {gt} \right)$.

$\Rightarrow$ Qua điểm $E$ nằm ngoài đường thẳng $AB$ kẻ được hai đường thẳng $EF,\,\,NE$ cùng vuông góc với $AB$.

$\Rightarrow NE \equiv EF$ (Tiên đề Ơ-clit).

Vậy $N,\,\,E,\,\,F$ thẳng hàng (đpcm).