Đề thi minh hoạ vào 10 môn Toán Ninh Bình năm 2025
Tải vềCăn bậc hai của 16 là A. (sqrt 4 ) và ( - sqrt 4 ) B. (4) C. ( - 4) D. (4) và ( - 4)
Đề bài
Phần I: Trắc nghiệm
Câu 1: Căn bậc hai của 16 là
A. \(\sqrt 4 \) và \( - \sqrt 4 \)
B. \(4\)
C. \( - 4\)
D. \(4\) và \( - 4\)
Câu 2: Kết quả của phép tính \(\sqrt 2 .\sqrt {50} \) là:
A. 10
B. 100
C. 20
D. \(\sqrt {52} \)
Câu 3: Điều kiện xác định của phương trình \(\frac{{x - 1}}{{x + 2}} = {\rm{ \;}} - 5\) là:
A. \(x \ne 2\)
B. \(x \ne {\rm{ \;}} - 2\)
C. \(x \ne 1\)
D. \(x \ne 2\) và \(x \ne 1\)
Câu 4: Hình ảnh tổ ong có liên quan đến đa giác đều nào sau đây?

A. Tam giác đều.
B. Tứ giác đều.
C. Ngũ giác đều.
D. Lục giác đều.
Câu 5: Cho tứ giác ABCD nội tiếp một đường tròn.
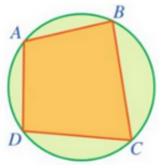
Biết $\angle B = 80^\circ$. Số đo $D$ bằng:
A. $120^\circ$.
B. $110^\circ$.
C. $100^\circ$.
D. $20^\circ$
Câu 6: Cho hàm số \(y = 3{x^2}\). Xác định hệ số \(a\) của \({x^2}\)?
A. \(3\).
B. \( - 3\).
C. \(2\).
D. \(5\).
Câu 7: Trong các số dưới đây, số nào là nghiệm của bất phương trình \(x - 5 > 0\)?
A. \(1\).
B. \(7\).
C. \(0\).
D. \( - 6\).
Câu 8: Một hộp chứa ba viên bi có kích thước đôi một khác nhau. Bạn Nam lấy ngẫu nhiên hai viên bi từ trong hộp. Số phần tử của không gian mẫu của phép thử là:
A. 2.
B. 3.
C. 4.
D. 5.
Câu 9: Gieo một con xúc xắc 30 lần cho kết quả như sau:
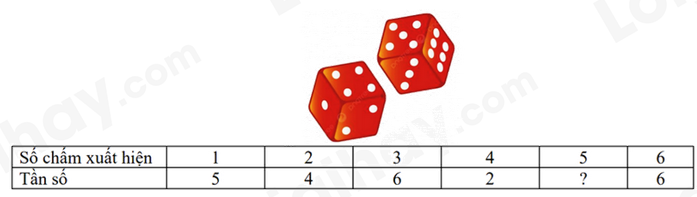
Tần số xuất hiện mặt 5 chấm là
A. 4.
B. 5.
C. 6.
D. 7.
Câu 10: Gieo một con xúc xắc 30 lần cho kết quả như sau:

Tần số tương đối xuất hiện mặt 3 chấm là
A. \(20\% \).
B. \(30\% \).
C. \(16\% \).
D. \(23\% \).
Câu 11: Thể tích của một lon sữa hình trụ có bán kính đáy 6cm và chiều cao 10cm là

A. \(360\pi c{m^3}\).
B. \(600\pi c{m^3}\).
C. \(720\pi c{m^3}\).
D. \(1200\pi c{m^3}\).
Câu 12: Diện tích bề mặt của một quả bóng hình cầu có bán kính 5cm là
A. \(10\pi c{m^2}\)
B. \(400\pi c{m^2}\)
C. \(50\pi c{m^2}\)
D. \(100\pi c{m^2}\)
Phần II. Tự luận
Câu 13:
1) Rút gọn biểu thức \(A = 3\sqrt 2 {\rm{ \;}} + \sqrt {32} \)
2) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 5}\\{4x + y = 9}\end{array}} \right.\)
Câu 14:
1) Giải phương trình \(3{x^2} + 5x - 2 = 0\)
2) Lực \(F\left( N \right)\) của gió tác động lên cánh buồm của con thuyền khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ \(v\left( {m/s} \right)\) của gió theo công thức \(F = a{v^2}\), trong đó \(a\) là một hằng số. Biết rằng khi tốc độ gió là \(2m/s\) thì lực tác động lên cánh buồm của con thuyền bằng 120N. Cánh buồm của thuyền chỉ chịu được lực tác động tối đa là 12000N. Hỏi con thuyền có thể ra khơi khi tốc độ gió là 90km/h hay không?
Câu 15: Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 5dm để làm thành một cái thùng hình hộp chữ nhật không nắp có dung tích 1500 lít. Hãy tính chiều dài và chiều rộng của miếng tôn lúc đầu, biết rằng chiều dài gấp đôi chiều rộng.
Câu 16: Một hộp chứa 60 thẻ cùng loại, trên mỗi thẻ được đánh số từ 1 đến 60. Các thẻ khác nhau ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp đó.
1) Tìm số phần tử của không gian mẫu của phép thử.
2) Tính xác suất của biến cố: “số xuất hiện trên thẻ rút được là số có tổng các chữ số bằng 6”.
Câu 17:
1) Cho nửa đường tròn \(\left( {O;R} \right)\) có đường kính AB. Trên nửa đường tròn lấy điểm \(C\) sao cho \(AC > BC\). Gọi \(H\) là hình chiếu của \(C\) trên AB
a. Chứng minh rằng \(\angle ACO = \angle BCH\)
b. Chứng minh rằng: \(AB.AC = AC.AH + BC.CH\)
2) Một máy bay lên từ mặt đất với vận tốc \(600km/h\). Đường bay lên tạo với phương nằm ngang một góc $23^\circ$. Hỏi sau 1,2 phút máy bay bay lên cao được bao nhiêu kilômét so với mặt đất?
Câu 18:
1) Đà Nẵng có rất nhiều điểm đến độc đáo điển hình như cầu Rồng, cầu quay sông Hàn hay khu du lịch Bà Nà Hills… Bên cạnh đó không thể không kể tới vòng quay mặt trời Sun Wheel – điểm “check-in” quen thuộc của giới trẻ Đà thành. Cho vòng quay mặt trời gồm tám cabin như hình bên. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?
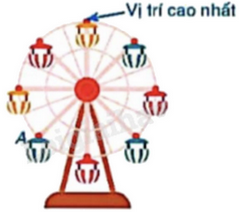
2) Cho 51 số nguyên dương đôi một khác nhau không vượt quá 100. Chứng minh rằng tồn tại hai số trong số 51 số nguyên dương đó có tổng bằng 101.
----- HẾT -----
Lời giải chi tiết
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM
Phần I: Trắc nghiệm

Câu 1 (NB):
Phương pháp:
Căn bậc hai của \(a > 0\) là \(\sqrt a \) và \( - \sqrt a \)
Cách giải:
Căn bậc hai của 16 là \(4\) và \( - 4\)
Chọn D.
Câu 2 (NB):
Phương pháp:
Với a,b không âm ta có \(\sqrt a .\sqrt b {\rm{ \;}} = \sqrt {ab} \)
Cách giải:
Ta có: \(\sqrt 2 .\sqrt {50} {\rm{ \;}} = \sqrt {100} {\rm{ \;}} = 10\)
Chọn A.
Câu 3 (NB):
Phương pháp:
Phân thức \(\frac{{u\left( x \right)}}{{v\left( x \right)}}\) xác định khi \(v\left( x \right) \ne 0\)
Cách giải:
ĐKXĐ: \(x + 2 \ne 0\) hay \(x \ne {\rm{ \;}} - 2\)
Chọn B.
Câu 4 (NB):
Phương pháp:
Quan sát hình ảnh.
Cách giải:
Hình ảnh tổ ong là hình lục giác đều.
Chọn D.
Câu 5 (TH):
Phương pháp:
Tổng 2 góc đối trong tứ giác nội tiếp bằng $180^\circ$
Cách giải:
Tứ giác ABCD nội tiếp đường tròn $\left( O \right)$ nên $\angle B + \angle D = 180^\circ$
Suy ra $80^\circ + \angle D = 180^\circ \Rightarrow \angle D = 100^\circ$
Chọn C.
Câu 6 (NB):
Phương pháp:
Hệ số của \(y = a{x^2}\) là \(a\)
Cách giải:
Hệ số của \({x^2}\) là 3
Chọn A.
Câu 7 (TH):
Phương pháp:
Thay lần lượt từng số vào bất phương trình.
Cách giải:
Thay lần lượt từng số vào bất phương trình ta thấy \(7\) thỏa mãn.
Chọn B.
Câu 8 (TH):
Phương pháp:
Số phần tử của không gian mẫu là tất cả các kết quả có thể xảy ra của phép thử ngẫu nhiên
Cách giải:
Giả sử 3 viên bi là \({a_1},{\mkern 1mu} {\mkern 1mu} {a_2},{\mkern 1mu} {\mkern 1mu} {a_3}\)
Không gian mẫu của phép thử trên là \(\left\{ {\left( {{a_1};{a_2}} \right),{\mkern 1mu} {\mkern 1mu} \left( {{a_2};{a_3}} \right),{\mkern 1mu} {\mkern 1mu} \left( {{a_3};{a_2}} \right)} \right\}\)
Số phần tử của không gian mẫu là 3
Chọn B.
Câu 9 (TH):
Phương pháp:
Tần số xuất hiện mặt 5 chấm bằng tổng số lần giao trừ đi tần số xuất hiện của các mặt còn lại
Cách giải:
Tần số xuất hiện mặt 5 chấm là \(30 - 5 - 4 - 6 - 2 - 6 = 7\)
Chọn D.
Câu 10 (TH):
Phương pháp:
Tần số tương đối \({f_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số \({n_i}\) của giá trị đó và số lượng \(N\) các dữ liệu trong mẫu dữ liệu thống kê: \({f_i} = \frac{{{n_i}}}{N}\)
Cách giải:
Tần số tương đối của mặt 3 chấm là \(\frac{6}{{3 + 4 + 6 + 2 + 7 + 8}} = \frac{1}{5} = 20\% \)
Chọn A.
Câu 11 (TH):
Phương pháp:
Thể tích của khối trụ là \(V = \pi {r^2}h\) với \(r,{\mkern 1mu} {\mkern 1mu} h\) lần lượt là bán kính đáy và chiều cao của khối trụ
Cách giải:
Thể tích của lon sữa là \(V = \pi {r^2}h = \pi {.6^2}.10 = 360\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\)
Chọn A.
Câu 12 (TH):
Phương pháp:
Diện tích bề mặt của hình cầu bán kính \(r\) là \(S = 4\pi {r^2}\)
Cách giải:
Diện tích bề mặt của một quả bóng hình cầu có bán kính 5cm là \(S = 4\pi {r^2} = 4\pi {.5^2} = 100\pi {\mkern 1mu} {\mkern 1mu} (c{m^2})\)
Chọn D.
Phần II. Tự luận
Câu 13 (TH):
Phương pháp:
1) Đưa thừa số ra ngoài dấu căn và rút gọn.
2) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
Cách giải:
1) Ta có: \(A = 3\sqrt 2 {\rm{ \;}} + \sqrt {32} {\rm{ \;}} = 3\sqrt 2 {\rm{ \;}} + 4\sqrt 2 {\rm{ \;}} = 7\sqrt 2 \)
2) \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 5}\\{4x + y = 9}\end{array}} \right.\)
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{3x - y = 5}\\{7x = 14}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{3.2 - y = 5}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.}\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(x = 2,{\mkern 1mu} {\mkern 1mu} y = 1\)
Câu 14 (TH):
Phương pháp:
1) Xét \(\Delta \) và tìm nghiệm của phương trình.
2) Thay số và trả lời bài toán.
Cách giải:
1) \(3{x^2} + 5x - 2 = 0\)
\(\Delta {\rm{ \;}} = {5^2} - 4.3.\left( { - 2} \right) = 49 > 0\)
Phương trình có 2 nghiệm phân biệt \({x_1} = \frac{{ - 5 + 7}}{{2.3}} = \frac{1}{3},{\mkern 1mu} {\mkern 1mu} {x_2} = \frac{{ - 5 - 7}}{{2.3}} = {\rm{ \;}} - 2\)
Vậy phương trình có 2 nghiệm phân biệt \(x = \frac{1}{3},{\mkern 1mu} {\mkern 1mu} x = {\rm{ \;}} - 2\)
2) Thay \(F = 120,{\mkern 1mu} {\mkern 1mu} v = 2\) ta được \(120 = a{.2^2} \Rightarrow a = 30\)
Suy ra \(F = 30{v^2}\)
Với \(F = 12000\) thì \(12000 = 30{v^2} \Rightarrow v = 20\left( {m/s} \right)\)
Tốc độ tối đa có thể di chuyển là \(20m/s\)
Mà \(90km/h = 25m/s\) nên con thuyền không thể ra khơi khi tốc độ gió là 90km/h.
Câu 15 (TH):
Phương pháp:
Gọi chiều rộng của miếng tôn lúc đầu là \(x\) (dm), \(x > 10\)
Từ đó biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Cách giải:
Gọi chiều rộng của miếng tôn lúc đầu là \(x\) (dm), \(x > 10\)
Chiều dài của miếng tôn lúc đầu là \(2x{\mkern 1mu} {\mkern 1mu} \left( {dm} \right)\)
Chiều rộng, chiều dài của cái thùng lần lượt là \(x - 10,{\mkern 1mu} {\mkern 1mu} 2x - 10{\mkern 1mu} {\mkern 1mu} \left( {dm} \right)\)
Vì thể tích thùng là 1500 lít nên ta có phương trình \(5\left( {x - 10} \right)\left( {2x - 10} \right) = 1500\)
\(\begin{array}{*{20}{l}}{\left( {x - 10} \right)\left( {x - 5} \right) = 150}\\{{x^2} - 15x + 50 = 150}\\{{x^2} - 15x - 100 = 0}\\{\left( {x - 20} \right)\left( {x + 5} \right) = 0}\end{array}\)
\(x = 20{\mkern 1mu} {\mkern 1mu} \left( {TM} \right)\); \(x = {\rm{ \;}} - 5{\mkern 1mu} {\mkern 1mu} \left( L \right)\)
Vậy chiều dài, chiều rộng của miếng tôn lúc đầu lần lượt là \(20dm,{\mkern 1mu} {\mkern 1mu} 40dm\)
Câu 16 (TH):
Phương pháp:
Áp dụng công thức tính xác suất = Số kết quả thuận lợi cho biến cố : Số kết quả có thể xảy ra của không gian mẫu.
Cách giải:
1) Số phần tử của không gian mẫu của phép thử là 60
2) Ta có: \(6 = 1 + 5 = 2 + 4 = 3 + 3 = 6 + 0\)
Các kết quả thuận lợi của biến cố “số xuất hiện trên thẻ rút được là số có tổng các chữ số bằng 6” là 15, 51, 24, 42, 33, 6, 60
Có 7 kết quả thuận lợi của biến cố trên
Vậy xác suất của biến cố: “số xuất hiện trên thẻ rút được là số có tổng các chữ số bằng 6” là \(P = \frac{7}{{60}}\)
Câu 17 (VD):
Phương pháp:
1) Vận dụng các tính chất hình học chứng minh.
2) Sử dụng tỉ số lượng giác của góc nhọn.
Cách giải:
1)
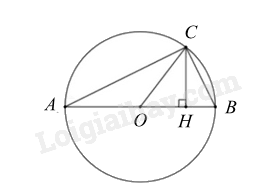
Ta có: $\Delta ACO$ cân tại $O$ (do $OA = OC$)
$\Rightarrow \angle OAC = \angle OCA\,\,\left( 1 \right)$
Vì $C$ thuộc đường tròn đường kính AB nên $\angle ACB = 90^\circ$
Suy ra $\angle ACH + \angle BCH = 90^\circ \,\,\left( 2 \right)$
Lại có: $\angle ACH + \angle CAH = 90^\circ \,\,\left( 3 \right)$ (do $\Delta ACH$ vuông tại $H$)
Từ (1), (2) và (3) suy ra \(\angle ACO = \angle BCH\)
Vậy \(\angle ACO = \angle BCH\)
b) Xét $\Delta ACH$ và $\Delta CBH$ có:
$\begin{array}{l}\angle ACO = \angle BCH\\\angle AHC = \angle BHC = 90^\circ \end{array}$
Suy ra $\Delta ACH\backsim \Delta CBH\left( g.g \right)$
Khi đó \(\frac{{AC}}{{BC}} = \frac{{CH}}{{BH}}\) hay \(AC.BH = BC.CH\)
\(\begin{array}{*{20}{l}}{AC\left( {AB - AH} \right) = BC.CH}\\{AC.AB - AC.AH = BC.CH}\\{AB.AC = AC.AH + BC.CH}\end{array}\)
Vậy \(AB.AC = AC.AH + BC.CH\)
2)
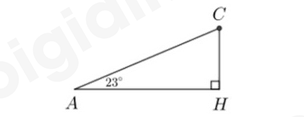
Xét hình vẽ như trên với \(A\) là điểm xuất phát, \(C\) là điểm máy bay tới sau 1,2 phút, \(H\) là hình chiếu vuông góc của \(C\) trên mặt đất
Đổi \(600km/h = 10km/\)phút
Sau 1,2 phút máy bay di chuyển được quãng đường là \(AC = 1,2.10 = 12\left( {km} \right)\)
Áp dụng định lí sin trong tam giác ACH vuông tại \(H\) ta có:
$\sin \angle CAH = \dfrac{{CH}}{{AC}} \Rightarrow CH = AC\sin \angle CAH = 12.\sin 23^\circ \approx 4,7\left( {km} \right)$
Vậy sau 1,2 phút máy bay bay lên cao cách mặt đất 4,7km.
Câu 18 (VDC):
Cách giải:
1) Chia đường tròn thành 8 tám hình quạt bằng nhau (mỗi hình quạt tạo bởi 2 cabin)
Góc tạo bởi 2 cabin là $360^\circ :8 = 45^\circ$
Cabin A cách vị trí cao nhất 3 hình quạt (theo chiều kim đồng hồ)
Như vậy để di chuyển đến vị trí cao nhất thì cabin A cần di chuyển $3.45^\circ = 135^\circ$ quanh tâm
2) Gọi 51 số nguyên dương đã cho lần lượt là \({a_1},{\mkern 1mu} {\mkern 1mu} {a_2}, \ldots ,{\mkern 1mu} {\mkern 1mu} {a_{51}}{\mkern 1mu} {\mkern 1mu} \left( {0 < {a_i} < 101,{\mkern 1mu} {\mkern 1mu} i = \overline {1,51} } \right)\)
Không mất tính tổng quát giả sử \(0 < {a_1} < {a_2} < {\rm{ \;}} \ldots {\rm{ \;}} < {a_{51}} < 101\)
Xét 51 số nguyên dương \(101 - {a_1},{\mkern 1mu} {\mkern 1mu} 101 - {a_2}, \ldots ,101 - {a_{51}}\)
Từ giả thiết trên ta suy ra \(0 < 101 - {a_{51}} < {\rm{ \;}} \ldots {\rm{ \;}} < 101 - {a_2} < 101 - {a_1} < 101\)
Như vậy 102 số nguyên dương trên \({a_1},{\mkern 1mu} {\mkern 1mu} {a_2}, \ldots ,{a_{51}},{\mkern 1mu} {\mkern 1mu} 101 - {a_1},101 - {a_2}, \ldots ,101 - {a_{51}}\) đều nằm trong 100 số nguyên dương \(1,{\mkern 1mu} {\mkern 1mu} 2, \ldots ,100\)
Suy ra trong 102 số đó phải có ít nhất 2 số bằng nhau (2 số thuộc hai nhóm khác nhau)
Gọi 2 số thỏa mãn là \({a_m}\) và \(101 - {a_n}\) (\(1 \le m,n \le 51\))
Rõ ràng \(m \ne n\) vì nếu \(m = n\) thì \({a_m} = 101 - {a_m} \Rightarrow 2{a_m} = 101\) (vô lí)
Như vậy \({a_m} = 101 - {a_n} \Rightarrow {a_m} + {a_n} = 101\) (đpcm)













Danh sách bình luận