Đề thi vào 10 môn Toán Ninh Bình năm 2020
Tải vềCâu 1: 1. Tìm điều kiện của
Đề bài
Câu 1:
1. Tìm điều kiện của \(x\) để biểu thức \(\sqrt {x - 5} \) có nghĩa.
2. Tính \(A = \sqrt {12} + \sqrt {27} - \sqrt {75} \)
3. Rút gọn biểu thức \(P = \left( {\dfrac{1}{{\sqrt a + 2}} + \dfrac{1}{{\sqrt a - 2}}} \right):\dfrac{{\sqrt a }}{{a - 4}}\) với \(a > 0\) và \(a \ne 4\)
Câu 2:
1. Giải hệ phương trình: \(\left\{ \begin{array}{l}x + y = 3\\x - y = 1\end{array} \right.\)
2. Tìm các giá trị của tham số \(m\) để hàm số \(y = mx - 1\) nghịch biến trên \(R\).
3. Xác định tọa độ giao điểm của parabo \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x - 2\)
Câu 3:
Người ta đổ thêm 20 gam nước vào một dung dịch chứa 4 gam muối thì nồng độ của dung dịch giảm đi 10%. Hỏi trước khi đổ thêm nước thì dung dịch chứa bao nhiêu gam nước?
Câu 4:
1. Cho \(\Delta ABC\) nhọn nội tiếp đường tròn tâm \(O\). Hai đường cao BE, CF của \(\Delta ABC\) cắt nhau tại \(H\).
a) Chứng minh tứ giác \(BFEC\) nội tiếp đường tròn.
b) Chứng minh rằng: \(AF.AB = AE.AC\)
c) Kẻ đường kính \(AD\) của đường tròn tâm O. Chứng minh tứ giác BHCD là hình bình hành.
2. Một chiếc máy bay bay lên từ mặt đất với vận tốc \(600\,km/h\). Đường bay lên tạo với phương nằm ngang một góc \({30^0}\). Hỏi sau \(1,5\) phút máy bay bay lên cao được bao nhiêu kilomet theo phương thẳng đứng?
Câu 5:
Cho các số thực dương \(x,y,z\) thỏa mãn \(\sqrt {xy} + \sqrt {yz} + \sqrt {zx} = 2020\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{{x^2}}}{{x + y}} + \dfrac{{{y^2}}}{{y + z}} + \dfrac{{{z^2}}}{{z + x}}\).
Lời giải
Câu 1
Cách giải:
1. Tìm điều kiện của \(x\) để biểu thức \(\sqrt {x - 5} \) có nghĩa.
Biểu thức \(\sqrt {x - 5} \) có nghĩa khi \(x - 5 \ge 0 \Leftrightarrow x \ge 5\)
Vậy với \(x \ge 5\) thì biểu thức \(\sqrt {x - 5} \) có nghĩa.
2. Tính \(A = \sqrt {12} + \sqrt {27} - \sqrt {75} \)
Ta có:
\(\begin{array}{l}A = \sqrt {12} + \sqrt {27} - \sqrt {75} \\ = \sqrt {4.3} + \sqrt {9.3} - \sqrt {25.3} \\ = \sqrt 4 .\sqrt 3 + \sqrt 9 .\sqrt 3 - \sqrt {25} .\sqrt 3 \\ = 2\sqrt 3 + 3\sqrt 3 - 5\sqrt 3 \\ = \sqrt 3 \left( {2 + 3 - 5} \right)\\ = \sqrt 3 .0 = 0\end{array}\)
Vậy \(A = 0.\)
3. Rút gọn biểu thức \(P = \left( {\dfrac{1}{{\sqrt a + 2}} + \dfrac{1}{{\sqrt a - 2}}} \right):\dfrac{{\sqrt a }}{{a - 4}}\) với \(a > 0\) và \(a \ne 4\)
Ta có:
\(\begin{array}{l}P = \left( {\dfrac{1}{{\sqrt a + 2}} + \dfrac{1}{{\sqrt a - 2}}} \right):\dfrac{{\sqrt a }}{{a - 4}}\\ = \left[ {\dfrac{{\sqrt a - 2}}{{\left( {\sqrt a + 2} \right)\left( {\sqrt a - 2} \right)}} + \dfrac{{\sqrt a + 2}}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}} \right].\dfrac{{a - 4}}{{\sqrt a }}\\ = \dfrac{{\sqrt a - 2 + \sqrt a + 2}}{{\left( {\sqrt a + 2} \right)\left( {\sqrt a - 2} \right)}}.\dfrac{{a - 4}}{{\sqrt a }}\\ = \dfrac{{2\sqrt a }}{{a - 4}}.\dfrac{{a - 4}}{{\sqrt a }}\\ = 2\end{array}\)
Vậy \(P = 2\) với \(a > 0\) và \(a \ne 4.\)
Câu 2
Cách giải:
1. Giải hệ phương trình: \(\left\{ \begin{array}{l}x + y = 3\\x - y = 1\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}x + y = 3\\x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 4\\x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2 - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;1} \right)\)
2. Tìm các giá trị của tham số \(m\) để hàm số \(y = mx - 1\) nghịch biến trên \(R\).
Hàm số \(y = mx - 1\) nghịch biến trên \(R\) khi \(m < 0\).
Vậy với \(m < 0\) thì hàm số \(y = mx - 1\) nghịch biến trên \(R\).
3. Xác định tọa độ giao điểm của parabo \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 3x - 2\)
Xét phương trình hoành độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right),\) ta có:
\(\begin{array}{l}{x^2} = 3x - 2\\ \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow {x^2} - 2x - x + 2 = 0\\ \Leftrightarrow x\left( {x - 2} \right) - \left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\end{array}\)
Với \(x = 2 \Rightarrow y = {2^2} = 4\)
Với \(x = 1 \Rightarrow y = {1^2} = 1\)
Vậy tọa độ giao điểm cần tìm là \(\left( {1;1} \right),\left( {2;4} \right)\).
Câu 3
Cách giải:
Người ta đổ thêm 20 gam nước vào một dung dịch chứa 4 gam muối thì nồng độ của dung dịch giảm đi 10%. Hỏi trước khi đổ thêm nước thì dung dịch chứa bao nhiêu gam nước?
Gọi khối lượng nước trước khi đổ thêm là \(x\) (gam) \(\left( {x > 0} \right)\)
Nồng độ dung dịch ban đầu là \(\dfrac{4}{{x + 4}}.100\% \)
Sau khi đổ thêm 20 gam nước thì nồng độ dung dịch là \(\dfrac{4}{{20 + x + 4}}.100\% = \dfrac{4}{{x + 24}}.100\% \)
Vì nồng độ của dung dịch giảm đi 10% nên ta có phương trình:
\(\begin{array}{l}\dfrac{4}{{x + 4}}.100\% - \dfrac{4}{{x + 24}}.100\% = 10\% \\ \Leftrightarrow \dfrac{4}{{x + 4}} - \dfrac{4}{{x + 24}} = \dfrac{1}{{10}}\\ \Leftrightarrow \dfrac{{4x + 96 - 4x - 16}}{{\left( {x + 4} \right)\left( {x + 24} \right)}} = \dfrac{1}{{10}}\\ \Leftrightarrow \dfrac{{80}}{{{x^2} + 28x + 96}} = \dfrac{1}{{10}}\\ \Rightarrow {x^2} + 28x + 96 = 800\\ \Leftrightarrow {x^2} + 28x - 704 = 0\\ \Leftrightarrow {x^2} + 44x - 16x - 704 = 0\\ \Leftrightarrow x\left( {x + 44} \right) - 16\left( {x + 44} \right) = 0\\ \Leftrightarrow \left( {x - 16} \right)\left( {x + 44} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 16 = 0\\x + 44 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\,\left( {tm} \right)\\x = - 44\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy lượng nước ban đầu của dung dịch trước khi đổ thêm là 16 gam.
Câu 4
Cách giải:
1. Cho \(\Delta ABC\) nhọn nội tiếp đường tròn tâm \(O\). Hai đường cao BE, CF của \(\Delta ABC\) cắt nhau tại \(H\).
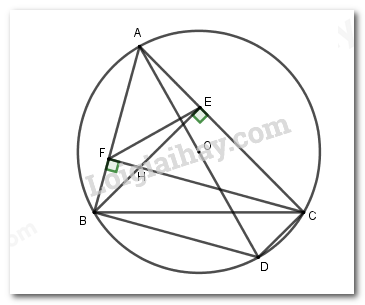
a) Chứng minh tứ giác \(BFEC\) nội tiếp đường tròn.
Ta có:
\(BE\) là đường cao nên \(BE \bot AC \Rightarrow \angle BEC = {90^0}\)
\(CF\) là đường cao nên \(CF \bot AB \Rightarrow \angle BFC = {90^0}\)
Xét tứ giác \(BFEC\) có:
\(\angle BEC = \angle BFC = {90^0}\) nên \(BFEC\) là tứ giác nội tiếp (hai đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau)
Vậy tứ giác \(BFEC\) nội tiếp (đpcm).
b) Chứng minh rằng: \(AF.AB = AE.AC\)
Theo câu a, \(BFEC\) là tứ giác nội tiếp nên \(\angle BFE + \angle BCE = {180^0}\) (tính chất)
Mà \(\angle BFE + \angle AFE = {180^0}\) (kề bù)
Nên \(\angle BCE = \angle BCA = \angle AFE\)
Xét \(\Delta AFE\) và \(\Delta ACB\) có:
\(\angle A\) chung
\(\angle AFE = \angle ACB\left( {cmt} \right)\)
\( \Rightarrow \Delta AFE \sim \Delta ACB\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{AF}}{{AC}} = \dfrac{{AE}}{{AB}}\) (cạnh tương ứng)
\( \Rightarrow AF.AB = AE.AC\) (đpcm)
c) Kẻ đường kính \(AD\) của đường tròn tâm O. Chứng minh tứ giác BHCD là hình bình hành.
\(AD\) là đường kính nên \(\angle ACD = \angle ABD = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow DC \bot AC,DB \bot AB\).
Ta có:
\(\left\{ \begin{array}{l}DC \bot AC\\BH \bot AB\end{array} \right. \Rightarrow DC//BH\) (từ vuông góc đến song song)
\(\left\{ \begin{array}{l}DB \bot AB\\CH \bot AB\end{array} \right. \Rightarrow DB//CH\) (từ vuông góc đến song song)
Tứ giác \(BHCD\) có: \(DC//BH,DB//HC\) nên là hình bình hành. (đpcm)
2. Một chiếc máy bay bay lên từ mặt đất với vận tốc \(600\,km/h\). Đường bay lên tạo với phương nằm ngang một góc \({30^0}\). Hỏi sau \(1,5\) phút máy bay bay lên cao được bao nhiêu kilomet theo phương thẳng đứng?
Đổi \(1,5\) phút \( = \dfrac{{1,5}}{{60}} = \dfrac{1}{{40}}\) giờ
Sau \(\dfrac{1}{{40}}\) giờ máy bay bay được số kilomet theo phương \(AB\) là: \(600.\dfrac{1}{{40}} = 15\left( {km} \right)\)
Sau \(1,5\) phút máy bay bay được số kilomet theo phương thẳng đứng là: \(15.\sin {30^0} = 15.\dfrac{1}{2} = 7,5\left( {km} \right)\).
Vậy sau 1,5 phút, máy bay lên cao được \(7,5km\).
Câu 5
Cách giải:
Cho các số thực dương \(x,y,z\) thỏa mãn \(\sqrt {xy} + \sqrt {yz} + \sqrt {zx} = 2020\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{{x^2}}}{{x + y}} + \dfrac{{{y^2}}}{{y + z}} + \dfrac{{{z^2}}}{{z + x}}\).
Đặt \(\left\{ \begin{array}{l}a = \sqrt x \\b = \sqrt y \\c = \sqrt z \end{array} \right. \Rightarrow a,b,c > 0\)
\(\sqrt {xy} + \sqrt {yz} + \sqrt {zx} = 2020\)\( \Rightarrow ab + bc + ca = 2020\)
Ta có: \(Q = \dfrac{{{a^4}}}{{{a^2} + {b^2}}} + \dfrac{{{b^4}}}{{{b^2} + {c^2}}} + \dfrac{{{c^4}}}{{{c^2} + {a^2}}}\)
Áp dụng BĐT \(\dfrac{{{a^2}}}{x} + \dfrac{{{b^2}}}{y} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{x + y}}\) ta được:
\(\begin{array}{l}Q = \dfrac{{{a^4}}}{{{a^2} + {b^2}}} + \dfrac{{{b^4}}}{{{b^2} + {c^2}}} + \dfrac{{{c^4}}}{{{c^2} + {a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{{a^2} + {b^2} + {b^2} + {c^2}}} + \dfrac{{{c^4}}}{{{c^2} + {a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^2} + {b^2} + {b^2} + {c^2} + {c^2} + {a^2}}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{2\left( {{a^2} + {b^2} + {c^2}} \right)}}\\ = \dfrac{{{a^2} + {b^2} + {c^2}}}{2}\end{array}\)
Lại có:
\(\begin{array}{l}{a^2} + {b^2} \ge 2ab\\{b^2} + {c^2} \ge 2bc\\{c^2} + {a^2} \ge 2ca\\ \Rightarrow 2\left( {{a^2} + {b^2} + {c^2}} \right) \ge 2\left( {ab + bc + ca} \right)\\ \Rightarrow {a^2} + {b^2} + {c^2} \ge ab + bc + ca = 2020\\ \Rightarrow Q \ge \dfrac{{{a^2} + {b^2} + {c^2}}}{2} \ge \dfrac{{2020}}{2} = 1010\\ \Rightarrow Q \ge 1010\end{array}\)
Dấu “=” xảy ra khi \(a = b = c = \sqrt {\dfrac{{2020}}{3}} \Rightarrow x = y = z = \dfrac{{2020}}{3}\)
Vậy GTNN của Q là \(1010\) khi \(x = y = z = \dfrac{{2020}}{3}\)













Danh sách bình luận