Đề thi vào 10 môn Toán Yên Bái năm 2025

Đề bài

PHẦN I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Cho hai số thực \(x\) và \(y\) thỏa mãn \(x > y\). Khẳng định nào sau đây đúng?

A. \(4x < 4y\).

B. \(x - y < 0\).

C. \( - x >  - y\).

D. \(x - 3 > y - 3\).

Câu 2: Hình vẽ sau mô tả đa giác đều nào?

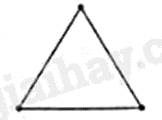
A. Lục giác đều.

B. Tam giác đều.

C. Ngũ giác đều.

D. Hình vuông.

Câu 3: Nghiệm của bất phương trình \(3x + 7 \ge 2\) là:

A. \(x \ge \frac{5}{3}\).

B. \(x \le  - \frac{5}{3}\).

C. \(x \ge  - \frac{5}{3}\).

D. \(x \le \frac{5}{3}\).

Câu 4: Giá trị của biểu thức \(A = \sqrt 7 .\sqrt {28} \) là:

A. 196.

B. 35.

C. 14.

D. 98.

Câu 5: Biểu đồ cột ở hình vẽ sau biểu diễn điểm kiểm tra cuối học kì II môn Toán của học sinh lớp 9A.

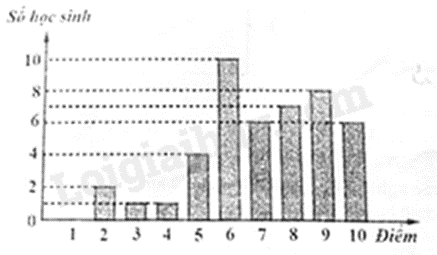
Tần số của điểm 9 là:

A. 6.

B. 8.

C. 9.

D. 7.

Câu 6: Số nào sau đây là ước của 24?

A. 6.

B. 48.

C. 9.

D. 15.

Câu 7: \(\sqrt[3]{{64}}\) bằng:

A. 64.

B. 8.

C. 4.

D. -4.

Câu 8: Hỗn số \(6\frac{2}{3}\) bằng phân số nào sau đây?

A. \(\frac{{20}}{3}\).

B. \(\frac{8}{3}\).

C. \(\frac{{62}}{3}\).

D. \(\frac{{12}}{3}\).

Câu 9: Cho \(x\) và \(y\) là hai số thực khác \(0\) thoả mãn \(5x = 7y\). Tỉ lệ thức nào sau đây đúng?

A. \(\frac{x}{y} = \frac{5}{7}\).

B. \(\frac{x}{5} = \frac{y}{7}\).

C. \(\frac{x}{5} = \frac{7}{y}\).

D. \(\frac{x}{7} = \frac{y}{5}\).

Câu 10: Số đỉnh của một hình hộp chữ nhật là:

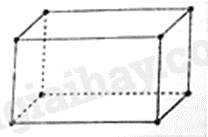
A. 6.

B. 8.

C. 4.

D. 12.

Câu 11: Trong hình vẽ, cho \(DE//BC\), \(AD = 9cm\), \(DB = 15cm\), \(CE = 20cm\). Độ dài của \(AC\) bằng:

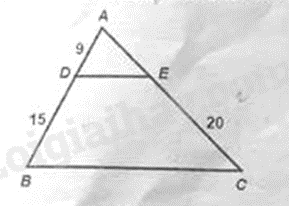
A. \(12cm\).

B. \(\frac{{160}}{3}cm\).

C. \(32cm\).

D. \(\frac{{100}}{3}cm\).

Câu 12: Cho tam giác \(ABC\) vuông tại \(A\). Khẳng định nào sau đây đúng?

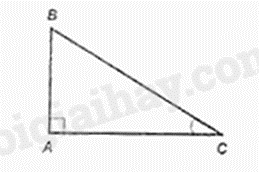
A. \({\rm{tan}}C = \frac{{AC}}{{BC}}\).

B. \({\rm{sin}}C = \frac{{AB}}{{BC}}\).

C. \({\rm{cos}}C = \frac{{BC}}{{AB}}\).

D. \({\rm{cot}}C = \frac{{AB}}{{AC}}\).

PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho đường thẳng \(d:y =  - x + 2\).

a) Hệ số góc của đường thẳng \(d\) là 2.

b) Tung độ giao điểm của đường thẳng \(d\) với trục tung là 2.

c) Đường thẳng \(d\) song song với đường thẳng \(d':y = x + 2\).

d) Biết parabol \(\left( P \right):y = {x^2}\) cắt đường thẳng \(d\) tại hai điểm phân biệt \(A\) và \(B\). Khi đó diện tích của tam giác \(OAB\) bằng 3.

Câu 2: Một hộp có \(15\) chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1,2,3,4,...,15\); hai thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp”.

a) Số phần tử của không gian mẫu là \(15\).

b) Không gian mẫu của phép thử là \({\rm{\Omega }} = \left\{ {1;2;3;4;...;15} \right\}\).

c) Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số nguyên tố” là \(\frac{7}{{15}}\).

d) Xác suất của biến cố “Số xuất hiện trên thẻ là số lẻ và chia cho \(3\) dư \(1\)” là \(\frac{1}{5}\).

Câu 3: Cho đường tròn \((O;3\)cm) và một điểm \(M\) nằm ngoài đường tròn sao cho \(OM = 6\) cm. Từ \(M\) vẽ các tiếp tuyến \(MA\) và \(MB\) của đường tròn \(\left( O \right)\), với \(A,B\) là các tiếp điểm; \(MO\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(C\) và \(D\) (\(C\) thuộc cung nhỏ \(AB\)).

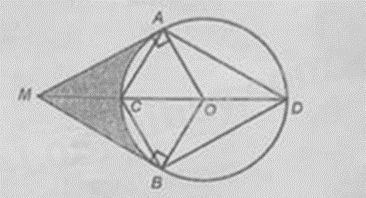
a) Tứ giác \(CADB\) là một tứ giác nội tiếp.

b) \(OB = 3\) cm.

c) \(\widehat {ADB} = {45^ \circ }\).

d) Diện tích của hình giới hạn bởi hai tiếp tuyến \(MA\), \(MB\) và cung nhỏ \(AB\) (phần tô đậm trong hình vẽ) bằng \(3\left( {3\sqrt 3  - \pi } \right)\)cm\(^2\).

Câu 4: Hai lớp \(9A\) và \(9B\) có tổng số \(79\) học sinh. Trong dịp Tết trồng cây năm \(2025\), mỗi học sinh lớp \(9A\) trồng được \(3\) cây và mỗi học sinh lớp \(9B\) trồng được \(2\) cây nên cả hai lớp trồng được tổng số \(200\) cây. Gọi số học sinh của lớp \(9A\) là \(x\) và số học sinh của lớp \(9B\) là \(y\), với \(x,y \in {\mathbb{N}^{\rm{*}}}\).

a) \(x + y = 79\).

b) Tổng số cây trồng được của hai lớp tính theo \(x\) và \(y\) là \(\frac{x}{3} + \frac{y}{2}\).

c) Hệ phương trình mô tả mối liên hệ giữa \(x\) và \(y\) là \(\left\{ {\begin{array}{*{20}{l}}{x + y = 79}\\{3x + 2y = 200}\end{array}} \right.\).

d) Lớp \(9A\) trồng được nhiều hơn \(62\) cây so với lớp \(9B\).

PHẦN III: Câu trắc nghiệm trả lời ngắn. Thi sinh trả lời từ câu 1 đến câu 6.

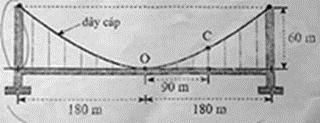
Câu 1: Một cây cầu treo có trụ tháp đôi cao \(60\) m so với mặt cầu và cách nhau \(360\) m. Dây cáp có dạng một đường parabol và được treo trên các đỉnh tháp (hình vẽ). Độ cao của dây cáp tại vị trí \(C\) (cách tâm \(O\) của mặt cầu \(90\) m theo phương ngang) so với mặt cầu là bao nhiêu mét?

Câu 2: Trong một thí nghiệm, một vật rơi tự do từ độ cao 40 m so với mặt đất. Biết quãng đường dịch chuyển được của vật đó tính theo đơn vị mét được cho bởi công thức \(s = 5{t^2}\) với \(t\) là thời gian vật đó rơi, tính theo đơn vị giây (\(t > 0\)). Hỏi sau bao nhiêu giây kể từ lúc rơi thì vật đó chạm đất (làm tròn kết quả đến hàng phần mười)?

Câu 3: Có hai hộp chứa các viên bi với kích thước và khối lượng như nhau. Hộp thứ nhất chứa 1 viên bi xanh và 3 viên bi đỏ. Hộp thứ hai chứa 3 viên bi xanh và 1 viên bi đỏ. Bạn Dương lấy ngẫu nhiên từ mỗi hộp một viên bi. Xác suất của biến cố “Hai viên bi bạn Dương lấy ra cùng màu” là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Câu 4: Biết phương trình \({x^2} + ax + b = 0\) (ẩn \(x\)) có hai nghiệm là 3 và -1. Giá trị của biểu thức \(P = {a^3} + {b^3}\) bằng bao nhiêu?

Câu 5: Một tháp nước được xây dựng trên một con dốc nghiêng \({6^ \circ }\) so với phương ngang. Để tháp đứng thẳng, người ta dùng hai dây cáp cố định tháp như hình vẽ. Biết rằng tháp cao 24m và khoảng cách từ chân tháp đến chỗ cố định dây cáp là 18m. Hỏi dây cáp dài hơn có chiều dài bằng bao nhiêu (làm tròn kết quả đến hàng phần mười của mét)?

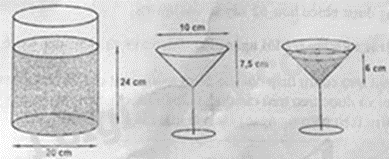
Câu 6: Một bình đựng nước cam có dạng hình trụ với đường kính đáy 20 cm. Phần nước cam trong bình cao 24 cm. Người ta rót nước cam từ bình này vào các ly có hình dạng và kích thước giống nhau. Phần đựng được nước của chiếc ly có dạng hình nón với chiều cao 7,5 cm và đường kính đáy 10 cm. Người ta rót nước cam vào mỗi ly sao cho chiều cao của khối nước cam bằng 6 cm. Hỏi người ta có thể rót được bao nhiêu ly nước cam như vậy? Giả thiết rằng độ dày của bình và ly không đáng kể.

---- HẾT ----

Lời giải chi tiết

PHẦN I: Câu trắc nghiệm nhiều phương án lựa chọn. 

Câu 1: Cho hai số thực \(x\) và \(y\) thỏa mãn \(x > y\). Khẳng định nào sau đây đúng?

A. \(4x < 4y\).

B. \(x - y < 0\).

C. \( - x >  - y\).

D. \(x - 3 > y - 3\).

Phương pháp:

Sử dụng tính chất của bất đẳng thức.

Lời giải:

Với \(x > y\) thì \(4x > 4y\) (nhân cả hai vế với \(4 > 0\)) nên A sai.

Với \(x > y\) thì \(x - y > 0\) nên B sai.

Với \(x > y\) thì \( - x <  - y\) nên C sai.

Với \(x > y\) thì \(x - 3 > y - 3\) (cộng cả hai vế với – 3) nên D đúng.

Đáp án: D

Câu 2: Hình vẽ sau mô tả đa giác đều nào?

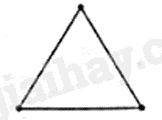
A. Lục giác đều.

B. Tam giác đều.

C. Ngũ giác đều.

D. Hình vuông.

Phương pháp:

Xác định số cạnh của đa giác.

Lời giải:

Vì đa giác đều trên có 3 cạnh nên là tam giác đều.

Đáp án: B

Câu 3: Nghiệm của bất phương trình \(3x + 7 \ge 2\) là:

A. \(x \ge \frac{5}{3}\).

B. \(x \le  - \frac{5}{3}\).

C. \(x \ge  - \frac{5}{3}\).

D. \(x \le \frac{5}{3}\).

Phương pháp:

Giải bất phương trình để tìm nghiệm.

Lời giải:

Ta có:

\(\begin{array}{l}3x + 7 \ge 2\\3x \ge 2 - 7\\3x \ge  - 5\\x \ge  - \frac{5}{3}\end{array}\)

Đáp án: C

Câu 4: Giá trị của biểu thức \(A = \sqrt 7 .\sqrt {28} \) là:

A. 196.

B. 35.

C. 14.

D. 98.

Phương pháp:

Đưa 28 ra ngoài dấu căn rồi tính giá trị của biểu thức.

Lời giải:

\(A = \sqrt 7 .\sqrt {28}  = \sqrt 7 .\sqrt {{2^2}.7}  = \sqrt 7 .2.\sqrt 7  = 2.7 = 14\)

Đáp án: C

Câu 5: Biểu đồ cột ở hình vẽ sau biểu diễn điểm kiểm tra cuối học kì II môn Toán của học sinh lớp 9A.

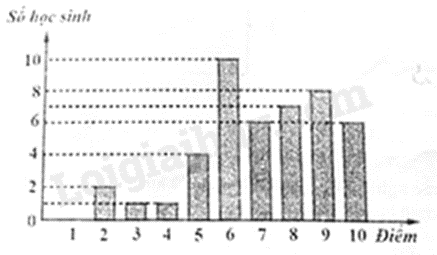
Tần số của điểm 9 là:

A. 6.

B. 8.

C. 9.

D. 7.

Phương pháp:

Xác định giá trị của cột điểm 9.

Lời giải:

Điểm 9 có số học sinh là 8.

Đáp án: B

Câu 6: Số nào sau đây là ước của 24?

A. 6.

B. 48.

C. 9.

D. 15.

Phương pháp:

Để xác định số nào là ước của một số khác, kiểm tra xem số đó có chia hết cho số này không.

Lời giải:

Vì 24 chia hết cho 6 nên 6 là ước của 24.

Đáp án: A

Câu 7: \(\sqrt[3]{{64}}\) bằng:

A. 64.

B. 8.

C. 4.

D. -4.

Phương pháp:

Căn bậc ba của một số a là \(x\) nếu \({x^3} = a\).

Lời giải:

Vì \({4^3} = 64\) nên \(\sqrt[3]{{64}} = 4\).

Đáp án: C

Câu 8: Hỗn số \(6\frac{2}{3}\) bằng phân số nào sau đây?

A. \(\frac{{20}}{3}\).

B. \(\frac{8}{3}\).

C. \(\frac{{62}}{3}\).

D. \(\frac{{12}}{3}\).

Phương pháp:

Đổi hỗn số ra phân số: \(a\frac{b}{c} = \frac{{a.c + b}}{c}\).

Lời giải:

Ta có: \(6\frac{2}{3} = \frac{{6.3 + 2}}{3} = \frac{{20}}{3}\).

Đáp án: A

Câu 9: Cho \(x\) và \(y\) là hai số thực khác \(0\) thoả mãn \(5x = 7y\). Tỉ lệ thức nào sau đây đúng?

A. \(\frac{x}{y} = \frac{5}{7}\).

B. \(\frac{x}{5} = \frac{y}{7}\).

C. \(\frac{x}{5} = \frac{7}{y}\).

D. \(\frac{x}{7} = \frac{y}{5}\).

Phương pháp:

Từ \(ac = bd\) suy ra tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\).

Lời giải:

Vì \(5x = 7y\) nên \(\frac{x}{y} = \frac{7}{5}\) nên A sai.

Vì \(5x = 7y\) nên \(\frac{x}{7} = \frac{y}{5}\) nên D đúng, B, C sai.

Đáp án: D

Câu 10: Số đỉnh của một hình hộp chữ nhật là:

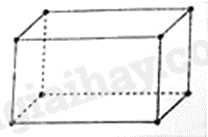
A. 6.

B. 8.

C. 4.

D. 12.

Phương pháp:

Quan sát hình vẽ để xác định.

Lời giải:

Số đỉnh của hình hộp chữ nhật là 8.

Đáp án: B

Câu 11: Trong hình vẽ, cho \(DE//BC\), \(AD = 9cm\), \(DB = 15cm\), \(CE = 20cm\). Độ dài của \(AC\) bằng:

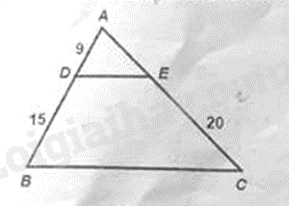
A. \(12cm\).

B. \(\frac{{160}}{3}cm\).

C. \(32cm\).

D. \(\frac{{100}}{3}cm\).

Phương pháp:

Áp dụng định lí Thalès để tính AC.

Lời giải:

Vì DE // BC nên áp dụng định lí Thalès ta có: \(\frac{{BD}}{{AB}} = \frac{{CE}}{{AC}}\) hay \(\frac{{15}}{{9 + 15}} = \frac{{20}}{{AC}}\),

suy ra \(AC = \frac{{20.\left( {9 + 15} \right)}}{{15}} = 32\left( {cm} \right)\)

Đáp án: C

Câu 12: Cho tam giác \(ABC\) vuông tại \(A\). Khẳng định nào sau đây đúng?

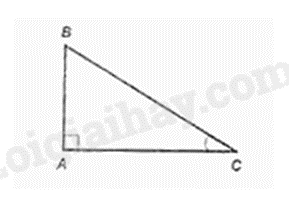
A. \({\rm{tan}}C = \frac{{AC}}{{BC}}\).

B. \({\rm{sin}}C = \frac{{AB}}{{BC}}\).

C. \({\rm{cos}}C = \frac{{BC}}{{AB}}\).

D. \({\rm{cot}}C = \frac{{AB}}{{AC}}\).

Phương pháp:

Áp dụng kiến thức về tỉ số lượng giác.

Lời giải:

Áp dụng tỉ số lượng giác vào tam giác ABC, ta có: \({\rm{sin}}C = \frac{{AB}}{{BC}}\).

Đáp án: B

PHẦN II: Câu trắc nghiệm đúng sai.  

Câu 1: Cho đường thẳng \(d:y =  - x + 2\).

a) Hệ số góc của đường thẳng \(d\) là 2.

b) Tung độ giao điểm của đường thẳng \(d\) với trục tung là 2.

c) Đường thẳng \(d\) song song với đường thẳng \(d':y = x + 2\).

d) Biết parabol \(\left( P \right):y = {x^2}\) cắt đường thẳng \(d\) tại hai điểm phân biệt \(A\) và \(B\). Khi đó diện tích của tam giác \(OAB\) bằng 3.

Phương pháp:

a) Hệ số góc của đường thẳng \(y = ax + b\) là \(a\).

b) Thay \(x = 0\) vào đường thẳng để tính tung độ y tương ứng.

c) Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau nếu \(a = a',b \ne b'\).

d) Xét phương trình hoành độ giao điểm của parabol và đường thẳng để xác định toạ độ điểm A và B.

Dựa vào đồ thị, tính độ dài OB, AB, OA theo định lí Pythagore.

Từ đó chứng minh tam giác OAB vuông tại B, tính diện tích tam giác theo công thức \(S = \frac{1}{2}\). tích hai cạnh góc vuông.

Lời giải:

a) Sai vì hệ số góc của đường thẳng d là a = -1.

b) Đúng vì:

Với \(x = 0\) thì \(y =  - 0 + 2 = 2\) nên giao điểm của đường thẳng d và trục tung có tung độ bằng 2.

c) Sai vì:

Hệ số góc của d là -1; hệ số góc của d’ là 1.

Mà hai đường thẳng song song thì hệ số góc của hai đường thẳng đó bằng nhau nên d không song song với d’.

d) Đúng vì:

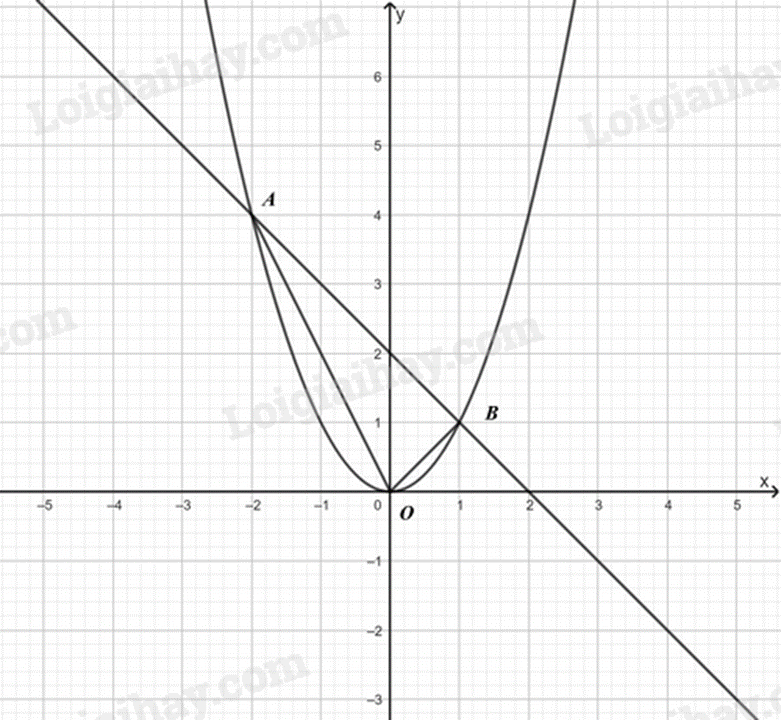
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d là:

\(\begin{array}{l}{x^2} =  - x + 2\\{x^2} + x - 2 = 0\\{x^2} - x + 2x - 2 = 0\\x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\\left( {x + 2} \right)\left( {x - 1} \right) = 0\end{array}\)

nên \({x_A} =  - 2\), \({x_B} = 1\).

Khi đó \({y_A} =  - \left( { - 2} \right) + 2 = 4\), ta được \(A\left( { - 2;4} \right)\).

            \({y_B} =  - 1 + 2 = 1\), ta được \(B\left( {1;1} \right)\).

Dựa vào đồ thị, tính độ dài OB, AB, OA theo định lí Pythagore.

+ Độ dài đoạn OB là: \(\sqrt {{1^2} + {1^2}}  = \sqrt 2 \)

+ Độ dài OA là: \(\sqrt {{2^2} + {4^2}}  = 2\sqrt 5 \)

+ Độ dài đoạn AB là: \(\sqrt {{3^2} + {3^2}}  = 3\sqrt 2 \)

Vì \({\left( {\sqrt 2 } \right)^2} + {\left( {3\sqrt 2 } \right)^2} = {\left( {2\sqrt 5 } \right)^2}\) nên tam giác OAB vuông tại B.

Diện tích tam giác OAB là: \(\frac{1}{2}.\sqrt 2 .3\sqrt 2  = 3\).

Đáp án: SĐSĐ

Câu 2: Một hộp có \(15\) chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1,2,3,4,...,15\); hai thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp”.

a) Số phần tử của không gian mẫu là \(15\).

b) Không gian mẫu của phép thử là \({\rm{\Omega }} = \left\{ {1;2;3;4;...;15} \right\}\).

c) Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số nguyên tố” là \(\frac{7}{{15}}\).

d) Xác suất của biến cố “Số xuất hiện trên thẻ là số lẻ và chia cho \(3\) dư \(1\)” là \(\frac{1}{5}\).

Phương pháp:

a, b) Xác định các kết quả có thể suy ra số phần tử và mô tả không gian mẫu.

c, d) Xác định các kết quả thuận lợi cho biến cố.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi và số phần tử của không gian mẫu.

Lời giải:

a) Đúng vì có 15 thẻ nên số phần tử của không gian mẫu là 15.

b) Đúng vì các kết quả khi rút ngẫu nhiên một thẻ trong hộp là 1; 2; 3; 4;…; 15 nên không gian mẫu của phép thử là \({\rm{\Omega }} = \left\{ {1;2;3;4;...;15} \right\}\).

c) Sai vì:

Các thẻ ghi số nguyên tố là: 2; 3; 5; 7; 11; 13 nên có 5 thẻ ghi số nguyên tố.

Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số nguyên tố” là \(\frac{5}{{15}} = \frac{1}{3}\).

d) Đúng vì:

Các số chia cho 3 dư 1 là: 1; 4; 7; 10; 13.

Các số lẻ trong các số trên là: 1; 7; 13. Có 3 thẻ ghi số lẻ và chia cho 3 dư 1.

Vậy xác suất của biến cố “Số xuất hiện trên thẻ là số lẻ và chia cho \(3\) dư \(1\)” là \(\frac{3}{{15}} = \frac{1}{5}\).

Đáp án: ĐĐSĐ

Câu 3: Cho đường tròn \((O;3\)cm) và một điểm \(M\) nằm ngoài đường tròn sao cho \(OM = 6\) cm. Từ \(M\) vẽ các tiếp tuyến \(MA\) và \(MB\) của đường tròn \(\left( O \right)\), với \(A,B\) là các tiếp điểm; \(MO\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(C\) và \(D\) (\(C\) thuộc cung nhỏ \(AB\)).

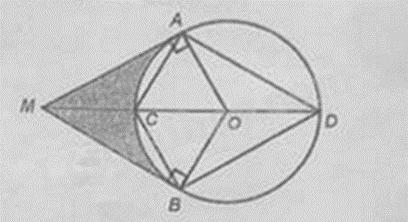
a) Tứ giác \(CADB\) là một tứ giác nội tiếp.

b) \(OB = 3\) cm.

c) \(\widehat {ADB} = {45^ \circ }\).

d) Diện tích của hình giới hạn bởi hai tiếp tuyến \(MA\), \(MB\) và cung nhỏ \(AB\) (phần tô đậm trong hình vẽ) bằng \(3\left( {3\sqrt 3  - \pi } \right)\)cm\(^2\).

Phương pháp:

a) Chứng minh C, A, D, B thuộc đường tròn.

b) OB = bán kính đường tròn ngoại tiếp tứ giác CADB.

c) Chứng minh \(\Delta OAC\) đều suy ra \(\widehat {AOC} = 60^\circ \).

Chứng minh OM là tia phân giác của \(\widehat {AOB}\) nên tính được \(\widehat {AOB}\).

Chứng minh \(\widehat {AOB}\) và \(\widehat {ADB}\) là góc ở tâm và góc nội tiếp cùng chắn cung AB nên tính được \({\kern 1pt} \widehat {ADB}\) dựa vào mối liên hệ giữa góc nội tiếp và góc ở tâm cùng chắn một cung.

d) Áp dụng định lí Pythagore vào tam giác OAM để tính AM, suy ra diện tích tam giác vuông OAM.

Chứng minh \(\Delta OAM = \Delta OBM\) suy ra diện tích tứ giác OAMB.

Tính diện tích hình quạt tròn chắn cung AB nhỏ: \({S_q} = \frac{{\pi {r^2}.n}}{{360}}\) với n là số đo góc ở tâm (số đo cung).

Diện tích hình giới hạn = \({S_{OAMB}} - {S_q}\).

Lời giải:

a) Đúng vì:

Vì C, A, D, B thuộc đường tròn (O; 3cm) nên CADB là tứ giác nội tiếp.

b) Đúng vì:

Vì B thuộc đường tròn (O; 3cm) nên OB = 3cm.

c) Sai vì:

Vì OM = 6cm, OC = 3cm nên MC = 6 – 3 = 3(cm), do đó M là trung điểm của OM.

Vì \(\Delta OAM\) vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên AM = OC.

Mà OC = AO = 3cm nên AM = OC = AO nên \(\Delta OAC\) đều, suy ra \(\widehat {AOC} = 60^\circ \).

Vì MA và MB là tiếp tuyến của (O; 3cm) nên OM là tia phân giác của \(\widehat {AOB}\), suy ra \(\widehat {AOB} = 2\widehat {AOC} = 2.60^\circ  = 120^\circ \).

Mà \(\widehat {AOB}\) và \(\widehat {ADB}\) là góc ở tâm và góc nội tiếp cùng chắn cung AB nên \(\widehat {ADB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.120^\circ  = 60^\circ \).

d) Đúng vì:

Áp dụng định lí Pythagore vào tam giác OAM, ta có:

\(AM = \sqrt {O{M^2} - A{O^2}}  = \sqrt {{6^2} - {3^2}}  = 3\sqrt 3 \).

Suy ra \({S_{\Delta OAM}} = \frac{1}{2}OA.AM = \frac{1}{2}.3.3\sqrt 3  = \frac{{9\sqrt 3 }}{2}\left( {c{m^2}} \right)\)

\(\Delta OAM = \Delta OBM\) (cạnh huyền – cạnh góc vuông) (\(\widehat A = \widehat B = 90^\circ \), OA = OB, OM chung)

nên \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}} = 2.\frac{{9\sqrt 3 }}{2} = 9\sqrt 3 \left( {c{m^2}} \right)\)

Diện tích hình quạt tròn AOB là: \({S_q} = \frac{{\pi {{.3}^2}.120}}{{360}} = 3\pi \)

Suy ra diện tích hình phẳng giới hạn bởi hai tiếp tuyến \(MA\), \(MB\) và cung nhỏ \(AB\) là:

\(9\sqrt 3  - 3\pi  = 3\left( {3\sqrt 3  - \pi } \right)\left( {c{m^2}} \right)\).

Đáp án: ĐĐSĐ

Câu 4: Hai lớp \(9A\) và \(9B\) có tổng số \(79\) học sinh. Trong dịp Tết trồng cây năm \(2025\), mỗi học sinh lớp \(9A\) trồng được \(3\) cây và mỗi học sinh lớp \(9B\) trồng được \(2\) cây nên cả hai lớp trồng được tổng số \(200\) cây. Gọi số học sinh của lớp \(9A\) là \(x\) và số học sinh của lớp \(9B\) là \(y\), với \(x,y \in {\mathbb{N}^{\rm{*}}}\).

a) \(x + y = 79\).

b) Tổng số cây trồng được của hai lớp tính theo \(x\) và \(y\) là \(\frac{x}{3} + \frac{y}{2}\).

c) Hệ phương trình mô tả mối liên hệ giữa \(x\) và \(y\) là \(\left\{ {\begin{array}{*{20}{l}}{x + y = 79}\\{3x + 2y = 200}\end{array}} \right.\).

d) Lớp \(9A\) trồng được nhiều hơn \(62\) cây so với lớp \(9B\).

Phương pháp:

a) Dựa vào tổng số học sinh hai lớp trong đề bài để viết phương trình.

b) Mỗi học sinh lớp 9A trồng được 3 cây thì \(x\) học sinh trồng được \(3x\) cây.

Mỗi học sinh lớp 9B trồng được 2 cây thì \(y\) học sinh trồng được \(2y\) cây.

c) Dựa vào phương trình ý a và lập thêm phương trình tổng số cây để kiểm tra.

d) Tính số học sinh mỗi lớp.

Từ đó tính số cây mỗi lớp trồng được.

Lời giải:

a) Đúng vì:

Hai lớp 9A và 9B có 79 học sinh nên tổng là \(x + y = 79\).

b) Sai vì:

Mỗi học sinh lớp \(9A\) trồng được \(3\) cây và mỗi học sinh lớp \(9B\) trồng được \(2\) cây nên cả hai lớp trồng được: \(3x + 2y\) (cây)

c) Đúng vì:

Phương trình thứ nhất: \(x + y = 79\).

Phương trình thứ hai: \(3x + 2y = 200\) (vì tổng số cây trồng được là 200).

Vậy hệ phương trình mô tả mối liên hệ giữa \(x\) và \(y\) là \(\left\{ {\begin{array}{*{20}{l}}{x + y = 79}\\{3x + 2y = 200}\end{array}} \right.\).

d) Sai vì:

Sử dụng máy tính cầm tay, ta tính được \(\left\{ \begin{array}{l}x = 42\\y = 37\end{array} \right.\)

Suy ra số cây lớp 9A trồng được là: 3.42 = 126 (cây)

Số cây lớp 9B trồng được là: 2.37 = 74 (cây)

Vậy số cây lớp 9A trồng được nhiều hơn lớp 9B là: 126 – 74 = 52 (cây)

Đáp án: ĐSĐS

PHẦN III: Câu trắc nghiệm trả lời ngắn. 

Câu 1: Một cây cầu treo có trụ tháp đôi cao \(60\) m so với mặt cầu và cách nhau \(360\) m. Dây cáp có dạng một đường parabol và được treo trên các đỉnh tháp (hình vẽ). Độ cao của dây cáp tại vị trí \(C\) (cách tâm \(O\) của mặt cầu \(90\) m theo phương ngang) so với mặt cầu là bao nhiêu mét?

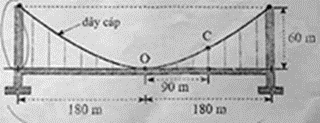
Phương pháp:

Xác định hàm số \(y = a{x^2}\) có đồ thị hàm số là dây cáp.

Thay toạ độ điểm có hoành độ là 180, tung độ là 60 để tính a.

Từ đó thay hoành độ bằng 90 để tính tung độ của điểm C (độ cao của dây cáp tại vị trí C).

Lời giải:

Vì dây cáp có dạng một đường Parabol nên có dạng \(y = a{x^2}\).

Vì đồ thị đi qua điểm (180; 60) nên thay vào \(y = a{x^2}\), ta được: \(a = \frac{y}{{{x^2}}} = \frac{{60}}{{{{180}^2}}} = \frac{1}{{540}}\).

Hàm số là: \(y = \frac{1}{{540}}{x^2}\).

Vì điểm C có hoành độ là 90 nên tung độ của điểm C là: \(y = \frac{1}{{540}}{.90^2} = 15\).

Vậy độ cao của dây cáp tại vị trí \(C\) là 15m.

Đáp án: 15

Câu 2: Trong một thí nghiệm, một vật rơi tự do từ độ cao 40 m so với mặt đất. Biết quãng đường dịch chuyển được của vật đó tính theo đơn vị mét được cho bởi công thức \(s = 5{t^2}\) với \(t\) là thời gian vật đó rơi, tính theo đơn vị giây (\(t > 0\)). Hỏi sau bao nhiêu giây kể từ lúc rơi thì vật đó chạm đất (làm tròn kết quả đến hàng phần mười)?

Phương pháp:

Thời điểm vật chạm đất thì độ cao trở về 0, khi đó tính được quãng đường vật đã di chuyển.

Thay s = quãng đường đã di chuyển để tìm t.

Vì t > 0 nên ta chỉ lấy giá trị t dương.

Lời giải:

Vì vật rơi từ độ cao 40m xuống mặt đất nên quãng đường di chuyển được là 40m.

Khi đó: \(40 = 5{t^2}\), suy ra \({t^2} = \frac{{40}}{5} = 8\)

Do đó \(t = \sqrt 8  \approx 2,8\) (s)

Đáp án: 2,8

Câu 3: Có hai hộp chứa các viên bi với kích thước và khối lượng như nhau. Hộp thứ nhất chứa 1 viên bi xanh và 3 viên bi đỏ. Hộp thứ hai chứa 3 viên bi xanh và 1 viên bi đỏ. Bạn Dương lấy ngẫu nhiên từ mỗi hộp một viên bi. Xác suất của biến cố “Hai viên bi bạn Dương lấy ra cùng màu” là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Phương pháp:

Xác định không gian mẫu, số phần tử của không gian mẫu.

Xác định các kết quả thuận lợi, số kết quả thuận lợi.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi với số phần tử của không gian mẫu.

Lời giải:

Gọi các viên bi của hộp thứ nhất là: X, Đ1, Đ2, Đ3.

Gọi các viên bi của hộp thứ hai là: X1, X2, X3, Đ.

Không gian mẫu của của phép thử là:

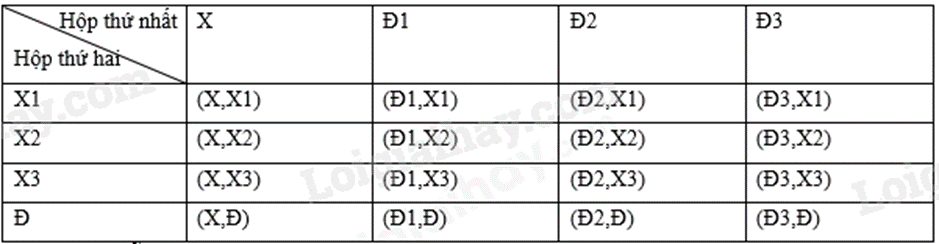
Không gian mẫu của phép thử là 16.

Các kết quả thuận lợi cho biến cố “Hai viên bi bạn Dương lấy ra cùng màu” là:

(X,X1), (X,X2), (X,X3), (Đ1,Đ), (Đ2,Đ), (Đ3,Đ). Có 6 kết quả thuận lợi cho biến cố.

Vậy xác suất của biến cố là: \(\frac{6}{{16}} = 0,375 \approx 0,38\).

Đáp án: 0,38

Câu 4: Biết phương trình \({x^2} + ax + b = 0\) (ẩn \(x\)) có hai nghiệm là 3 và -1. Giá trị của biểu thức \(P = {a^3} + {b^3}\) bằng bao nhiêu?

Phương pháp:

Thay hai nghiệm vào phương trình, đưa về hệ hai phương trình bậc nhất ẩn a, b để tính a, b.

Thay a, b tìm được vào P để tính giá trị.

Lời giải:

Vì phương trình có hai nghiệm là 3 và – 1 nên ta có:

\(\left\{ \begin{array}{l}{3^2} + a.3 + b = 0\\{\left( { - 1} \right)^2} + a.\left( { - 1} \right) + b = 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}3a + b =  - 9\\ - a + b =  - 1\end{array} \right.\)

Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}a =  - 2\\b =  - 3\end{array} \right.\).

Suy ra \(P = {\left( { - 2} \right)^3} + {\left( { - 3} \right)^3} =  - 35\).

Đáp án: -35

Câu 5: Một tháp nước được xây dựng trên một con dốc nghiêng \({6^ \circ }\) so với phương ngang. Để tháp đứng thẳng, người ta dùng hai dây cáp cố định tháp như hình vẽ. Biết rằng tháp cao 24m và khoảng cách từ chân tháp đến chỗ cố định dây cáp là 18m. Hỏi dây cáp dài hơn có chiều dài bằng bao nhiêu (làm tròn kết quả đến hàng phần mười của mét)?

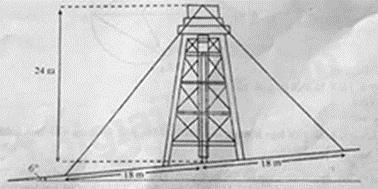
Phương pháp:

Hạ đường vuông góc từ đỉnh xuống mặt đất.

Xác định góc tạo bởi chân đáy với mặt đất.

Sử dụng hệ thức lượng trong tam giác để tính khoảng cách từ đỉnh xuống mặt đất và khoảng cách giữa chân đáy với đường cao.

Áp dụng định lí Pythagore để tính chiều dài của dây cáp dài hơn.

Lời giải:

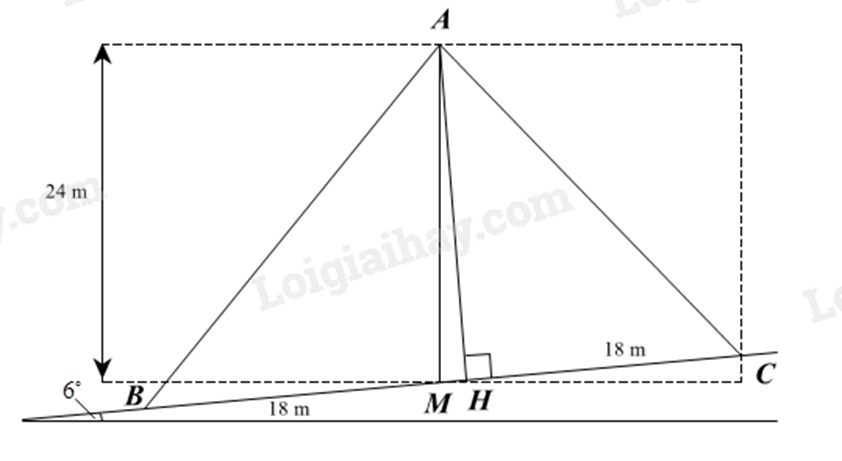
Gọi các điểm như hình vẽ. Khi đó ta có: AM = 24 m, BM = MC = 18 m.

Hạ đường vuông góc AH kẻ từ A xuống BC (H \( \in \) BC).

Vì con dốc nghiêng \(6^\circ \) nên góc tạo bởi CM và mặt đất là \(6^\circ \), suy ra \(\widehat {AMH} = 90^\circ  - 6^\circ  = 84^\circ \).

Áp dụng hệ thức lượng trong tam giác, ta có:

AH = \(AM.\sin \widehat {AMH} = 24.\sin 84^\circ \),

MH = \(AM.\cos \widehat {AMH} = 24.\cos 84^\circ \).

Suy ra độ dài BH là: \(BH = BM + MH = 18 + 24.\cos 84^\circ \).

Áp dụng định lí Pythagore vào tam giác ABH, ta có:

\(\begin{array}{l}AB = \sqrt {A{H^2} + B{H^2}} \\ = \sqrt {{{\left( {24.\sin 84^\circ } \right)}^2} + {{\left( {18 + 24.\cos 84^\circ } \right)}^2}}  \approx 31,5\left( m \right)\end{array}\)

Vậy dây cáp dài hơn có chiều dài khoảng 31,5 m.

Đáp án: 31,5

Câu 6: Một bình đựng nước cam có dạng hình trụ với đường kính đáy 20 cm. Phần nước cam trong bình cao 24 cm. Người ta rót nước cam từ bình này vào các ly có hình dạng và kích thước giống nhau. Phần đựng được nước của chiếc ly có dạng hình nón với chiều cao 7,5 cm và đường kính đáy 10 cm. Người ta rót nước cam vào mỗi ly sao cho chiều cao của khối nước cam bằng 6 cm. Hỏi người ta có thể rót được bao nhiêu ly nước cam như vậy? Giả thiết rằng độ dày của bình và ly không đáng kể.

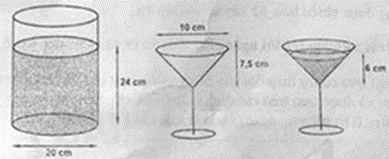
Phương pháp:

Tính thể tích phần nước cam trong bình theo công thức tính thể tích hình trụ: \({V_t} = \pi {r^2}h\).

Áp dụng định lí hai tam giác bằng nhau (hoặc hệ quả của định lí Thalès) để tính bán kính đáy phần nước cam trong ly theo bán kính đáy của ly.

Tính thể tích nước cam theo công thức tính thể tích hình nón: \({V_n} = \frac{1}{3}\pi {r^2}h\).

Lời giải:

Thể tích phần nước cam trong bình là: \({V_t} = \pi .{\left( {\frac{{20}}{2}} \right)^2}.24 = 2400\pi \left( {c{m^3}} \right)\).

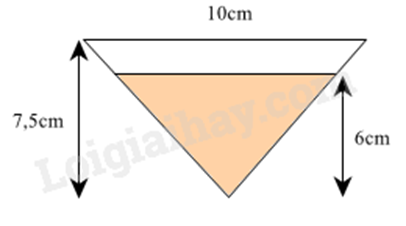
Vì mặt cắt của hình nón là tam giác và đường kính đáy phần nước cam và đáy ly là hai đường thẳng song song nên tạo thành hai tam giác đồng dạng nên đường kính đáy phần nước cam : đường kính đáy ly = chiều cao phần nước cam : chiều cao ly.

Do đó: \(\frac{{{d_{nc}}}}{{10}} = \frac{6}{{7,5}}\) nên đường kính phần nước cam là: \(\frac{{6.10}}{{7,5}} = 8\left( {cm} \right)\), suy ra bán kính phần nước cam là: \(\frac{8}{2} = 4\left( {cm} \right)\).

Thể tích phần nước cam của mỗi ly là: \(\frac{1}{3}\pi {.4^2}.6 = 32\pi \left( {c{m^3}} \right)\)

Vậy người ta có thể rót được số ly nước cam là: \(\frac{{2400\pi }}{{32\pi }} = 75\) (ly)

Đáp án: 75