Đề thi học kì 2 Toán 12 Cánh diều - Đề số 5
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Biết \(\int\limits_1^5 {\frac{{dx}}{x}} = \ln a\) với \(a \in \mathbb{Q}\). Giá trị của a là
-
A.
125
-
B.
25
-
C.
1
-
D.
5
Cho \(F\left( x \right) = {x^3}\) là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\). Giá trị của \(\int\limits_0^2 {\left[ { - 4 + f(x)} \right]dx} \) bằng
-
A.
0
-
B.
-4
-
C.
12
-
D.
2
Họ tất cả các nguyên hàm của hàm số \(y = {3^{2x + 1}}\) là
-
A.
\(\frac{{{3^{2x + 1}}}}{{2\ln 3}} + C\)
-
B.
\({3^{2x + 1}}.\ln 3 + C\)
-
C.
\(\frac{{{3^{2x + 1}}.\ln 3}}{2} + C\)
-
D.
\({3^{2x + 1}} + C\)
Diện tích S của hình phẳng giới hạn bởi các đường \(y = 2{x^2}\), y = -1, x = 0, x = 1 được tính bởi công thức nào sau đây?
-
A.
\(S = \pi \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \)
-
B.
\(S = \int\limits_0^1 {\left( {2{x^2} - 1} \right)dx} \)
-
C.
\(S = \int\limits_0^1 {{{\left( {2{x^2} + 1} \right)}^2}dx} \)
-
D.
\(S = \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \)
Trong không gian Oxyz, cho đường thẳng \(\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\). Vecto nào dưới đây là một vecto chỉ phương của d?
-
A.
\(\overrightarrow {{u_1}} = (2;1; - 3)\)
-
B.
\(\overrightarrow {{u_2}} = ( - 2; - 1;3)\)
-
C.
\(\overrightarrow {{u_3}} = ( - 1;2;1)\)
-
D.
\(\overrightarrow {{u_4}} = ( - 1;2; - 1)\)
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm A(1;2;-3) và có vecto pháp tuyến \(\overrightarrow n = (1; - 2;3)\)?
-
A.
x – 2y + 3z – 12 = 0
-
B.
x – 2y – 3z + 6 = 0
-
C.
x – 2y + 3z + 12 = 0
-
D.
x – 2y – 3z – 6 = 0
Trong không gian Oxy, cho điểm M(1;2;3) và đường thẳng \(\Delta \): \(\frac{{x - 2}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{1}\). Mặt phẳng đi qua M và vuông góc với \(\Delta \) có phương trình là
-
A.
2x – 2y + 3z – 7 = 0
-
B.
x + 2y + 3z – 3 = 0
-
C.
2x – y + z + 3 = 0
-
D.
2x – y + z – 3 = 0
Phương trình nào dưới đây là phương trình chính tắc của đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3t\\z = - 2 + t\end{array} \right.\)?
-
A.
\(\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 2}}{1}\)
-
B.
\(\frac{{x - 1}}{2} = \frac{y}{3} = \frac{{z + 2}}{1}\)
-
C.
\(\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 2}}{{ - 2}}\)
-
D.
\(\frac{{x - 1}}{1} = \frac{y}{3} = \frac{{z + 2}}{{ - 2}}\)
Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt cầu có tâm I(7;6;-5) và bán kính 9?
-
A.
\({\left( {x + 7} \right)^2} + {\left( {y + 6} \right)^2} + {\left( {z - 5} \right)^2} = 81\)
-
B.
\({\left( {x + 7} \right)^2} + {\left( {y + 6} \right)^2} + {\left( {z - 5} \right)^2} = 9\)
-
C.
\({\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 5} \right)^2} = 81\)
-
D.
\({\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 5} \right)^2} = 9\)
Trong không gian Oxyz, viết phương trình mặt cầu có tâm I(0;1;3) và tiếp xúc với mặt phẳng (P): x + 2y – z + 3 = 0.
-
A.
\({x^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = \frac{2}{3}\)
-
B.
\({x^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = \frac{1}{6}\)
-
C.
\({x^2} + {\left( {y - 1} \right)^2} + {\left( {z + 3} \right)^2} = \frac{2}{3}\)
-
D.
\({x^2} + {\left( {y + 1} \right)^2} + {\left( {z + 3} \right)^2} = \frac{1}{6}\)
Cho \(P(A) = \frac{2}{5}\), \(P(B|\overline A ) = \frac{1}{4}\). Giá trị của \(P(B\overline A )\) là
-
A.
\(\frac{1}{7}\)
-
B.
\(\frac{4}{{19}}\)
-
C.
\(\frac{4}{{21}}\)
-
D.
\(\frac{3}{{20}}\)
Cho hai biến cố A và B. Biết rằng P(B) = 0,4, P(A|B) = 0,8, \(P(A|\overline B ) = 0,5\). Tính P(A).
-
A.
0,4
-
B.
0,65
-
C.
0,62
-
D.
0,48
a) Hình phẳng (H) được giới hạn bởi đồ thị hàm số \(y = f(x) = \frac{1}{2}x + 1\), Ox, Oy, x = 2.
b) Thể tích V của khối tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox được tính bằng công thức \(V = \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} \).
c) Hình phẳng (H) có diện tích bằng 4 (đvdt).
d) Thể tích V của khối tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox bằng \(\frac{{14\pi }}{3}\) (đvdt).
Trong không gian với hệ tọa độ Oxyz, tâm I(-2;1;5), bán kính bằng 3. Cho các điểm A(10;1;2), B(0;1;4), C(0;3;4).
a) Phương trình mặt cầu (S) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 5} \right)^2} = 3\).
b) Điểm A ngoài mặt cầu (S).
c) Đường thẳng AB cắt mặt cầu (S).
d) Mặt phẳng (ABC) cắt (S) theo giao tuyến là đường tròn có bán kính bằng 3.
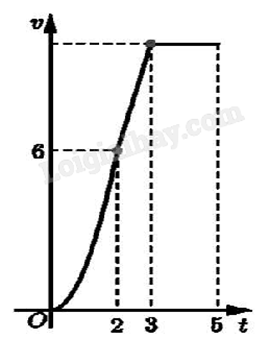
Một chiếc xe đua F1 đạt tới vận tốc lớn nhất là 360 km/h. Đồ thị bên biểu thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol đỉnh tại gốc tọa độ O, giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trục tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu mét?
Trong không gian Oxyz, cho điểm A(1;-1;2), mặt phẳng (P): x + y – 2z + 5 = 0 và đường thẳng d: \(\frac{{x + 1}}{2} = \frac{y}{1} = \frac{{z - 2}}{1}\). Đường thẳng \(\Delta \) cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Phương trình đường thẳng \(\Delta \) có dạng \(\frac{{x + 9}}{a} = \frac{{y - {y_0}}}{3} = \frac{{z - {z_0}}}{b}\) với \(ab \ne 0\). Tính \({a^2} + {b^2} + {y_0}^2 + {z_0}^2\).
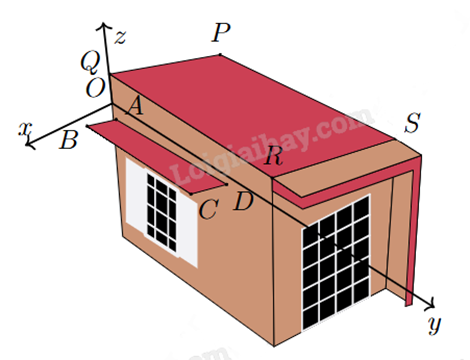
Hình bên vẽ minh họa mái hiên ABCD song song với mái nhà PQRS trong không gian với hệ tọa độ Oxyz (mái hiên và mái nhà đều phẳng) có Q(-10; 0; 200), P(-490; 0; 200), R(0; 1600; 0) và A(0; 0; -65). Mặt phẳng (ABCD) có phương trình y + az + 65a = 0. Tìm giá trị của a.
Trong một khoa cấp cứu của bệnh viện, người ta thống kê rằng 60% bệnh nhân bị chấn thương đầu là do tai nạn giao thông và còn lại là do tai nạn khác. Loại chấn thương đầu do tai nạn giao thông gây tử vong bệnh nhân chiếm 50% và loại chấn thương do tai nạn khác gây tử vong ở bệnh nhân chiếm 30%. Xác suất một bệnh án của bệnh nhân tử vong ở khoa cấp cứu đó bằng bao nhiêu?
Lời giải và đáp án
Biết \(\int\limits_1^5 {\frac{{dx}}{x}} = \ln a\) với \(a \in \mathbb{Q}\). Giá trị của a là
-
A.
125
-
B.
25
-
C.
1
-
D.
5
Đáp án : D
Áp dụng công thức \(\int {\frac{{dx}}{x}} = \ln \left| x \right| + C\) và định nghĩa tích phân.
\(\int\limits_1^5 {\frac{{dx}}{x}} = \ln \left| x \right|\left| {\begin{array}{*{20}{c}}{^5}\\{_1}\end{array}} \right. = \ln 5 - \ln 1 = \ln 5\).
Cho \(F\left( x \right) = {x^3}\) là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\). Giá trị của \(\int\limits_0^2 {\left[ { - 4 + f(x)} \right]dx} \) bằng
-
A.
0
-
B.
-4
-
C.
12
-
D.
2
Đáp án : B
Áp dụng tính chất của tích phân.
\(\int\limits_0^2 {\left[ { - 4 + f(x)} \right]dx} = - \int\limits_0^2 {4dx} + \int\limits_0^2 {{x^3}dx} = - 8 + 4 = - 4\).
Họ tất cả các nguyên hàm của hàm số \(y = {3^{2x + 1}}\) là
-
A.
\(\frac{{{3^{2x + 1}}}}{{2\ln 3}} + C\)
-
B.
\({3^{2x + 1}}.\ln 3 + C\)
-
C.
\(\frac{{{3^{2x + 1}}.\ln 3}}{2} + C\)
-
D.
\({3^{2x + 1}} + C\)
Đáp án : A
Đưa \(y = {3^{2x + 1}}\) về dạng \(y = {a^x}\) rồi áp dụng công thức nguyên hàm \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\).
\(\int {{3^{2x + 1}}dx} = \int {{{\left( {{3^2}} \right)}^x}.3dx} = 3\int {{9^x}dx} = 3.\frac{{{9^x}}}{{\ln 9}} + C = \frac{{{{\left( {{3^2}} \right)}^x}.3}}{{\ln {3^2}}} + C = \frac{{{3^{2x + 1}}}}{{2\ln 3}} + C\).
Diện tích S của hình phẳng giới hạn bởi các đường \(y = 2{x^2}\), y = -1, x = 0, x = 1 được tính bởi công thức nào sau đây?
-
A.
\(S = \pi \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \)
-
B.
\(S = \int\limits_0^1 {\left( {2{x^2} - 1} \right)dx} \)
-
C.
\(S = \int\limits_0^1 {{{\left( {2{x^2} + 1} \right)}^2}dx} \)
-
D.
\(S = \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \)
Đáp án : D
Áp dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x), hai đường thẳng x = a, x = b: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \).
Ta có \(2{x^2} + 1 > 0\) với mọi x, suy ra \(\left| {2{x^2} + 1} \right| = 2{x^2} + 1\).
\(S = \int\limits_0^1 {\left| {2{x^2} - ( - 1)} \right|dx} = \int\limits_0^1 {\left| {2{x^2} + 1} \right|dx} = \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \).
Trong không gian Oxyz, cho đường thẳng \(\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\). Vecto nào dưới đây là một vecto chỉ phương của d?
-
A.
\(\overrightarrow {{u_1}} = (2;1; - 3)\)
-
B.
\(\overrightarrow {{u_2}} = ( - 2; - 1;3)\)
-
C.
\(\overrightarrow {{u_3}} = ( - 1;2;1)\)
-
D.
\(\overrightarrow {{u_4}} = ( - 1;2; - 1)\)
Đáp án : C
Đường thẳng \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) có một vecto chỉ phương là \(\overrightarrow u = (a;b;c)\).
Đường thẳng \(\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\) có một vecto chỉ phương là \(\overrightarrow {{u_3}} = ( - 1;2; 1)\).
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm A(1;2;-3) và có vecto pháp tuyến \(\overrightarrow n = (1; - 2;3)\)?
-
A.
x – 2y + 3z – 12 = 0
-
B.
x – 2y – 3z + 6 = 0
-
C.
x – 2y + 3z + 12 = 0
-
D.
x – 2y – 3z – 6 = 0
Đáp án : C
Mặt phẳng đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\), nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình tổng quát là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Mặt phẳng đi qua điểm A(1;2;-3) và có vecto pháp tuyến \(\overrightarrow n = (1; - 2;3)\) có phương trình là \(1\left( {x - 1} \right) - 2\left( {y - 2} \right) + 3\left( {z + 3} \right) = 0 \Leftrightarrow x - 2y + 3z + 12 = 0\).
Trong không gian Oxy, cho điểm M(1;2;3) và đường thẳng \(\Delta \): \(\frac{{x - 2}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{1}\). Mặt phẳng đi qua M và vuông góc với \(\Delta \) có phương trình là
-
A.
2x – 2y + 3z – 7 = 0
-
B.
x + 2y + 3z – 3 = 0
-
C.
2x – y + z + 3 = 0
-
D.
2x – y + z – 3 = 0
Đáp án : D
Mặt phẳng cần tìm đi qua M, nhận vecto chỉ phương của \(\Delta \) làm vecto pháp tuyến.
Vecto chỉ phương của \(\Delta \) là \(\overrightarrow u = (2; - 1;1)\), đồng thời cũng là vecto pháp tuyến của mặt phẳng cần tìm.
Phương trình mặt phẳng đi qua M, nhận \(\overrightarrow u \) làm vecto pháp tuyến là:
\(2(x - 1) - 1(y - 2) + 1(z - 3) = 0 \Leftrightarrow 2x - y + z - 3 = 0\).
Phương trình nào dưới đây là phương trình chính tắc của đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3t\\z = - 2 + t\end{array} \right.\)?
-
A.
\(\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 2}}{1}\)
-
B.
\(\frac{{x - 1}}{2} = \frac{y}{3} = \frac{{z + 2}}{1}\)
-
C.
\(\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 2}}{{ - 2}}\)
-
D.
\(\frac{{x - 1}}{1} = \frac{y}{3} = \frac{{z + 2}}{{ - 2}}\)
Đáp án : B
Biểu diễn t theo x, y, z rồi viết phương trình chính tắc.
Ta có \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3t\\z = - 2 + t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = \frac{{x - 1}}{2}\\t = \frac{y}{3}\\t = z + 2\end{array} \right. \Rightarrow t = \frac{{x - 1}}{2} = \frac{y}{3} = \frac{{z + 2}}{1}\).
Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt cầu có tâm I(7;6;-5) và bán kính 9?
-
A.
\({\left( {x + 7} \right)^2} + {\left( {y + 6} \right)^2} + {\left( {z - 5} \right)^2} = 81\)
-
B.
\({\left( {x + 7} \right)^2} + {\left( {y + 6} \right)^2} + {\left( {z - 5} \right)^2} = 9\)
-
C.
\({\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 5} \right)^2} = 81\)
-
D.
\({\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 5} \right)^2} = 9\)
Đáp án : C
Mặt cầu tâm I(a;b;c), bán kính R có phương trình là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Phương trình của mặt cầu tâm I(7;6;-5), bán kính bằng 9 là \({\left( {x - 7} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 5} \right)^2} = 81\).
Trong không gian Oxyz, viết phương trình mặt cầu có tâm I(0;1;3) và tiếp xúc với mặt phẳng (P): x + 2y – z + 3 = 0.
-
A.
\({x^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = \frac{2}{3}\)
-
B.
\({x^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = \frac{1}{6}\)
-
C.
\({x^2} + {\left( {y - 1} \right)^2} + {\left( {z + 3} \right)^2} = \frac{2}{3}\)
-
D.
\({x^2} + {\left( {y + 1} \right)^2} + {\left( {z + 3} \right)^2} = \frac{1}{6}\)
Đáp án : A
Lập phương trình mặt cầu tâm I, bán kính \(R = d\left( {I,(P)} \right)\).
Bán kính mặt cầu là khoảng cách từ tâm I đến mặt phẳng (P).
\(R = d\left( {I,(P)} \right) = \frac{{\left| {1.0 + 2.1 - 1.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2} + {{( - 1)}^2}} }} = \frac{2}{{\sqrt 6 }} = \sqrt {\frac{2}{3}} \).
Phương trình mặt cầu tâm I(0;1;3), bán kính \(R = \sqrt {\frac{2}{3}} \) là \({x^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = \frac{2}{3}\).
Cho \(P(A) = \frac{2}{5}\), \(P(B|\overline A ) = \frac{1}{4}\). Giá trị của \(P(B\overline A )\) là
-
A.
\(\frac{1}{7}\)
-
B.
\(\frac{4}{{19}}\)
-
C.
\(\frac{4}{{21}}\)
-
D.
\(\frac{3}{{20}}\)
Đáp án : D
Áp dụng công thức nhân xác suất: P(AB) = P(A).P(B|A).
Ta có \(P(\overline A ) = 1 - P(A) = 1 - \frac{2}{5} = \frac{3}{5}\).
Áp dụng công thức nhân xác suất: \(P(B\overline A ) = P(\overline A ).P(B|\overline A ) = \frac{3}{5}.\frac{1}{4} = \frac{3}{{20}}\).
Cho hai biến cố A và B. Biết rằng P(B) = 0,4, P(A|B) = 0,8, \(P(A|\overline B ) = 0,5\). Tính P(A).
-
A.
0,4
-
B.
0,65
-
C.
0,62
-
D.
0,48
Đáp án : C
Áp dụng công thức tính xác suất toàn phần.
\(P(\overline B ) = 1 - P(B) = 1 - 0,4 = 0,6\).
\(P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B ) = 0,4.0,8 + 0,6.0,5 = 0,62\).
a) Hình phẳng (H) được giới hạn bởi đồ thị hàm số \(y = f(x) = \frac{1}{2}x + 1\), Ox, Oy, x = 2.
b) Thể tích V của khối tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox được tính bằng công thức \(V = \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} \).
c) Hình phẳng (H) có diện tích bằng 4 (đvdt).
d) Thể tích V của khối tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox bằng \(\frac{{14\pi }}{3}\) (đvdt).
a) Hình phẳng (H) được giới hạn bởi đồ thị hàm số \(y = f(x) = \frac{1}{2}x + 1\), Ox, Oy, x = 2.
b) Thể tích V của khối tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox được tính bằng công thức \(V = \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} \).
c) Hình phẳng (H) có diện tích bằng 4 (đvdt).
d) Thể tích V của khối tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox bằng \(\frac{{14\pi }}{3}\) (đvdt).
Áp dụng tích phân tính diện tích hình phẳng, thể tích khối tròn xoay.
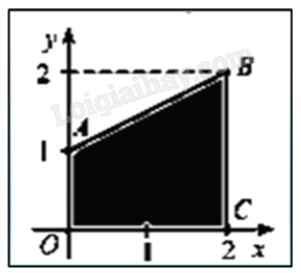
a) Đúng. Đường thẳng AB có dạng y = ax + b (a > 0), đi qua A(0;1) và B(2;2).
Ta có \(\left\{ \begin{array}{l}1 = a.0 + b\\2 = a.2 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = 1\end{array} \right. \Rightarrow y = \frac{1}{2}x + 1\).
Vậy hình phẳng (H) được giới hạn bởi đồ thị hàm số \(y = \frac{1}{2}x + 1\), Ox, Oy, x = 2.
b) Sai. Thể tích khối tròn xoay sinh ra khi quay (H) quanh Ox là \(V = \pi \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} \).
c) Sai. Diện tích hình phẳng (H) là \(V = \int\limits_0^2 {\left| {\frac{1}{2}x + 1} \right|dx} = \int\limits_0^2 {\left( {\frac{1}{2}x + 1} \right)dx} = 3\) (đvdt).
d) Đúng. Thể tích khối tròn xoay sinh ra khi quay (H) quanh Ox là \(V = \pi \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} = \frac{{14\pi }}{3}\) (đvdt).
Trong không gian với hệ tọa độ Oxyz, tâm I(-2;1;5), bán kính bằng 3. Cho các điểm A(10;1;2), B(0;1;4), C(0;3;4).
a) Phương trình mặt cầu (S) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 5} \right)^2} = 3\).
b) Điểm A ngoài mặt cầu (S).
c) Đường thẳng AB cắt mặt cầu (S).
d) Mặt phẳng (ABC) cắt (S) theo giao tuyến là đường tròn có bán kính bằng 3.
a) Phương trình mặt cầu (S) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 5} \right)^2} = 3\).
b) Điểm A ngoài mặt cầu (S).
c) Đường thẳng AB cắt mặt cầu (S).
d) Mặt phẳng (ABC) cắt (S) theo giao tuyến là đường tròn có bán kính bằng 3.
a) Lập phương trình mặt cầu (S) tâm I(-2;1;5), bán kính bằng 3.
b) Tính IA và so sánh với bán kính mặt cầu.
c) Tính IB, nhận xét vị trí của A, B so với mặt cầu rồi kết luận.
d) Vậy (S) cắt mặt phẳng (ABC) theo giao tuyến là đường tròn có bán kính \(\sqrt {{R^2} - {d^2}\left( {I,(ABC)} \right)} \).
a) Sai. Phương trình mặt cầu (S) tâm I(-2;1;5), bán kính bằng 3 là:
\({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 5} \right)^2} = {3^2} \Leftrightarrow {\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 5} \right)^2} = 9\).
b) Đúng. \(IA = \sqrt {{{\left( {10 + 2} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}} = 3\sqrt {17} > 3\) nên điểm A nằm ngoài mặt cầu.
c) Đúng. \(IB = \sqrt {{{\left( {0 + 2} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 5 < 3\) nên điểm B nằm trong mặt cầu.
Vì A nằm ngoài mặt cầu, B nằm trong mặt cầu nên đường thẳng AB cắt mặt cầu (S).
d) Sai. Ta có \(\overrightarrow {AB} = ( - 10;0;2)\), \(\overrightarrow {AC} = ( - 10;2;2)\).
Mặt phẳng (ABC) có vecto pháp tuyến là:
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&2\\2&2\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&{ - 10}\\2&{ - 10}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 10}&0\\{ - 10}&2\end{array}} \right|} \right) = \left( { - 4;0; - 20} \right)\).
Phương trình mặt phẳng (ABC) là \( - 4\left( {x - 0} \right) + 0\left( {y - 1} \right) - 20\left( {z - 4} \right) = 0\)
\( \Leftrightarrow - 4x - 20z + 80 = 0 \Leftrightarrow x + 5z - 20 = 0\).
Ta có \(d\left( {I,(ABC)} \right) = \frac{{\left| {1.( - 2) + 0.1 + 5.5 - 20} \right|}}{{\sqrt {{1^2} + {0^2} + {5^2}} }} = \frac{{3\sqrt {26} }}{{26}}\).
Vậy (S) cắt mặt phẳng (ABC) theo giao tuyến là đường tròn có bán kính:
\(\sqrt {{R^2} - {d^2}\left( {I,(ABC)} \right)} = \sqrt {9 - \frac{9}{{26}}} = \frac{{15\sqrt {26} }}{{26}}\).
Một chiếc xe đua F1 đạt tới vận tốc lớn nhất là 360 km/h. Đồ thị bên biểu thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol đỉnh tại gốc tọa độ O, giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trục tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu mét?

Lập phương trình 3 đồ thị biểu diễn vận tốc của xe rồi áp dụng tích phân tính quãng đường.
Đổi: 360 km/h = 100 m/s.
Gọi parabol biểu diễn vận tốc trong 2 giây đầu là \(y = a{t^2} + bt + c\) (a > 0).
Parabol đi qua điểm có tọa độ (0;0), (2;60) và đỉnh có tọa độ (0;0), do đó ta có hệ:
\(\left\{ \begin{array}{l}0 = a{.0^2} + b.0 + c\\60 = a{.2^2} + b.2 + c\\ - \frac{b}{{2a}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 = c\\60 = 4a + 2b + c\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 = c\\a = 15\\b = 0\end{array} \right. \Rightarrow y = v(t) = 15{t^2}\).
Gọi đường thẳng biểu diễn tốc độ từ giây thứ 2 đến giây thứ 3 là y = mt + n (m > 0).
Đường thẳng đi qua các điểm có tọa độ (2;60) và (3;360) nên ta có hệ:
\(\left\{ \begin{array}{l}60 = m.2 + n\\100 = m.3 + n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 40\\n = - 20\end{array} \right. \Rightarrow y = v(t) = 40t - 20\).
Đường thẳng biểu diễn tốc độ từ giây thứ 3 đến giây thứ 5 là y = v(t) = 100.
Vậy trong 5 giây đầu, xe đi được quãng đường là:
\(S = \int\limits_0^2 {15{t^2}dt} + \int\limits_2^3 {(40t - 20)dt} + \int\limits_3^5 {100dt} = 320\) (m).
Trong không gian Oxyz, cho điểm A(1;-1;2), mặt phẳng (P): x + y – 2z + 5 = 0 và đường thẳng d: \(\frac{{x + 1}}{2} = \frac{y}{1} = \frac{{z - 2}}{1}\). Đường thẳng \(\Delta \) cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Phương trình đường thẳng \(\Delta \) có dạng \(\frac{{x + 9}}{a} = \frac{{y - {y_0}}}{3} = \frac{{z - {z_0}}}{b}\) với \(ab \ne 0\). Tính \({a^2} + {b^2} + {y_0}^2 + {z_0}^2\).
Tìm tọa độ của M, N theo tham số t. Tìm t, vecto chỉ phương và một điểm \(\Delta \) đi qua để lập phương trình \(\Delta \).
Phương trình của d viết dưới dạng chứa tham số là \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = t\\z = 2 + t\end{array} \right.\) \((t \in \mathbb{R})\).
Vì M thuộc d nên \(M( - 1 + 2t;t;2 + t)\).
Mặt khác, A là trung điểm của MN nên ta có:
\(\left\{ \begin{array}{l}{x_A} = \frac{{{x_M} + {x_N}}}{2}\\{y_A} = \frac{{{y_M} + {y_N}}}{2}\\{z_A} = \frac{{{z_M} + {z_N}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = 2{x_A} - {x_M} = 2.1 - ( - 1 + 2t) = 3 - 2t\\{y_N} = 2{y_A} - {y_M} = 2.( - 1) - t = - 2 - t\\{z_N} = 2{z_A} - {z_M} = 2.2 - (2 + t) = 2 - t\end{array} \right. \Rightarrow N(3 - 2t; - 2 - t;2 - t)\).
Vì N thuộc mặt phẳng (P) nên thay tọa độ N vào phương trình của (P), ta được:
\((3 - 2t) + ( - 2 - t) - 2(2 - t) + 5 = 0 \Leftrightarrow t = 2\).
Do đó \(M(3;2;4)\), \(N( - 1; - 4;0)\), \(\overrightarrow {MN} = ( - 1 - 3; - 4 - 2;0 - 4) = ( - 4; - 6; - 4)\).
Gọi điểm thuộc \(\Delta \) có hoành độ là 9 là \(B\left( {9;{y_0};{z_0}} \right)\).
\(\Delta \) nhận \(\overrightarrow u = - \frac{1}{2}\overrightarrow {MN} = (2;3;2)\) làm vecto chỉ phương và đi qua điểm \(B\left( { - 9;{y_0};{z_0}} \right)\) có phương trình tham số:
\(\left\{ \begin{array}{l}x = - 9 + 2m\\y = {y_0} + 3m\\z = {z_0} + 2m\end{array} \right.\) \((m \in \mathbb{R})\).
Vì \(M(3;2;4)\) thuộc \(\Delta \) nên \(\left\{ \begin{array}{l}3 = - 9 + 2m\\2 = {y_0} + 3m\\4 = {z_0} + 2m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 6\\{y_0} = - 16\\{z_0} = - 8\end{array} \right. \Rightarrow B\left( { - 9; - 16; - 8} \right)\).
Vậy phương trình đường thẳng \(\Delta \) là \(\frac{{x + 9}}{2} = \frac{{y + 16}}{3} = \frac{{z + 8}}{2}\).
Ta có \({2^2} + {2^2} + {( - 16)^2} + {( - 8)^2} = 328\).
Hình bên vẽ minh họa mái hiên ABCD song song với mái nhà PQRS trong không gian với hệ tọa độ Oxyz (mái hiên và mái nhà đều phẳng) có Q(-10; 0; 200), P(-490; 0; 200), R(0; 1600; 0) và A(0; 0; -65). Mặt phẳng (ABCD) có phương trình y + az + 65a = 0. Tìm giá trị của a.

Tìm vecto pháp tuyến của (PQRS) bằng cách tính tích có hướng \(\left[ {\overrightarrow {PQ} ,\overrightarrow {PR} } \right]\).
Lập phương trình mặt phẳng (PQRS), từ đó lập phương trình (ABCD) song song với (PQRS) và đi qua A.
Ta có \(\overrightarrow {PQ} = ( - 10 + 490;0 - 0;200 - 200) = (480;0;0)\);
\(\overrightarrow {PR} = (0 + 490;1600 - 0;0 - 200) = (490;1600; - 200)\).
\(\left[ {\overrightarrow {PQ} ,\overrightarrow {PR} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&0\\{1600}&{ - 200}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{480}\\{ - 200}&{490}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{480}&0\\{490}&{1600}\end{array}} \right|} \right) = \left( {0;96000;768000} \right)\).
Suy ra một vecto pháp tuyến của (PQRS) là \(\overrightarrow {{n_{PQRS}}} = \frac{1}{{96000}}\left[ {\overrightarrow {PQ} ,\overrightarrow {PR} } \right] = \left( {0;1;8} \right)\).
Phương trình mặt phẳng (PQRS) là:
\(0\left( {x - 0} \right) + 1\left( {y - 1600} \right) + 8\left( {z - 0} \right) = 0 \Leftrightarrow y + 8z - 1600 = 0\).
Vì (ABCD) // (PQRS) nên phương trình của (ABCD) có dạng \(y + 8z + d = 0\).
A(0;0;-65) thuộc (ABCD) nên \(0 + 8.( - 65) + d = 0 \Leftrightarrow d = 520\).
Vậy (ABCD): \(y + 8z + 520 = 0\). Suy ra a = 8.
Trong một khoa cấp cứu của bệnh viện, người ta thống kê rằng 60% bệnh nhân bị chấn thương đầu là do tai nạn giao thông và còn lại là do tai nạn khác. Loại chấn thương đầu do tai nạn giao thông gây tử vong bệnh nhân chiếm 50% và loại chấn thương do tai nạn khác gây tử vong ở bệnh nhân chiếm 30%. Xác suất một bệnh án của bệnh nhân tử vong ở khoa cấp cứu đó bằng bao nhiêu?
Áp dụng công thức tính xác suất toàn phần.
Gọi các biến cố:
A: “Bệnh án của bệnh nhân bị chấn thương đầu do tai nạn giao thông”.
Suy ra \(\overline A \): “Bệnh án của bệnh nhân bị chấn thương đầu do tai nạn khác”.
B: “Bệnh án của bệnh nhân tử vong”.
Vì 60% bệnh nhân chấn thương đầu do tai nạn giao thông nên P(A) = 60% = 0,6, suy ra xác suất bệnh nhân chấn thương đầu do tai nạn khác là \(P(\overline A ) = 1 - P(A) = 1 - 0,6 = 0,4\).
Xác suất tử vong do chấn thương đầu vì tai nạn giao thông là 50%, do đó P(B|A) = 50% = 0,5.
Xác suất tử vong do chấn thương đầu vì tai nạn khác là 30%, do đó \(B(B|\overline A ) = 30\% = 0,3\).
Áp dụng công thức tính xác suất toàn phần, ta có xác suất một bệnh án của bệnh nhân tử vong ở khoa cấp cứu đó là:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A ) = 0,6.0,5 + 0,4.0,3 = 0,42\).
Tìm giao điểm của hàm số \(y = \sqrt {5 - x} \) với trục hoành.
Áp dụng công thức tính thể tích khối tròn xoay bằng tích phân.
Ta có \(\sqrt {5 - x} = 0 \Leftrightarrow x = 5\), do đó đồ thị hàm số \(y = \sqrt {5 - x} \) giao với trục hoành tại điểm có hoành độ bằng 0.
Thể tích khối tròn xoay khi quay D quanh trục Ox là:
\(V = \pi \int\limits_0^5 {{{\left( {\sqrt {5 - x} } \right)}^2}dx} = \int\limits_0^5 {\sqrt {5 - x} dx} = \pi \left( {5x - \frac{{{x^2}}}{2}} \right)\left| {\begin{array}{*{20}{c}}{^5}\\{_0}\end{array}} \right. = \frac{{25\pi }}{2} \approx 39,3\).
Gọi vecto chỉ phương của d, \(\Delta \) lần lượt là \(\overrightarrow {{u_d}} \), \(\overrightarrow {{u_\Delta }} \), vecto pháp tuyến của mặt phẳng (Oxy) là \(\overrightarrow n \).
Giải hệ \(\left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} .\overrightarrow {{u_d}} = 0\\\overrightarrow {{u_\Delta }} .\overrightarrow n = 0\end{array} \right.\)
Gọi vecto chỉ phương của d, \(\Delta \) lần lượt là \(\overrightarrow {{u_d}} = (2; - 1;3)\), \(\overrightarrow {{u_\Delta }} = ( - 1;b;c)\).
Vecto pháp tuyến của mặt phẳng (Oxy) là \(\overrightarrow n = (0;0;1)\).
Ta có \(\left\{ \begin{array}{l}\Delta \bot d\\\Delta //(Oxy)\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} .\overrightarrow {{u_d}} = 0\\\overrightarrow {{u_\Delta }} .\overrightarrow n = 0\end{array} \right.\). Do đó \(\overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{u_d}} ,\overrightarrow n } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 1}&3\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&2\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&{ - 1}\\0&0\end{array}} \right|} \right) = ( - 1; - 2;0)\).
Vậy b + c = -2 + 0 = -2.
Áp dụng công thức nhân xác suất.

Gọi các biến cố:
X: “Viên bi lấy ra từ hộp 1 có màu xanh”.
Y: “Viên bi lấy ra từ hộp 2 có màu xanh”.
TH1: Lấy được 2 bi xanh:
+ Công đoạn 1: Lấy bi xanh trong hộp 1: \(P(X) = \frac{4}{{10}} = \frac{2}{5}\).
+ Công đoạn 2: Lấy bi xanh trong hộp 2 sau khi có thêm 1 bi xanh từ hộp 1: \(P(Y|X) = \frac{6}{{10}} = \frac{3}{5}\).
TH2: Lấy được 2 bi đỏ:
+ Công đoạn 1: Lấy bi đỏ trong hộp 1: \(P(\overline X ) = \frac{6}{{10}} = \frac{3}{5}\).
+ Công đoạn 2: Lấy bi đỏ trong hộp 2 sau khi có thêm 1 bi đỏ từ hộp 1: \(P(\overline Y |\overline X ) = \frac{5}{{10}} = \frac{1}{2}\).
Vậy \(P(B) = P(XY) + P(\overline X \overline Y ) = P(X).P(Y|X) + P(\overline X ).P(\overline Y |\overline X ) = \frac{2}{5}.\frac{3}{5} + \frac{3}{5}.\frac{1}{2} = 0,54\).
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.










Danh sách bình luận