Đề thi học kì 2 Toán 12 Cánh diều - Đề số 3
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Họ nguyên hàm của hàm số f(x) = 2x + 6 là
-
A.
\({x^2} + C\)
-
B.
\({x^2} + 6x + C\)
-
C.
\(2{x^2} + C\)
-
D.
\(2{x^2} + 6x + C\)
Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số \(y = {x^{2022}}\)?
-
A.
\(\frac{{{x^{2023}}}}{{2023}} + 1\)
-
B.
\(\frac{{{x^{2023}}}}{{2023}}\)
-
C.
\(2022{x^{2021}}\)
-
D.
\(\frac{{{x^{2023}}}}{{2023}} - 1\)
Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
-
A.
\({f_2}\left( x \right) = \frac{1}{{{{\sin }^2}x}}\)
-
B.
\({f_1}\left( x \right) = - \frac{1}{{{{\cos }^2}x}}\)
-
C.
\({f_4}\left( x \right) = \frac{1}{{{{\cos }^2}x}}\)
-
D.
\({f_3}\left( x \right) = - \frac{1}{{{{\sin }^2}x}}\)
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = 2{x^2} + x + 1\) và \(y = {x^2} + 3\) bằng
-
A.
\(\frac{9}{2}\)
-
B.
\(\frac{5}{2}\)
-
C.
\(4\)
-
D.
\(2\)
Trong không gian Oxyz, cho đường thẳng d: \(\frac{{x + 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\). Vecto nào dưới đây là một vecto chỉ phương của d?
-
A.
\(\overrightarrow {{u_1}} = (2;1;1)\)
-
B.
\(\overrightarrow {{u_2}} = (1;2; - 3)\)
-
C.
\(\overrightarrow {{u_3}} = (1; - 2; - 1)\)
-
D.
\(\overrightarrow {{u_4}} = (2;1; - 3)\)
Trong không gian Oxyz, mặt phẳng (P): -2x + 5y + z – 3 = 0 có một vecto pháp tuyến là
-
A.
\(\overrightarrow {{n_1}} = \left( { - 2;5;1} \right)\)
-
B.
\(\overrightarrow {{n_2}} = \left( {2;5;1} \right)\)
-
C.
\(\overrightarrow {{n_3}} = \left( {2;5; - 1} \right)\)
-
D.
\(\overrightarrow {{n_4}} = \left( {2; - 5;1} \right)\)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(3;-1;4) và nhận vecto \(\overrightarrow u = ( - 2;4;5)\) làm vecto chỉ phương. Phương trình tham số của d là
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x = - 2 + 3t}\\{y = 4 - t}\\{z = 5 + 4t}\end{array}} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = - 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 - 2t}\\{y = 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 - 2t}\\{y = - 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\)
Trong không gian Oxyz, tính cosin của góc giữa hai đường thẳng \({d_1}:\frac{x}{2} = \frac{y}{1} = \frac{z}{{ - 1}}\), \({d_2}:\frac{{x - 1}}{3} = \frac{{y - 1}}{3} = \frac{{z - 1}}{9}\).
-
A.
\( - \frac{1}{2}\)
-
B.
\(0\)
-
C.
\(1\)
-
D.
\(\frac{1}{2}\)
Trong không gian Oxyz, xác định tâm I và bán kính R của mặt cầu có phương trình \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 4\).
-
A.
I(3;-1;2); R = 2
-
B.
I(-3;1;-2); R = 2
-
C.
I(-3;1;-2); R = 4
-
D.
I(3;-1;2); R = 4
Mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): x – 2y – 2z – 2 = 0 có phương trình là
-
A.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\)
-
B.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\)
-
C.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 3\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\)
Cho hai biến cố A và B có P(A) = 0,8, P(B) = 0,5, P(AB) = 0,2. Xác suất của biến cố A với điều kiện B là
-
A.
0,4
-
B.
0,5
-
C.
0,25
-
D.
0,625
Cho \(P(A) = \frac{2}{5}\), \(P(B|A) = \frac{1}{3}\), \(P(B|\overline A ) = \frac{1}{4}\). Giá trị của P(B) là
-
A.
\(\frac{{19}}{{60}}\)
-
B.
\(\frac{{17}}{{60}}\)
-
C.
\(\frac{9}{{20}}\)
-
D.
\(\frac{7}{{30}}\)
Cho hàm số y = f(x) = 2x + 3. Biết F(x) là một nguyên hàm của f(x) trên K.
a) Biết F(1) = 2 thì \(F(x) = {x^2} + 3x + 2\).
b) Giá trị của \(\int\limits_0^2 {f(x)dx} - \int\limits_5^2 {f(x)dx} + \int\limits_{ - 1}^0 {f(x)dx} \) bằng 42.
c) Diện tích hình phẳng giới hạn bởi các đường y = f(x), trục hoành và x = -2, x = 1 bằng 6.
d) Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường y = f(x) và \(y = {x^2} - 2x + 6\) quanh trục Ox bằng \(\frac{{1556\pi }}{{15}}\).
Hải đăng là một ngọn tháp được thiết kế để chiếu sáng từ một hệ thống đèn và thấu kính hoặc thời xưa là chiếu sáng bằng lửa, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là một mét), coi một phần mặt biển được khảo sát là mặt phẳng (Oxy), trục Oz hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 50 mét so với mực nước biển, biết đỉnh ở vị trí I(21;35;50). Biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = 16\).
b) Người đi biển coi là một điểm ở vị trí D(5121;658;0) thì có thể nhìn thấy được ánh sáng của ngọn hải đăng trên.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 (làm tròn đến hàng phần mười của mét) giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển coi là một điểm từ vị trí D(5121;658;0) di chuyển theo đường thẳng đến chân ngọn hải đăng với tốc độ 7 hải lý/giờ (biết 1 hải lý bằng 1852 mét) thì mất 5,28 phút (kết quả làm tròn đến hàng phần trăm) để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
Một vật đang chuyển động đều với vận tốc \({v_0}\) (m/s) thì bắt đầu tăng tốc với gia tốc \(a(t) = {v_0}t + {t^2}\) \(\left( {m/{s^2}} \right)\), trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m. Tính vận tốc ban đầu \({v_0}\) (m/s) của vật (làm tròn đến hàng phần mười).
Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng (Oxy) trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí A(3;-2;3) đến vị trí B(8;8;0). Góc giữa đường bay (một phần của đường thẳng AB và sân bay (một phần của mặt phẳng (Oxy)) bằng \(\alpha \) độ. Khi đó, giá trị của bằng \(\alpha \) bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
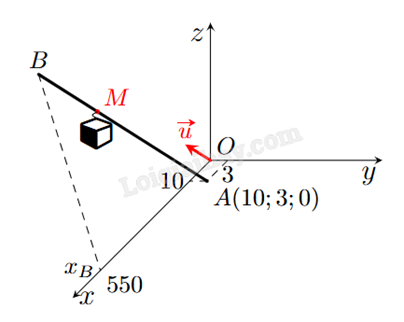
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cap có vecto chỉ phương là \(\overrightarrow u = (2; - 2;1)\) với tốc độ là 4,5 m/s (đơn vị trên mỗi trục tọa độ là mét). Sau thời gian 180 giây, cabin dừng ở điểm B. Tìm tung độ điểm B.
Có hai đội thi đấu môn bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I (làm tròn đến hai chữ số thập phân).
Lời giải và đáp án
Họ nguyên hàm của hàm số f(x) = 2x + 6 là
-
A.
\({x^2} + C\)
-
B.
\({x^2} + 6x + C\)
-
C.
\(2{x^2} + C\)
-
D.
\(2{x^2} + 6x + C\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {(2x + 6)dx} = 2.\frac{{{x^2}}}{2} + 6x + C = {x^2} + 6x + C\).
Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số \(y = {x^{2022}}\)?
-
A.
\(\frac{{{x^{2023}}}}{{2023}} + 1\)
-
B.
\(\frac{{{x^{2023}}}}{{2023}}\)
-
C.
\(2022{x^{2021}}\)
-
D.
\(\frac{{{x^{2023}}}}{{2023}} - 1\)
Đáp án : C
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {{x^{2022}}dx} = \frac{{{x^{2023}}}}{{2023}} + C\), với C là hằng số.
Do đó, các đáp án A, B, D đều là nguyên hàm của hàm số \(y = {x^{2022}}\).
Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
-
A.
\({f_2}\left( x \right) = \frac{1}{{{{\sin }^2}x}}\)
-
B.
\({f_1}\left( x \right) = - \frac{1}{{{{\cos }^2}x}}\)
-
C.
\({f_4}\left( x \right) = \frac{1}{{{{\cos }^2}x}}\)
-
D.
\({f_3}\left( x \right) = - \frac{1}{{{{\sin }^2}x}}\)
Đáp án : D
Áp dụng công thức nguyên hàm của hàm số lượng giác.
Có \(\int {\frac{1}{{{{\sin }^2}x}}dx} = - \cot x + C\) suy ra F(x) = cotx trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) là một nguyên hàm của hàm số \({f_3}\left( x \right) = - \frac{1}{{{{\sin }^2}x}}\).
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = 2{x^2} + x + 1\) và \(y = {x^2} + 3\) bằng
-
A.
\(\frac{9}{2}\)
-
B.
\(\frac{5}{2}\)
-
C.
\(4\)
-
D.
\(2\)
Đáp án : A
Áp dụng công thức tính diện tích hình phẳng: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \).
Phương trình hoành độ giao điểm: \(2{x^2} + x + 1 = {x^2} + 3 \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
Trên (-2;1) ta có \({x^2} + x - 2 < 0\) nên \(\left| {{x^2} + x - 2} \right| = - \left( {{x^2} + x - 2} \right)\).
Diện tích hình phẳng cần tìm là: \(\int\limits_{ - 2}^1 {\left| {{x^2} + x - 2} \right|dx} = - \int\limits_{ - 2}^1 {\left( {{x^2} + x - 2} \right)dx} = \frac{9}{2}\).
Trong không gian Oxyz, cho đường thẳng d: \(\frac{{x + 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\). Vecto nào dưới đây là một vecto chỉ phương của d?
-
A.
\(\overrightarrow {{u_1}} = (2;1;1)\)
-
B.
\(\overrightarrow {{u_2}} = (1;2; - 3)\)
-
C.
\(\overrightarrow {{u_3}} = (1; - 2; - 1)\)
-
D.
\(\overrightarrow {{u_4}} = (2;1; - 3)\)
Đáp án : C
Đường thẳng d: \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) có một vecto chỉ phương là \(\overrightarrow u = (a;b;c)\).
Đường thẳng d: \(\frac{{x + 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\) có một vecto chỉ phương là \(\overrightarrow u = ( - 1;2;1)\).
Ta có \(\overrightarrow {{u_3}} = (1; - 2; - 1) = - \overrightarrow u \) nên \(\overrightarrow {{u_3}} \) cùng phương với \(\overrightarrow u \), do đó cùng là một vecto chỉ phương của d.
Trong không gian Oxyz, mặt phẳng (P): -2x + 5y + z – 3 = 0 có một vecto pháp tuyến là
-
A.
\(\overrightarrow {{n_1}} = \left( { - 2;5;1} \right)\)
-
B.
\(\overrightarrow {{n_2}} = \left( {2;5;1} \right)\)
-
C.
\(\overrightarrow {{n_3}} = \left( {2;5; - 1} \right)\)
-
D.
\(\overrightarrow {{n_4}} = \left( {2; - 5;1} \right)\)
Đáp án : A
Mặt phẳng Ax + By + Cz + D = 0 có một vecto pháp tuyến là \(\overrightarrow n = (A;B;C)\).
Mặt phẳng (P): -2x + 5y + z – 3 = 0 có một vecto pháp tuyến là \(\overrightarrow {{n_1}} = \left( { - 2;5;1} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(3;-1;4) và nhận vecto \(\overrightarrow u = ( - 2;4;5)\) làm vecto chỉ phương. Phương trình tham số của d là
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x = - 2 + 3t}\\{y = 4 - t}\\{z = 5 + 4t}\end{array}} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = - 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 - 2t}\\{y = 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 - 2t}\\{y = - 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\)
Đáp án : D
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) có phương trình là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
d đi qua điểm M(3;-1;4) có vecto chỉ phương \(\overrightarrow u = ( - 2;4;5)\) có phương trình là \(\left\{ {\begin{array}{*{20}{c}}{x = 3 - 2t}\\{y = - 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\).
Trong không gian Oxyz, tính cosin của góc giữa hai đường thẳng \({d_1}:\frac{x}{2} = \frac{y}{1} = \frac{z}{{ - 1}}\), \({d_2}:\frac{{x - 1}}{3} = \frac{{y - 1}}{3} = \frac{{z - 1}}{9}\).
-
A.
\( - \frac{1}{2}\)
-
B.
\(0\)
-
C.
\(1\)
-
D.
\(\frac{1}{2}\)
Đáp án : B
Hai đường thẳng \({d_1}\), \({d_2}\) có vecto pháp tuyến lần lượt là \(\overrightarrow u \), \(\overrightarrow {u'} \) có \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {\overrightarrow u .\overrightarrow {u'} } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow {u'} } \right|}}\).
Vecto chỉ phương của \({d_1}\), \({d_2}\) lần lượt là \({\rm{\;}}\overrightarrow u = (2;1; - 1)\) và \(\overrightarrow {u'} {\rm{\;}} = (3;3;9)\).
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {2.3 + 1.3 - 1.9} \right|}}{{\sqrt {{2^2} + {1^2} + {{( - 1)}^2}} .\sqrt {{3^2} + {3^2} + {9^2}} }} = 0\).
Trong không gian Oxyz, xác định tâm I và bán kính R của mặt cầu có phương trình \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 4\).
-
A.
I(3;-1;2); R = 2
-
B.
I(-3;1;-2); R = 2
-
C.
I(-3;1;-2); R = 4
-
D.
I(3;-1;2); R = 4
Đáp án : A
Mặt cầu phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm I(a;b;c), bán kính R.
Mặt cầu phương trình \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 4\) có tâm I(3;-1;2), bán kính R = 2.
Mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): x – 2y – 2z – 2 = 0 có phương trình là
-
A.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\)
-
B.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\)
-
C.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 3\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\)
Đáp án : B
Bán kính mặt cầu là khoảng cách từ I đến (P). Từ đó lập phương trình mặt cầu tâm I, bán kính \(R = d\left( {I,(P)} \right)\).
Bán kính mặt cầu là \(R = d\left( {I,(P)} \right) = \frac{{\left| {1.( - 1) - 2.2 - 2.1 - 2} \right|}}{{\sqrt {{1^2} + {{( - 2)}^2} + {{( - 2)}^2}} }} = 3\).
Mặt cầu (S) có tâm I(-1;2;1), bán kính R = 3 có phương trình là \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\).
Cho hai biến cố A và B có P(A) = 0,8, P(B) = 0,5, P(AB) = 0,2. Xác suất của biến cố A với điều kiện B là
-
A.
0,4
-
B.
0,5
-
C.
0,25
-
D.
0,625
Đáp án : A
Áp dụng công thức tính xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\).
Áp dụng công thức: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,2}}{{0,5}} = 0,4\).
Cho \(P(A) = \frac{2}{5}\), \(P(B|A) = \frac{1}{3}\), \(P(B|\overline A ) = \frac{1}{4}\). Giá trị của P(B) là
-
A.
\(\frac{{19}}{{60}}\)
-
B.
\(\frac{{17}}{{60}}\)
-
C.
\(\frac{9}{{20}}\)
-
D.
\(\frac{7}{{30}}\)
Đáp án : B
Áp dụng công thức tính xác suất toàn phần.
Ta có \(P(\overline A ) = 1 - P(A) = 1 - \frac{2}{5} = \frac{3}{5}\).
Áp dụng công thức xác suất toàn phần:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A ) = \frac{2}{5}.\frac{1}{3} + \frac{3}{5}.\frac{1}{4} = \frac{{17}}{{60}}\).
Cho hàm số y = f(x) = 2x + 3. Biết F(x) là một nguyên hàm của f(x) trên K.
a) Biết F(1) = 2 thì \(F(x) = {x^2} + 3x + 2\).
b) Giá trị của \(\int\limits_0^2 {f(x)dx} - \int\limits_5^2 {f(x)dx} + \int\limits_{ - 1}^0 {f(x)dx} \) bằng 42.
c) Diện tích hình phẳng giới hạn bởi các đường y = f(x), trục hoành và x = -2, x = 1 bằng 6.
d) Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường y = f(x) và \(y = {x^2} - 2x + 6\) quanh trục Ox bằng \(\frac{{1556\pi }}{{15}}\).
a) Biết F(1) = 2 thì \(F(x) = {x^2} + 3x + 2\).
b) Giá trị của \(\int\limits_0^2 {f(x)dx} - \int\limits_5^2 {f(x)dx} + \int\limits_{ - 1}^0 {f(x)dx} \) bằng 42.
c) Diện tích hình phẳng giới hạn bởi các đường y = f(x), trục hoành và x = -2, x = 1 bằng 6.
d) Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường y = f(x) và \(y = {x^2} - 2x + 6\) quanh trục Ox bằng \(\frac{{1556\pi }}{{15}}\).
Áp dụng công thức tính nguyên hàm của hàm số lũy thừa, tính chất của tích phân, ứng dụng tích phân tính diện tích hình phẳng, thể tích khối tròn xoay.
a) Sai. \(F(x) = \int {f(x)dx} = \int {(2x + 3)dx} = {x^2} + 3x + C\).
Ta có \(F(1) = 2 \Leftrightarrow {1^2} + 3.1 + C = 2 \Leftrightarrow C = - 2\).
Vậy \(F(x) = {x^2} + 3x - 2\).
b) Đúng. \(\int\limits_0^2 {f(x)dx} - \int\limits_5^2 {f(x)dx} + \int\limits_{ - 1}^0 {f(x)dx} = \int\limits_{ - 1}^0 {f(x)dx} + \int\limits_0^2 {f(x)dx} - \int\limits_5^2 {f(x)dx} \)
\( = \int\limits_{ - 1}^0 {f(x)dx} + \int\limits_0^2 {f(x)dx} + \int\limits_2^5 {f(x)dx} = \int\limits_{ - 1}^5 {f(x)dx} = F(5) - F( - 1) = 42\).
c) Sai. Với x < -1,5 thì 2x + 3 < 0, suy ra \(\left| {2x + 3} \right| = - (2x + 3)\).
Với x > -1,5 thì 2x + 3 > 0, suy ra \(\left| {2x + 3} \right| = 2x + 3\).
\(S = \int\limits_{ - 2}^1 {\left| {2x + 3} \right|dx} = - \int\limits_{ - 2}^{ - 1,5} {(2x + 3)dx} + \int\limits_{ - 1,5}^1 {(2x + 3)dx} = \frac{{13}}{2}\).
d) Sai. Phương trình hoành độ giao điểm:
\({x^2} - 2x + 6 = 2x + 3 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
\(V = \pi \int\limits_1^3 {\left| {{{(2x + 3)}^2} - {{({x^2} - 2x + 6)}^2}} \right|dx} = \frac{{88\pi }}{5}\).
Hải đăng là một ngọn tháp được thiết kế để chiếu sáng từ một hệ thống đèn và thấu kính hoặc thời xưa là chiếu sáng bằng lửa, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là một mét), coi một phần mặt biển được khảo sát là mặt phẳng (Oxy), trục Oz hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 50 mét so với mực nước biển, biết đỉnh ở vị trí I(21;35;50). Biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = 16\).
b) Người đi biển coi là một điểm ở vị trí D(5121;658;0) thì có thể nhìn thấy được ánh sáng của ngọn hải đăng trên.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 (làm tròn đến hàng phần mười của mét) giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển coi là một điểm từ vị trí D(5121;658;0) di chuyển theo đường thẳng đến chân ngọn hải đăng với tốc độ 7 hải lý/giờ (biết 1 hải lý bằng 1852 mét) thì mất 5,28 phút (kết quả làm tròn đến hàng phần trăm) để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
a) Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = 16\).
b) Người đi biển coi là một điểm ở vị trí D(5121;658;0) thì có thể nhìn thấy được ánh sáng của ngọn hải đăng trên.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 (làm tròn đến hàng phần mười của mét) giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển coi là một điểm từ vị trí D(5121;658;0) di chuyển theo đường thẳng đến chân ngọn hải đăng với tốc độ 7 hải lý/giờ (biết 1 hải lý bằng 1852 mét) thì mất 5,28 phút (kết quả làm tròn đến hàng phần trăm) để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
Áp dụng biểu thức tọa độ các phép toán trong không gian.
Đổi: 4 km = 4000 m.
a) Sai. Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = {4000^2}\).
b) Sai. Khoảng cách từ người đi biển đến đỉnh ngọn hải đăng là:
\(ID = \sqrt {{{\left( {{x_D} - {x_I}} \right)}^2} + {{\left( {{y_D} - {y_I}} \right)}^2} + {{\left( {{z_D} - {z_I}} \right)}^2}} \)
\(= \sqrt {{{\left( {5121 - 21} \right)}^2} + {{\left( {658 - 35} \right)}^2} + {{\left( {0 - 50} \right)}^2}} \approx 5138\) (m).
Vì ID > 4000 nên người đi biển không nhìn được ánh sáng của ngọn hải đăng.
c) Đúng. Bán kính vùng sáng trên mặt biển là: \(\sqrt {{{4000}^2} - {{50}^2}} \approx 3999,7\) (m).
d) Sai. Chân ngọn hải đăng là H(21;35;0).
Ta có \(DH = \sqrt {{{(21 - 5121)}^2} + {{(35 - 658)}^2} + {{(0 - 0)}^2}} = \sqrt {{{5100}^2} + {{623}^2}} \).
Khoảng cách từ người đó đến điểm đầu tiên nhìn thấy ánh sáng ngọn hải đăng là:
\(\sqrt {{{5100}^2} + {{623}^2}} - \sqrt {{{4000}^2} - {{50}^2}} \) (m).
Tốc độ di chuyển của người đó là 7 hải lý/giờ = 12964 mét/giờ.
Thời gian để người đó đến điểm đầu tiên nhìn thấy ánh sáng ngọn hải đăng là:
\(\frac{{\sqrt {{{5100}^2} + {{623}^2}} - \sqrt {{{4000}^2} - {{50}^2}} }}{{12964}}.60 \approx 5,27\) (phút).
Một vật đang chuyển động đều với vận tốc \({v_0}\) (m/s) thì bắt đầu tăng tốc với gia tốc \(a(t) = {v_0}t + {t^2}\) \(\left( {m/{s^2}} \right)\), trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m. Tính vận tốc ban đầu \({v_0}\) (m/s) của vật (làm tròn đến hàng phần mười).
Tìm phương trình vận tốc và phương trình quãng đường ứng dụng nguyên hàm.
Phương trình vận tốc: \(v(t) = \int {a(t)dt} = \int {({v_0}t + {t^2})dt} = {v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + C\).
Tại thời điểm t = 0: \(v(0) = {v_0} \Rightarrow {v_0} = {v_0}\frac{{{0^2}}}{2} + \frac{{{0^3}}}{3} + C \Rightarrow C = {v_0}\).
Quãng đường vật đi được trong 3 giây kể từ lúc bắt đầu tăng tốc là:
\(S = \int\limits_0^3 {v(t)dt} = \int\limits_0^3 {\left( {{v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + {v_0}} \right)dt} = {v_0}\frac{{{3^3}}}{6} + \frac{{{3^4}}}{{12}} + {v_0}.3 = \frac{{15}}{2}{v_0} + \frac{{27}}{4}\) (m).
Theo đề bài, quãng đường vật đi được trong 3 giây kể từ lúc bắt đầu tăng tốc là 100 m nên:
\(\frac{{15}}{2}{v_0} + \frac{{27}}{4} = 100 \Rightarrow {v_0} \approx 12,4\) (m/s).
Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng (Oxy) trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí A(3;-2;3) đến vị trí B(8;8;0). Góc giữa đường bay (một phần của đường thẳng AB và sân bay (một phần của mặt phẳng (Oxy)) bằng \(\alpha \) độ. Khi đó, giá trị của bằng \(\alpha \) bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
Giả sử \(\alpha \) là góc giữa đường thẳng d và mặt phẳng (P).
Đường thẳng d có vecto chỉ phương là \(\overrightarrow u \) và mặt phẳng (P) có vecto pháp tuyến là \(\overrightarrow n \).
Khi đó \(\sin \alpha = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}}\).
Đường thẳng AB có vectơ chỉ phương là \(\overrightarrow {AB} = (5;\,10;\, - 3)\), mặt phẳng (Oxy) có vectơ pháp tuyến là \(\vec n = (0\,;0\,;1)\).
Ta có: \(\sin \alpha = \frac{{\left| {5.0 + 10.0 - 3.1} \right|}}{{\sqrt {{5^2} + {{10}^2} + {{( - 3)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{3}{{\sqrt {134} }} \Rightarrow \alpha \approx {15^o}\).
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cap có vecto chỉ phương là \(\overrightarrow u = (2; - 2;1)\) với tốc độ là 4,5 m/s (đơn vị trên mỗi trục tọa độ là mét). Sau thời gian 180 giây, cabin dừng ở điểm B. Tìm tung độ điểm B.

Lập phương trình tham số của đường cáp, từ đó suy ra tọa độ điểm B theo tham số.
Tính quãng đường AB (dựa vào vận tốc, thời gian di chuyển) rồi tìm t.
Thay t, ta được tọa độ điểm B.
Phương trình đường cáp là: \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\) \((t \in \mathbb{R})\).
Điểm B thuộc đường cáp nên B(10 + 2t; 3 – 2t; t).
Cabin đi với tốc độ 4,5 m/s. Sau 180 giây, cabin đi được quãng đường 4,5.180 = 810 (m).
Khi đó, cabin dừng ở điểm B nên ta có AB = 810
\( \Leftrightarrow {\left( {10 + 2t - 10} \right)^2} + {\left( {3 - 2t - 3} \right)^2} + {\left( {t - 0} \right)^2} = {810^2}\)
\( \Leftrightarrow 4{t^2} + 4{t^2} + {t^2} = {810^2} \Leftrightarrow 9{t^2} = {810^2} \Leftrightarrow t = 270\).
Suy ra B(550; -537; 270). Vậy tung độ điểm B là -537.
Có hai đội thi đấu môn bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I (làm tròn đến hai chữ số thập phân).
Áp dụng công thức tính xác suất toàn phần và công thức Bayes.
Gọi các biến cố:
A: “Vận động viên được chọn thuộc đội I”.
Suy ra \(\overline A \): “Vận động viên được chọn thuộc đội II”.
B: “Vận động viên được chọn đạt huy chương vàng”.
Đội I có 5 vận động viên, đội II có 7 vận động viên (tổng hai đội là 12 vận động viên) nên ta có \(P(A) = \frac{5}{{12}}\); \(P(\overline A ) = \frac{7}{{12}}\).
Xác suất vận động viên thuộc đội I đạt huy chương vàng là 0,65 nên ta có \(P(B|A) = 0,65\).
Xác suất vận động viên thuộc đội II đạt huy chương vàng là 0,55 nên ta có \(P(B|\overline A ) = 0,65\).
Áp dụng công thức xác suất toàn phần, xác suất vận động viên được chọn đạt huy chương vàng là:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A ) = \frac{5}{{12}}.0,65 + \frac{7}{{12}}.0,55 = \frac{{71}}{{120}}\).
Áp dụng công thức Bayes, xác suất vận động viên đạt huy chương vàng thuộc đội I là:
\(P(A|B) = \frac{{P(A).P(B|A)}}{{P(B)}} = \frac{{\frac{5}{{12}}.0,65}}{{\frac{{71}}{{120}}}} = \frac{{65}}{{142}} \approx 0,46\).
Áp dụng công thức tính tích phân của hàm số lượng giác.
\(\int\limits_0^{\frac{\pi }{3}} {\left( {2\sin x + \cos x} \right)dx} = - 2\cos x + \sin x\left| {\begin{array}{*{20}{c}}{^{\frac{\pi }{3}}}\\{_0}\end{array}} \right. = - 2\cos \frac{\pi }{3} + \sin \frac{\pi }{3} - \left( { - 2\cos 0 + \sin 0} \right)\)
\( = - 2.\frac{1}{2} + \frac{{\sqrt 3 }}{2} - \left( { - 2.1 + 0} \right) = 1 + \frac{{\sqrt 3 }}{2} = \frac{{2 + \sqrt 3 }}{2}\).
Vậy S = a + b = 2 + 1 = 3.
Mặt phẳng \((\alpha )\) cắt các trục Ox, Oy, Oz lần lượt tại A(m;0;0), B(0;n;0), C(0;0;p), \(m,n,p \ne 0\).
Lập phương trình mặt chắn của \((\alpha )\) (1)
M là trực tâm tam giác ABC nên \(\left\{ \begin{array}{l}\overrightarrow {AM} .\overrightarrow {BC} = 0\\\overrightarrow {BM} .\overrightarrow {AC} = 0\end{array} \right.\) (2)
Từ (1) và (2), ta tìm được m, n, p. Đưa phương trình mặt chắn về dạng tổng quát, ta tìm được a, b, c.
Mặt phẳng \((\alpha )\) cắt các trục Ox, Oy, Oz lần lượt tại A(m;0;0), B(0;n;0), C(0;0;p), \(m,n,p \ne 0\). Ta có phương trình mặt phẳng \((\alpha )\) có dạng \(\frac{x}{m} + \frac{y}{n} + \frac{z}{p} = 1\).
Mà \(M \in (\alpha ) \Leftrightarrow \frac{1}{m} + \frac{2}{n} + \frac{3}{p} = 1\) (1)
Ta có \(\overrightarrow {AM} = (1 - m;2;3)\), \(\overrightarrow {BM} = (1;2 - n;3)\), \(\overrightarrow {BC} = (0; - n;p)\), \(\overrightarrow {AC} = ( - m;0;p)\).
M là trực tâm tam giác ABC nên \(\left\{ \begin{array}{l}\overrightarrow {AM} .\overrightarrow {BC} = 0\\\overrightarrow {BM} .\overrightarrow {AC} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3p - 2n = 0\\3p - m = 0\end{array} \right.\) (2)
Từ (1) và (2) suy ra: m = 14; n = 7; \(p = \frac{{14}}{3}\).
Suy ra \((\alpha )\) có phương trình \(\frac{x}{{14}} + \frac{y}{7} + \frac{{3z}}{{14}} = 1 \Leftrightarrow x + 2y + 3z - 14 = 0\).
Vậy T = a + b + c = 1 + 2 + 3 = 6.
Gọi x là tổng số kẹo trong túi.
Áp dụng công thức nhân xác suất để tìm x.
Gọi các biến cố:
A: “Lấy được kẹo màu cam lần thứ nhất”.
B: “Lấy được kẹo màu cam lần thứ hai”.
Gọi tổng số kẹo là x (chiếc; \(x \in \mathbb{N}\), x > 6).
Ban đầu, có 6 chiếc kẹo cam trong tổng số x chiếc kẹo nên xác suất lấy được kẹo cam lần đầu là \(P(A) = \frac{6}{x}\).
Sau đó, còn 5 chiếc kẹo cam trong tổng số x – 1 chiếc kẹo còn lại nên xác suất lấy được chiếc kẹo cam lần thứ hai (biết lần đầu đã lấy được kẹo cam) là \(P(B|A) = \frac{5}{{x - 1}}\).
Áp dụng công thức nhân xác suất, xác suất để lấy cả hai lần đều được kẹo cam là:
\(P(AB) = P(A).P(B|A) = \frac{6}{x}.\frac{5}{{x - 1}} = \frac{{30}}{{x(x - 1)}}\).
Theo đề bài: \(P(AB) = \frac{1}{3} \Leftrightarrow \frac{{30}}{{x(x - 1)}} = \frac{1}{3} \Leftrightarrow {x^2} - x - 90 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = - 9\end{array} \right.\)
Ta có x = 10 thỏa mãn điều kiện. Vậy ban đầu trong túi có 10 chiếc kẹo.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.










Danh sách bình luận