Đề thi giữa kì 2 Toán 12 Cánh diều - Đề số 5
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Hàm số \(F(x) = 2{x^9} + 2024\) là nguyên hàm của hàm số
-
A.
\(f(x) = 18{x^8}\)
-
B.
\(f(x) = 18{x^8} + 2024\)
-
C.
\(f(x) = 18{x^8} + C\)
-
D.
\(f(x) = \frac{{{x^{10}}}}{5} + 2024x\)
Hàm số F(x) = lnx là nguyên hàm của hàm số nào sau đây trên khoảng \(\left( {0; + \infty } \right)\)?
-
A.
\(f(x) = \frac{1}{{\left| x \right|}}\)
-
B.
\(f(x) = - \frac{1}{x}\)
-
C.
\(f(x) = \frac{1}{x}\)
-
D.
\(f(x) = \frac{1}{x} + C\)
Cho hàm số \(f(x) = {x^3} + 2\). Khẳng định nào sau đây đúng?
-
A.
\(\int {f(x)dx} = \frac{{{x^4}}}{4} + 2x + C\)
-
B.
\(\int {f(x)dx} = \frac{{{x^4}}}{4} + \frac{{{x^2}}}{2} + C\)
-
C.
\(\int {f(x)dx} = \frac{{{x^3}}}{3} + {x^2} + C\)
-
D.
\(\int {f(x)dx} = {x^4} + 2x + C\)
Cho F(x) là nguyên hàm của hàm số \(f(x) = 5{x^4} + \frac{1}{{{x^3}}}\) thỏa mãn F(1) = 0. Tìm F(x).
-
A.
\(F(x) = {x^5} - \frac{3}{{2{x^2}}} + \frac{1}{2}\)
-
B.
\(F(x) = {x^5} - \frac{3}{{{x^2}}} + 2\)
-
C.
\(F(x) = {x^5} - \frac{1}{{2{x^2}}} - \frac{1}{2}\)
-
D.
\(F(x) = {x^5} + \frac{1}{{2{x^2}}} - \frac{3}{2}\)
Điều kiện nào sau đây là cần thiết để hàm số f(x) có thể tính tích phân trên đoạn [a;b]?
-
A.
Hàm số f(x) phải liên tục trên đoạn [a;b].
-
B.
Hàm số f(x) phải có đạo hàm trên đoạn [a;b].
-
C.
Hàm số f(x) phải đồng biến trên đoạn [a;b].
-
D.
Hàm số f(x) phải là hàm số bậc hai trên đoạn [a;b].
Nếu F(x) là nguyên hàm của hàm số f(x), thì tích phân của f(x) trên đoạn [a;b] được tính như thế nào?
-
A.
\(F\left( b \right)--F\left( a \right)\)
-
B.
\(F\left( a \right)--F\left( b \right)\)
-
C.
\(\frac{{F(b)}}{{F(a)}}\)
-
D.
\(\frac{{F(a)}}{{F(b)}}\)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x + 2y – z + 5 = 0. Vecto nào sau đây là vecto pháp tuyến của mặt phẳng (P)?
-
A.
\(\overrightarrow {{n_1}} = (2; - 1;2)\)
-
B.
\(\overrightarrow {{n_2}} = (2; - 1;5)\)
-
C.
\(\overrightarrow {{n_3}} = (3;2;5)\)
-
D.
\(\overrightarrow {{n_4}} = (3;2; - 1)\)
Trong không gian Oxyz, cho A(1;1;-2), B(2;0;3), C(-2;4;1). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là
-
A.
\(2x - 2y + z + 2 = 0\)
-
B.
\(x + y - 2z - 6 = 0\)
-
C.
\(x + y - 2z + 2 = 0\)
-
D.
\(2x + 2y + z - 2 = 0\)
Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt phẳng (Oxz)?
-
A.
y = 0
-
B.
x = 0
-
C.
z = 0
-
D.
y – 1 = 0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(2;-1;5) và nhận vecto \(\overrightarrow u = (2;3;1)\) làm vecto chỉ phương. Phương trình tham số của d là
-
A.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3 - t\\z = - 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 1 - 3t\\z = 5 - t\end{array} \right.\) \((t \in \mathbb{R})\)
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x – 3y + 4z + 20 = 0 và (Q): 4x – 13y – 6z + 40 = 40. Mệnh đề nào sau đây đúng?
-
A.
(P) // (Q)
-
B.
(P) \( \equiv \) (Q)
-
C.
(P) cắt (Q)
-
D.
(P) \( \bot \) (Q)
Trong không gian Oxyz, cho mặt cầu có phương trình \({\left( {x + 2} \right)^2} + {\left( {y - 7} \right)^2} + {\left( {z + 6} \right)^2} = 9\). Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
-
A.
I(-2;-7;-6); R = 3
-
B.
I(-2;7;-6); R = 9
-
C.
I(-2;7;-6); R = 3
-
D.
I(2;-7;6); R = 9
Cho hàm số \(y = {e^x}\).
a) Diện tích hình phẳng được giới hạn bởi hàm số đã cho với trục hoành, đường thẳng x = -1, x = 1 là \(\frac{{{e^2} - 1}}{e}\).
b) Với a = ln4 thì diện tích hình phẳng được giới hạn bởi hàm số đã cho với các trục toạ độ và đường thẳng x = a bằng 3.
c) Cho hình phẳng D giới hạn bởi đường cong \(y = {e^x}\), trục hoành và các đường thẳng x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng \(2\pi \frac{{{e^2} - 1}}{2}\).
d) Gọi d là tiếp tuyến của đồ thị hàm số \(y = {e^x}\) đã cho tại điểm \({x_0} = 0\). Diện tích hình phẳng được giới hạn bởi đường thẳng d với trục hoành, đường thẳng x = -1 và x = 1 là 2.
Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng (P): x – 2y + 2z – 1 = 0, (Q): x – 2y + 2z – 3 = 0 và điểm A(1;1;-2).
a) Hai mặt phẳng (P ) và (Q) song song với nhau.
b) \(d\left( {A,(P)} \right) = 1\).
c) \(d\left( {(P),(Q)} \right) = \frac{2}{3}\).
d) Phương trình mặt phẳng song song cách đều (P) và (Q) là x – 2y + 2z + 2 = 0.
Giả sử \(\forall a,b \in \mathbb{R}\), a < 0 < b, \(\int\limits_a^b {\left| {{x^7}} \right|dx} = m{a^8} + n{b^8}\) trong đó m, n là các hằng số thực (không phụ thuộc vào a và b). Giá trị của biểu thức P = m − 5n là bao nhiêu?
Đáp án:
Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = −12t + 36 (m/s) trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được quãng đường là s mét. Tính giá trị của s.
Đáp án:
Cho điểm A(1;2;−1) và mặt phẳng \(\left( \alpha \right)\): x – 2y + 2z + 2 = 0. Mặt phẳng \(\left( \beta \right)\) song song với mặt phẳng \(\left( \alpha \right)\) và cách A một khoảng 1 có dạng \(\left( \beta \right)\): x – by + cz + d = 0. Khi đó S = 3b – c + d bằng bao nhiêu?
Đáp án:
Gọi m, n là hai giá trị thực thỏa mãn giao tuyến của hai mặt phẳng \(({P_m})\): mx + 2y + nz + 1 = 0 và \(({Q_m})\): x – my + nz + 2 = 0 vuông góc với mặt phẳng \((\alpha )\): 4x – y – 6z + 3 = 0. Tính m + n.
Đáp án:
Lời giải và đáp án
Hàm số \(F(x) = 2{x^9} + 2024\) là nguyên hàm của hàm số
-
A.
\(f(x) = 18{x^8}\)
-
B.
\(f(x) = 18{x^8} + 2024\)
-
C.
\(f(x) = 18{x^8} + C\)
-
D.
\(f(x) = \frac{{{x^{10}}}}{5} + 2024x\)
Đáp án : A
F(x) là nguyên hàm của hàm số f(x) nếu F’(x) = f(x).
\(F'(x) = \left( {2{x^9} + 2024} \right)' = 18{x^8}\).
Hàm số F(x) = lnx là nguyên hàm của hàm số nào sau đây trên khoảng \(\left( {0; + \infty } \right)\)?
-
A.
\(f(x) = \frac{1}{{\left| x \right|}}\)
-
B.
\(f(x) = - \frac{1}{x}\)
-
C.
\(f(x) = \frac{1}{x}\)
-
D.
\(f(x) = \frac{1}{x} + C\)
Đáp án : C
F(x) là nguyên hàm của hàm số f(x) nếu F’(x) = f(x).
\(F'(x) = \left( {\ln x} \right)' = \frac{1}{x}\).
Cho hàm số \(f(x) = {x^3} + 2\). Khẳng định nào sau đây đúng?
-
A.
\(\int {f(x)dx} = \frac{{{x^4}}}{4} + 2x + C\)
-
B.
\(\int {f(x)dx} = \frac{{{x^4}}}{4} + \frac{{{x^2}}}{2} + C\)
-
C.
\(\int {f(x)dx} = \frac{{{x^3}}}{3} + {x^2} + C\)
-
D.
\(\int {f(x)dx} = {x^4} + 2x + C\)
Đáp án : A
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {f(x)dx} = \int {\left( {{x^3} + 2} \right)} = \frac{{{x^4}}}{4} + 2x + C\).
Cho F(x) là nguyên hàm của hàm số \(f(x) = 5{x^4} + \frac{1}{{{x^3}}}\) thỏa mãn F(1) = 0. Tìm F(x).
-
A.
\(F(x) = {x^5} - \frac{3}{{2{x^2}}} + \frac{1}{2}\)
-
B.
\(F(x) = {x^5} - \frac{3}{{{x^2}}} + 2\)
-
C.
\(F(x) = {x^5} - \frac{1}{{2{x^2}}} - \frac{1}{2}\)
-
D.
\(F(x) = {x^5} + \frac{1}{{2{x^2}}} - \frac{3}{2}\)
Đáp án : C
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
Sử dụng điều kiện đề bài cho F(1) = 0 để tìm C.
\(F(x) = \int {f(x)dx} = \int {\left( {5{x^4} + \frac{1}{{{x^3}}}} \right)dx} = {x^5} + \frac{{{x^{ - 2}}}}{{ - 2}} + C = {x^5} - \frac{1}{{2{x^2}}} + C\).
\(F(1) = 0 \Leftrightarrow {1^5} - \frac{1}{{{{2.1}^2}}} + C = 0 \Leftrightarrow C = - \frac{1}{2}\).
Vậy \(F(x) = {x^5} - \frac{1}{{2{x^2}}} + C\).
Điều kiện nào sau đây là cần thiết để hàm số f(x) có thể tính tích phân trên đoạn [a;b]?
-
A.
Hàm số f(x) phải liên tục trên đoạn [a;b].
-
B.
Hàm số f(x) phải có đạo hàm trên đoạn [a;b].
-
C.
Hàm số f(x) phải đồng biến trên đoạn [a;b].
-
D.
Hàm số f(x) phải là hàm số bậc hai trên đoạn [a;b].
Đáp án : A
Dựa vào định nghĩa tích phân.
Hàm số f(x) phải liên tục trên đoạn [a;b].
Nếu F(x) là nguyên hàm của hàm số f(x), thì tích phân của f(x) trên đoạn [a;b] được tính như thế nào?
-
A.
\(F\left( b \right)--F\left( a \right)\)
-
B.
\(F\left( a \right)--F\left( b \right)\)
-
C.
\(\frac{{F(b)}}{{F(a)}}\)
-
D.
\(\frac{{F(a)}}{{F(b)}}\)
Đáp án : A
Áp dụng định nghĩa tích phân.
\(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x + 2y – z + 5 = 0. Vecto nào sau đây là vecto pháp tuyến của mặt phẳng (P)?
-
A.
\(\overrightarrow {{n_1}} = (2; - 1;2)\)
-
B.
\(\overrightarrow {{n_2}} = (2; - 1;5)\)
-
C.
\(\overrightarrow {{n_3}} = (3;2;5)\)
-
D.
\(\overrightarrow {{n_4}} = (3;2; - 1)\)
Đáp án : D
Mặt phẳng (P): Ax + By + Cz + D = 0 có vecto pháp tuyến là \(\overrightarrow n = (A;B;C)\).
Vecto pháp tuyến của mặt phẳng (P) là \(\overrightarrow {{n_4}} = (3;2; - 1)\).
Trong không gian Oxyz, cho A(1;1;-2), B(2;0;3), C(-2;4;1). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là
-
A.
\(2x - 2y + z + 2 = 0\)
-
B.
\(x + y - 2z - 6 = 0\)
-
C.
\(x + y - 2z + 2 = 0\)
-
D.
\(2x + 2y + z - 2 = 0\)
Đáp án : A
Mặt phẳng qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} \) làm vecto pháp tuyến.
Mặt phẳng qua A(1;1;-2) và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} = ( - 4;4; - 2)\) làm vecto pháp tuyến có phương trình là:
\( - 4(x - 1) + 4(y - 1) - 2(z + 2) = 0 \Leftrightarrow - 4x + 4y - 2z - 4 = 0 \Leftrightarrow 2x - 2y - z + 2 = 0\).
Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt phẳng (Oxz)?
-
A.
y = 0
-
B.
x = 0
-
C.
z = 0
-
D.
y – 1 = 0
Đáp án : A
Tìm vecto pháp tuyến và một điểm mặt phẳng đi qua.
Mặt phẳng (Oxz) nhận \(\overrightarrow j = (0;1;0)\) làm vecto pháp tuyến và đi qua gốc tọa độ O nên có phương trình tổng quát là \(0(x - 0) + 1(y - 0) + 0(z - 0) = 0 \Leftrightarrow y = 0\).
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(2;-1;5) và nhận vecto \(\overrightarrow u = (2;3;1)\) làm vecto chỉ phương. Phương trình tham số của d là
-
A.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3 - t\\z = - 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 1 - 3t\\z = 5 - t\end{array} \right.\) \((t \in \mathbb{R})\)
Đáp án : C
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) có phương trình là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
d đi qua điểm M(2;-1;5) có vecto chỉ phương \(\overrightarrow u = (2;3;1)\) có phương trình là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in \mathbb{R})\).
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x – 3y + 4z + 20 = 0 và (Q): 4x – 13y – 6z + 40 = 40. Mệnh đề nào sau đây đúng?
-
A.
(P) // (Q)
-
B.
(P) \( \equiv \) (Q)
-
C.
(P) cắt (Q)
-
D.
(P) \( \bot \) (Q)
Đáp án : C
So sánh tỉ lệ các hệ số và áp dụng công thức tính tích vô hướng của hai vecto.
Ta có \(\frac{2}{4} \ne \frac{{ - 3}}{{ - 13}} \ne \frac{4}{{ - 6}}\) và \(2.4 - 3.( - 13) + 4.( - 6) = 23\) nên (P) cắt (Q).
Trong không gian Oxyz, cho mặt cầu có phương trình \({\left( {x + 2} \right)^2} + {\left( {y - 7} \right)^2} + {\left( {z + 6} \right)^2} = 9\). Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
-
A.
I(-2;-7;-6); R = 3
-
B.
I(-2;7;-6); R = 9
-
C.
I(-2;7;-6); R = 3
-
D.
I(2;-7;6); R = 9
Đáp án : C
Mặt cầu phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm I(a;b;c), bán kính R.
Mặt cầu phương trình \({\left( {x + 2} \right)^2} + {\left( {y - 7} \right)^2} + {\left( {z + 6} \right)^2} = 9\) có tâm I(-2;7;-6), bán kính R = 3.
Cho hàm số \(y = {e^x}\).
a) Diện tích hình phẳng được giới hạn bởi hàm số đã cho với trục hoành, đường thẳng x = -1, x = 1 là \(\frac{{{e^2} - 1}}{e}\).
b) Với a = ln4 thì diện tích hình phẳng được giới hạn bởi hàm số đã cho với các trục toạ độ và đường thẳng x = a bằng 3.
c) Cho hình phẳng D giới hạn bởi đường cong \(y = {e^x}\), trục hoành và các đường thẳng x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng \(2\pi \frac{{{e^2} - 1}}{2}\).
d) Gọi d là tiếp tuyến của đồ thị hàm số \(y = {e^x}\) đã cho tại điểm \({x_0} = 0\). Diện tích hình phẳng được giới hạn bởi đường thẳng d với trục hoành, đường thẳng x = -1 và x = 1 là 2.
a) Diện tích hình phẳng được giới hạn bởi hàm số đã cho với trục hoành, đường thẳng x = -1, x = 1 là \(\frac{{{e^2} - 1}}{e}\).
b) Với a = ln4 thì diện tích hình phẳng được giới hạn bởi hàm số đã cho với các trục toạ độ và đường thẳng x = a bằng 3.
c) Cho hình phẳng D giới hạn bởi đường cong \(y = {e^x}\), trục hoành và các đường thẳng x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng \(2\pi \frac{{{e^2} - 1}}{2}\).
d) Gọi d là tiếp tuyến của đồ thị hàm số \(y = {e^x}\) đã cho tại điểm \({x_0} = 0\). Diện tích hình phẳng được giới hạn bởi đường thẳng d với trục hoành, đường thẳng x = -1 và x = 1 là 2.
a, b) Áp dụng công thức tính diện tích của hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
c) Áp dụng công thức tính thể tích khối tròn xoay \(V = \pi \int\limits_a^b {{f^2}(x)dx} \).
d) Áp dụng quy tắc lập phương trình tiếp tuyến của hàm số y = f(x) tại điểm \({x_0}\): \(y = f'({x_0})(x - {x_0}) + f({x_0})\).
Áp dụng công thức tính diện tích của hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
a) Đúng. \({S_1} = \int\limits_{ - 1}^1 {\left| {{e^x}} \right|dx} = \int\limits_{ - 1}^1 {{e^x}dx} = {e^x}\left| {\begin{array}{*{20}{c}}{^1}\\{_{ - 1}}\end{array}} \right. = {e^1} - {e^{ - 1}} = e - \frac{1}{e} = \frac{{{e^2} - 1}}{e}\).
b) Đúng. \({S_2} = \int\limits_0^{\ln 4} {\left| {{e^x}} \right|dx} = \int\limits_0^{\ln 4} {{e^x}dx} = {e^x}\left| {\begin{array}{*{20}{c}}{^{\ln 4}}\\{_0}\end{array}} \right. = {e^{\ln 4}} - {e^0} = 4 - 1 = 3\).
c) Sai. \(V = \pi \int\limits_0^1 {{{\left( {{e^x}} \right)}^2}dx} = \pi \int\limits_0^1 {{{\left( {{e^2}} \right)}^x}dx} = \pi .\frac{{{e^{2x}}}}{{\ln {e^2}}}\left| {\begin{array}{*{20}{c}}{^1}\\{_0}\end{array}} \right. = \pi .\frac{{{e^{2x}}}}{2}\left| {\begin{array}{*{20}{c}}{^1}\\{_0}\end{array}} \right. = \frac{{\pi {e^2}}}{2} - \frac{\pi }{2} = \pi \frac{{{e^2} - 1}}{2}\).
d) Đúng. \(f'(x) = \left( {{e^x}} \right)' = {e^x} \Rightarrow f'(0) = {e^0} = 1\); \(f(0) = {e^0} = 1\).
Phương trình tiếp tuyến cần tìm là \(y = 1(x - 0) + 1 \Leftrightarrow y = x + 1\).
Trên đoạn [-1;1] thấy \(x + 1 \ge 0\) nên ta có:
\({S_3} = \int\limits_{ - 1}^1 {\left| {x + 1} \right|dx} = \int\limits_{ - 1}^1 {\left( {x + 1} \right)dx} = \left( {\frac{{{x^2}}}{2} + x} \right)\left| {\begin{array}{*{20}{c}}{^1}\\{_{ - 1}}\end{array}} \right. = \frac{{{1^2}}}{2} + 1 - \frac{{{{( - 1)}^2}}}{2} - ( - 1) = 2\).
Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng (P): x – 2y + 2z – 1 = 0, (Q): x – 2y + 2z – 3 = 0 và điểm A(1;1;-2).
a) Hai mặt phẳng (P ) và (Q) song song với nhau.
b) \(d\left( {A,(P)} \right) = 1\).
c) \(d\left( {(P),(Q)} \right) = \frac{2}{3}\).
d) Phương trình mặt phẳng song song cách đều (P) và (Q) là x – 2y + 2z + 2 = 0.
a) Hai mặt phẳng (P ) và (Q) song song với nhau.
b) \(d\left( {A,(P)} \right) = 1\).
c) \(d\left( {(P),(Q)} \right) = \frac{2}{3}\).
d) Phương trình mặt phẳng song song cách đều (P) và (Q) là x – 2y + 2z + 2 = 0.
Xác định vecto pháp tuyến của hai mặt phẳng. Áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
Vecto pháp tuyến của mặt phẳng (P) và (Q) lần lượt là \(\overrightarrow {{n_P}} = (1; - 2;2)\), \(\overrightarrow {{n_Q}} = (1; - 2;2)\).
a) Đúng. Ta có \(\frac{1}{1} = \frac{{ - 2}}{{ - 2}} = \frac{2}{2} \ne \frac{{ - 1}}{{ - 3}}\) nên hai mặt phẳng (P) và (Q) song song với nhau.
b) Sai. \(d\left( {A,(P)} \right) = \frac{{\left| {1.1 - 2.1 + 2.( - 2) - 1} \right|}}{{\sqrt {{1^2} + {{( - 2)}^2} + {2^2}} }} = 2\).
c) Đúng. B(1;0;0) là một điểm thuộc (P).
Vì (P) // (Q) nên \(d\left( {(P),(Q)} \right) = d\left( {B,(Q)} \right) = \frac{{\left| {1.1 - 2.0 + 2.0 - 3} \right|}}{{\sqrt {{1^2} + {{( - 2)}^2} + {2^2}} }} = \frac{2}{3}\).
d) Sai. Gọi d là đường thẳng đi qua B và vuông góc với (Q).
Phương trình của d là \(\left\{ \begin{array}{l}x = 1 + t\\y = - 2t\\z = 2t\end{array} \right.\), \(t \in \mathbb{R}\).
Thay x, y, z của phương trình đường thẳng d vào phương trình mặt phẳng (Q), ta có:
\(1 + t - 2.( - 2t) + 2.2t - 3 = 0 \Leftrightarrow 9t - 2 = 0 \Leftrightarrow t = \frac{2}{9}\).
Do đó, giao điểm C của d với (Q) có tọa độ \(C\left( {\frac{{11}}{9}; - \frac{4}{9};\frac{4}{9}} \right)\).
Trung điểm của BC là \(I\left( {\frac{{10}}{9}; - \frac{2}{4};\frac{2}{4}} \right)\).
Mặt phẳng song song cách đều (P) và (Q) đi qua I và có vecto pháp tuyến trùng với vecto pháp tuyến của (P), (Q) nên có phương trình tổng quát:
\(1\left( {x - \frac{{10}}{9}} \right) - 2\left( {y + \frac{2}{9}} \right) + 2\left( {z - \frac{2}{9}} \right) = 0 \Leftrightarrow x - 2y + 2z - 2 = 0\).
Giả sử \(\forall a,b \in \mathbb{R}\), a < 0 < b, \(\int\limits_a^b {\left| {{x^7}} \right|dx} = m{a^8} + n{b^8}\) trong đó m, n là các hằng số thực (không phụ thuộc vào a và b). Giá trị của biểu thức P = m − 5n là bao nhiêu?
Đáp án:
Đáp án:
Xét dấu trên đoạn [a;b] để phá dấu trị tuyệt đối.
\(\int\limits_a^b {\left| {{x^7}} \right|dx} = \int\limits_a^0 {\left| {{x^7}} \right|dx} + \int\limits_0^b {\left| {{x^7}} \right|dx} = - \int\limits_a^0 {{x^7}dx} + \int\limits_0^b {{x^7}dx} = - \frac{{{x^8}}}{8}\left| {\begin{array}{*{20}{c}}{^0}\\{_a}\end{array}} \right. + \frac{{{x^8}}}{8}\left| {\begin{array}{*{20}{c}}{^b}\\{_0}\end{array}} \right. = \frac{{{a^8}}}{8} + \frac{{{b^8}}}{8} = \frac{1}{8}{a^8} + \frac{1}{8}{b^8}\).
Suy ra \(m = \frac{1}{8}\), \(n = \frac{1}{8} \Rightarrow m - 5n = \frac{1}{8} - 5.\frac{1}{8} = - \frac{1}{2} = - 0.5\).
Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = −12t + 36 (m/s) trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được quãng đường là s mét. Tính giá trị của s.
Đáp án:
Đáp án:
Tìm \({t_0}\) sao cho \(v({t_0}) = 0\). Tính \(\int\limits_0^{{t_0}} {v(t)dt} \).
Ô tô dừng hẳn thì v(t) = 0. Thời gian để ô tô dừng hẳn kể từ lúc đạp phanh là:
\(v(t) = 0 \Leftrightarrow - 12t + 36 = 0 \Leftrightarrow t = 3\) (s).
Quãng đường ô tô đi được trong 3 giây đó đến khi dừng hẳn là:
\(s = \int\limits_0^3 {v(t)dt} = \int\limits_0^3 {\left( { - 12t + 36} \right)dt} = 54\) (m).
Cho điểm A(1;2;−1) và mặt phẳng \(\left( \alpha \right)\): x – 2y + 2z + 2 = 0. Mặt phẳng \(\left( \beta \right)\) song song với mặt phẳng \(\left( \alpha \right)\) và cách A một khoảng 1 có dạng \(\left( \beta \right)\): x – by + cz + d = 0. Khi đó S = 3b – c + d bằng bao nhiêu?
Đáp án:
Đáp án:
Áp dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng.
\(\left( \beta \right)\) // \(\left( \alpha \right)\) nên phương trình của \(\left( \beta \right)\) có dạng: x – 2y + 2z + d = 0 \((d \ne 2)\).
Theo đề bài: \(d\left( {M,(\beta )} \right) = 1 \Leftrightarrow \frac{{\left| {1 - 2.2 + 2.( - 1) + d} \right|}}{{\sqrt {{1^2} + {{( - 2)}^2} + {2^2}} }} = 1 \Leftrightarrow \left| {d - 5} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}d = 8\\d = 2\end{array} \right.\) .
Vì \(d \ne 2\) nên d = 8 thỏa mãn.
Suy ra \(\left( \beta \right)\): x – 2y + 2z + 8 = 0.
Vậy S = 3.2 – 2 + 8 = 12.
Gọi m, n là hai giá trị thực thỏa mãn giao tuyến của hai mặt phẳng \(({P_m})\): mx + 2y + nz + 1 = 0 và \(({Q_m})\): x – my + nz + 2 = 0 vuông góc với mặt phẳng \((\alpha )\): 4x – y – 6z + 3 = 0. Tính m + n.
Đáp án:
Đáp án:
Vì giao tuyến của \(({P_m})\) và \(({Q_m})\) vuông góc với \((\alpha )\) nên hai mặt phẳng đó cũng vuông góc với \((\alpha )\).
Áp dụng biểu thức tích vô hướng cho các vecto vuông góc để tính m, n.
Gọi vecto pháp tuyến của các mặt phẳng \(({P_m})\), \(({Q_m})\) và \((\alpha )\) lần lượt là \(\overrightarrow {{n_P}} \), \(\overrightarrow {{n_Q}} \) và \(\overrightarrow {{n_\alpha }} \). Ta có:
\(\overrightarrow {{n_P}} = (m;2;n)\), \(\overrightarrow {{n_Q}} = (1; - m;n)\), \(\overrightarrow {{n_\alpha }} = (4; - 1; - 6)\)
Vì giao tuyến của \(({P_m})\) và \(({Q_m})\) vuông góc với \((\alpha )\) nên hai mặt phẳng đó cũng vuông góc với \((\alpha )\).
Khi đó \(\left\{ \begin{array}{l}\overrightarrow {{n_\alpha }} .\overrightarrow {{n_P}} = 0\\\overrightarrow {{n_\alpha }} .\overrightarrow {{n_Q}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4m + 2.9 - 1) + n( - 6) = 0\\4 + ( - 1).( - m) + ( - 6).n = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4m - 6n = 2\\m - 6n = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2\\n = 1\end{array} \right. \Rightarrow m + n = 3\).
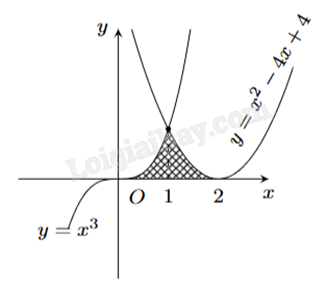
Áp dụng công thức tính diện tích của hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
Chia hình phẳng tô màu thành hai phần.
- Phần giới hạn bởi đồ thị \(y = {x^3}\), trục hoành, đường thẳng x = 0 và x = 1.
- Phần giới hạn bởi đồ thị \(y = {x^2} - 4x + 4\), trục hoành, đường thẳng x = 1 và x = 2.
\(S = \int\limits_0^1 {\left| {{x^3}} \right|dx} + \int\limits_1^2 {\left| {{x^2} - 4x + 4} \right|dx} = \int\limits_0^1 {{x^3}dx} + \int\limits_1^2 {\left( {{x^2} - 4x + 4} \right)dx} = \frac{7}{{12}} \approx 0,58\).
Tìm vecto pháp tuyến của (Q) bằng cách tính tích có hướng của \(\overrightarrow {AB} \) và vecto pháp tuyến của (P).
(Q) nhận \(\overrightarrow {AB} = (3 - 1;4 - 2; - 2 - 0) = (2;2; - 2)\) và \(\overrightarrow {{n_P}} = (1; - 1;1)\) làm cặp vecto chỉ phương.
Vecto pháp tuyến của (Q) là \(\overrightarrow {{n_Q}} = \left[ {\overrightarrow {AB} ,\overrightarrow {{n_P}} } \right] = (0; - 2; - 2)\).
Phương trình tổng quát của (Q) là:
\(0(x - 1) - 2(y - 2) - 2(z - 0) = 0 \Leftrightarrow - 2y - 2z + 4 = 0 \Leftrightarrow - y - z + 2 = 0\).
Vậy a + b + c = 0 + (-1) + (-1) = -2.
Từ hàm a(t), tìm v(t) và s(t) dựa vào nguyên hàm.
Tìm \({t_0}\) để \(v({t_0})\) lớn nhất và tính \(s({t_0})\).
\(v(t) = \int {a(t)dt} = \int {\left( {6 - 2t} \right)dt} = 6t - {t^2} + C\).
Vì ở thời điểm t = 0 thì ô tô dang dừng nên ta có \(v(0) = 0 \Leftrightarrow 6.0 - {0^2} + C = 0 \Leftrightarrow C = 0\).
Suy ra \(v(t) = 6t - {t^2}\).
\(s(t) = \int {v(t)dt} = \int {\left( {6t - {t^2}} \right)dt} = 3{t^2} - \frac{{{t^3}}}{3} + C'\).
Vì ở thời điểm t = 0 thì ô tô dang dừng nên ta có \(s(0) = 0 \Leftrightarrow {3.0^2} - \frac{{{0^3}}}{3} + C' = 0 \Leftrightarrow C' = 0\).
Suy ra \(s(t) = 3{t^2} - \frac{{{t^3}}}{3}\).
Xét hàm \(v(t) = 6t - {t^2}\), ta có \(v'(t) = a(t) = 6 - 2t = 0 \Leftrightarrow t = 3\).
Bảng biến thiên:
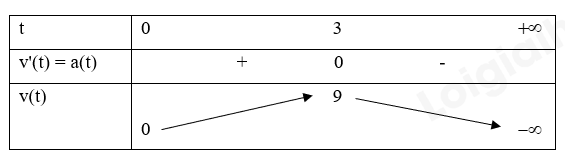
Từ bảng biến thiên suy ra vận tốc ô tô lớn nhất khi t = 3.
Khi đó, quãng đường ô tô chuyển động được là \(s(3) = {3.3^2} - \frac{{{3^3}}}{3} = 18\) (m).
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
