-
Đề thi giữa kì 1
- Đề thi giữa kì 1 - Đề số 1
- Đề thi giữa kì 1 - Đề số 2
- Đề thi giữa kì 1 - Đề số 3
- Đề thi giữa kì 1 - Đề số 4
- Đề thi giữa kì 1 - Đề số 5
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 7
- Đề thi giữa kì 1 - Đề số 8
- Đề thi giữa kì 1 - Đề số 9
- Đề thi giữa kì 1 - Đề số 10
- Đề thi giữa kì 1 - Đề số 11
- Đề thi giữa kì 1 - Đề số 12
- Đề thi giữa kì 1 - Đề số 13
-
Đề thi học kì 1
- Đề cương ôn tập học kì 1
- Đề thi học kì 1 - Đề số 1
- Đề thi học kì 1 - Đề số 2
- Đề thi học kì 1 - Đề số 3
- Đề thi học kì 1 - Đề số 4
- Đề thi học kì 1 - Đề số 5
- Đề thi học kì 1 - Đề số 6
- Đề thi học kì 1 - Đề số 7
- Đề thi học kì 1 - Đề số 8
- Đề thi học kì 1 - Đề số 9
- Đề thi học kì 1 - Đề số 10
- Đề thi học kì 1 - Đề số 11
- Đề thi học kì 1 - Đề số 12
- Đề thi học kì 1 - Đề số 13
- Đề thi học kì 1 - Đề số 14
- Đề thi học kì 1 - Đề số 15
- Đề thi học kì 1 - Đề số 16
- Đề thi học kì 1 - Đề số 17
- Đề thi học kì 1 - Đề số 18
-
Đề thi giữa kì 2
-
Đề thi học kì 2
- Đề cương ôn tập học kì 2
- Đề thi học kì 2 - Đề số 1
- Đề thi học kì 2 - Đề số 2
- Đề thi học kì 2 - Đề số 3
- Đề thi học kì 2 - Đề số 4
- Đề thi học kì 2 - Đề số 5
- Đề thi học kì 2 - Đề số 6
- Đề thi học kì 2 - Đề số 7
- Đề thi học kì 2 - Đề số 8
- Đề thi học kì 2 - Đề số 9
- Đề thi học kì 2 - Đề số 10
- Đề thi học kì 2 - Đề số 11
- Đề thi học kì 2 - Đề số 12
- Đề thi học kì 2 - Đề số 13
Đề thi học kì 1 Toán 7 Cánh diều - Đề số 16
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Số nào sau đây viết được dưới dạng số thập phân hữu hạn?
-
A.
\(1\frac{2}{7}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{2}{3}\).
-
D.
\(\sqrt 5 \).
Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi \(x = 5\) thì \(y = 2\). Hệ số tỉ lệ là:
-
A.
10.
-
B.
2,5.
-
C.
20.
-
D.
7.
\(\sqrt {25} \) có kết quả là
-
A.
-5 và 5.
-
B.
-5.
-
C.
5.
-
D.
25.
Giá trị của \(x\) trong tỉ lệ thức \(\frac{2}{5} = \frac{8}{x}\) là:
-
A.
1,25.
-
B.
4.
-
C.
40.
-
D.
20.
Làm tròn số thập phân 5897,9391 đến hàng phần mười được kết quả là:
-
A.
5898.
-
B.
5897,94.
-
C.
5897,9.
-
D.
5897,939.
Giá trị của biểu thức \(\sqrt {0,25} - \left| { - 0,2} \right|\) là:
-
A.
0,05.
-
B.
0,7.
-
C.
0,3.
-
D.
0,45.
Cho đẳng thức 4.9 = 3.12. Tỉ lệ thức nào sau đây không đúng?
-
A.
\(\frac{4}{9} = \frac{3}{{12}}\).
-
B.
\(\frac{4}{{12}} = \frac{3}{9}\).
-
C.
\(\frac{9}{{12}} = \frac{3}{4}\).
-
D.
\(\frac{9}{3} = \frac{{12}}{4}\).
Nếu \(\frac{x}{3} = \frac{y}{4}\) và \(x + y = 21\) thì
-
A.
\(x = 12;y = 9\).
-
B.
\(x = 63;y = 84\).
-
C.
\(x = - 9;y = - 12\).
-
D.
\(x = 9;y = 12\).
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {yOz} = 55^\circ \). Số đo của \(\widehat {xOy}\) là:
-
A.
\(115^\circ \).
-
B.
\(125^\circ \).
-
C.
\(55^\circ \).
-
D.
\(180^\circ \).
Khẳng định nào dưới đây đúng?
-
A.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 4 đường chéo.
-
B.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 4 đường chéo.
-
C.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 6 đường chéo.
-
D.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 6 đường chéo.
Cho Ot là tia phân giác của \(\widehat {xOy} = 120^\circ \). Chọn đáp án đúng:
-
A.
\(\widehat {xOy} = 60^\circ \).
-
B.
\(\widehat {xOt} = 120^\circ \).
-
C.
\(\widehat {yOt} = 120^\circ \).
-
D.
\(\widehat {xOt} = 60^\circ \).
-
A.
\(122^\circ \).
-
B.
\(132^\circ \).
-
C.
\(90^\circ \).
-
D.
\(58^\circ \).
Lời giải và đáp án
Số nào sau đây viết được dưới dạng số thập phân hữu hạn?
-
A.
\(1\frac{2}{7}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{2}{3}\).
-
D.
\(\sqrt 5 \).
Đáp án : B
Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.
\(\frac{1}{4}\) có thể viết dưới dạng số thập phân hữu hạn.
\(1\frac{2}{7}\); \(\frac{2}{3}\); \(\sqrt 5 \) không viết được dưới dạng số thập phân hữu hạn.
Đáp án B
Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi \(x = 5\) thì \(y = 2\). Hệ số tỉ lệ là:
-
A.
10.
-
B.
2,5.
-
C.
20.
-
D.
7.
Đáp án : A
Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \frac{a}{x}\) hay \(xy = a\) (với a là hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Hệ số tỉ lệ của x và y là: 5.2 = 10.
Đáp án A
\(\sqrt {25} \) có kết quả là
-
A.
-5 và 5.
-
B.
-5.
-
C.
5.
-
D.
25.
Đáp án : C
\(\sqrt a = x\) với \(x \ge 0,a = {x^2}\)
\(\sqrt {25} = 5\).
Đáp án C
Giá trị của \(x\) trong tỉ lệ thức \(\frac{2}{5} = \frac{8}{x}\) là:
-
A.
1,25.
-
B.
4.
-
C.
40.
-
D.
20.
Đáp án : D
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).
Ta có: \(\frac{2}{5} = \frac{8}{x}\) nên \(2x = 5.8 = 40\) suy ra \(x = \frac{{40}}{2} = 20\).
Đáp án D
Làm tròn số thập phân 5897,9391 đến hàng phần mười được kết quả là:
-
A.
5898.
-
B.
5897,94.
-
C.
5897,9.
-
D.
5897,939.
Đáp án : C
Áp dụng quy tắc Làm tròn số thập phân dương:
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5.
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên.
Số thập phân 5897,9391 làm tròn đến hàng phần mười là: 5897,9 (vì 3 < 5).
Đáp án C
Giá trị của biểu thức \(\sqrt {0,25} - \left| { - 0,2} \right|\) là:
-
A.
0,05.
-
B.
0,7.
-
C.
0,3.
-
D.
0,45.
Đáp án : C
Sử dụng kiến thức về căn bậc hai và giá trị tuyệt đối của một số:
\(\sqrt a = x\) nếu \(x \ge 0,a = {x^2}\);
|a| = a nếu a \( \ge \) 0;
|a| = -a nếu a < 0.
\(\sqrt {0,25} - \left| { - 0,2} \right| = 0,5 - 0,2 = 0,3\).
Đáp án C
Cho đẳng thức 4.9 = 3.12. Tỉ lệ thức nào sau đây không đúng?
-
A.
\(\frac{4}{9} = \frac{3}{{12}}\).
-
B.
\(\frac{4}{{12}} = \frac{3}{9}\).
-
C.
\(\frac{9}{{12}} = \frac{3}{4}\).
-
D.
\(\frac{9}{3} = \frac{{12}}{4}\).
Đáp án : A
Nếu a.d = b.c thì \(\frac{a}{c} = \frac{b}{d};\frac{a}{b} = \frac{c}{d};\frac{c}{a} = \frac{d}{b};\frac{b}{a} = \frac{d}{c}\)
Nếu 4.9 = 3.12 thì \(\frac{4}{3} = \frac{{12}}{9};\frac{4}{{12}} = \frac{3}{9};\frac{3}{4} = \frac{9}{{12}};\frac{{12}}{4} = \frac{9}{3}\) nên A sai.
Đáp án A
Nếu \(\frac{x}{3} = \frac{y}{4}\) và \(x + y = 21\) thì
-
A.
\(x = 12;y = 9\).
-
B.
\(x = 63;y = 84\).
-
C.
\(x = - 9;y = - 12\).
-
D.
\(x = 9;y = 12\).
Đáp án : D
Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{a}{c} = \frac{b}{d} = \frac{{a + b}}{{c + d}}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3} = \frac{y}{4} = \frac{{x + y}}{{3 + 4}} = \frac{{21}}{7} = 3\)
suy ra \(x = 3.3 = 9;y = 3.4 = 12\).
Đáp án D
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {yOz} = 55^\circ \). Số đo của \(\widehat {xOy}\) là:
-
A.
\(115^\circ \).
-
B.
\(125^\circ \).
-
C.
\(55^\circ \).
-
D.
\(180^\circ \).
Đáp án : B
Hai góc kề bù thì có tổng bằng \(180^\circ \).
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \)
suy ra \(\widehat {xOy} = 180^\circ - \widehat {yOz} = 180^\circ - 55^\circ = 125^\circ \).
Đáp án B
Khẳng định nào dưới đây đúng?
-
A.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 4 đường chéo.
-
B.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 4 đường chéo.
-
C.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 6 đường chéo.
-
D.
Hình hộp chữ nhật có 12 đỉnh, 8 cạnh và 6 đường chéo.
Đáp án : A
Dựa vào đặc điểm của hình hộp chữ nhật.
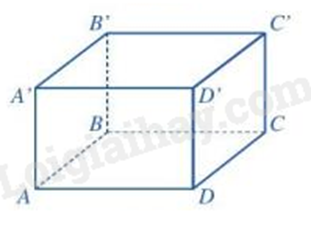
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh và 4 đường chéo nên đáp án A đúng.
Đáp án A
Cho Ot là tia phân giác của \(\widehat {xOy} = 120^\circ \). Chọn đáp án đúng:
-
A.
\(\widehat {xOy} = 60^\circ \).
-
B.
\(\widehat {xOt} = 120^\circ \).
-
C.
\(\widehat {yOt} = 120^\circ \).
-
D.
\(\widehat {xOt} = 60^\circ \).
Đáp án : D
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Vì Ot là tia phân giác của \(\widehat {xOy} = 120^\circ \) nên \(\widehat {xOt} = \widehat {yOt} = \frac{{120^\circ }}{2} = 60^\circ \).
Đáp án D
-
A.
\(122^\circ \).
-
B.
\(132^\circ \).
-
C.
\(90^\circ \).
-
D.
\(58^\circ \).
Đáp án : D
Hai đường thẳng song song thì có các góc so le trong bằng nhau, các góc đồng vị bằng nhau.
Vì a // b nên \(\widehat {{B_3}} = \widehat {{A_1}} = 58^\circ \) (hai góc so le trong)
Đáp án D
Áp dụng quy tắc cộng, trừ, nhân, chia với số hữu tỉ.
b) Sử dụng tính chất chia hai lũy thừa có cùng cơ số.
c) Thực hiện phép tính trong ngoặc sau đó tính lũy thừa và rút gọn.
a) \(\frac{1}{2} + \frac{2}{3} - \frac{4}{5}\)\( = \frac{{15 + 20 - 24}}{{30}} = \frac{{11}}{{30}}\)
b) \(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^9}:{\left( {\frac{1}{3}} \right)^7} - 2\)\(\frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^{9 - 7}} - 2\)\( = \frac{{17}}{9} + {\left( {\frac{1}{3}} \right)^2} - 2\)\( = \frac{{17}}{9} + \frac{1}{9} - 2\)\( = 2 - 2\)\( = 0\)
c) \(\left( {1 + \frac{1}{2} + \frac{1}{3}} \right){\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\)\( = \left( {\frac{{6 + 3 + 2}}{6}} \right){\left( {\frac{{16 - 15}}{{20}}} \right)^2}\)\( = \frac{{11}}{6}.{\left( {\frac{1}{{20}}} \right)^2}\)\( = \frac{{11}}{6}.\frac{1}{{400}}\)\( = \frac{{11}}{{2400}}\)
Áp dụng quy tắc chuyển vế đổi dấu.
b) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B.
a) \(\frac{2}{5}x - \frac{1}{2} = \frac{{ - 3}}{5}\)
\(\begin{array}{l}\frac{2}{5}x = \frac{{ - 3}}{5} + \frac{1}{2}\\\frac{2}{5}x = \frac{{ - 1}}{{10}}\\x = \frac{{ - 1}}{{10}}:\frac{2}{5}\\x = \frac{{ - 1}}{4}\end{array}\)
Vậy \(x = \frac{{ - 1}}{4}\).
b) \(\left| {x - \frac{1}{2}} \right| = \frac{2}{3}\)
\(x - \frac{1}{2} = \frac{2}{3}\) hoặc \(x - \frac{1}{2} = - \frac{2}{3}\)
\(x = \frac{2}{3} + \frac{1}{2}\) hoặc \(x = - \frac{2}{3} + \frac{1}{2}\)
\(x = \frac{7}{6}\) hoặc \(x = \frac{{ - 1}}{6}\)
Vậy \(x \in \left\{ {\frac{7}{6};\frac{{ - 1}}{6}} \right\}\)
Gọi số chiếc bút bi đỏ, đen và xanh lần lượt là: x, y, z (chiếc), \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)
Lập luận \(x + y + z = 340\)
Lập luận \(\frac{x}{4} = \frac{y}{6} = \frac{z}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.
Gọi số chiếc bút bi đỏ, đen và xanh lần lượt là: x, y, z (chiếc), \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)
Vì cửa hàng nhập về bán 340 chiếc nên \(x + y + z = 340\).
Vì số chiếc bút bi đỏ, đen và xanh tỉ lệ với các số 4; 6; 7 nên ta có: \(\frac{x}{4} = \frac{y}{6} = \frac{z}{7}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{4} = \frac{y}{6} = \frac{z}{7} = \frac{{x + y + z}}{{4 + 6 + 7}} = \frac{{340}}{{17}} = 20\)
suy ra \(x = 20.4 = 80\); \(y = 20.6 = 120\); \(z = 20.7 = 140\).
Vậy số chiếc bút bi đỏ, đen và xanh lần lượt là 80 chiếc; 120 chiếc; 140 chiếc.
Áp dụng công thức tính diện tích xung quanh của hình hộp chữ nhật để tính diện tích cần sơn chiếc thùng:
Sxq = Cđáy.chiều cao.
Số ki-lô-gam sơn = Sxq : 4.
Diện tích cần sơn là: \(2.\left( {2 + 1,5} \right).1,2 = 8,4\left( {{m^2}} \right)\)
Số ki-lô-gam sơn cần dùng là: \(8,4:4 = 2,1\left( {kg} \right)\)
Vậy người thợ cần 2,1kg sơn để sơn bên ngoài các mặt xung quanh chiếc thùng đó.
a) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau.
b) Áp dụng tính chất hai góc kề bù có tổng bằng \(180^\circ \) và hai đường thẳng song song thì hai góc so le trong bằng nhau.
c) Chứng minh hai góc ở vị trí đồng vị bằng nhau nên Dx // Cy.
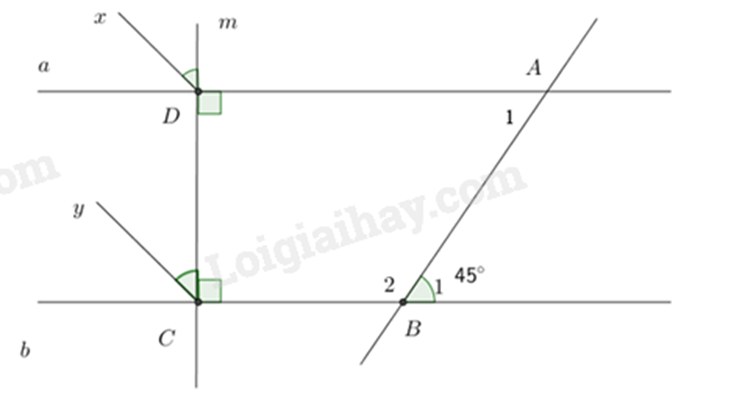
a) Ta có: \(a \bot m\) (gt), \(b \bot m\) (gt) nên a // b.
b) Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù)
\(45^\circ + \widehat {{B_2}} = 180^\circ \) suy ra \(\widehat {{B_2}} = 180^\circ - 45^\circ = 135^\circ \).
Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (hai góc so le trong)
Mà \(\widehat {{B_1}} = 45^\circ \) nên \(\widehat {{A_1}} = 45^\circ \).
c) Vì Dx là tia phân giác của \(\widehat {aDm}\) (gt) nên \(\widehat {xDm} = 90^\circ :2 = 45^\circ \)
Vì \(Cy\) là tia phân giác của \(\widehat {bCD}\) (gt) nên \(\widehat {yCD} = 90^\circ :2 = 45^\circ \)
Do đó \(\widehat {xDm} = \widehat {yCD}\)
Mà hai góc này ở vị trí đồng vị nên Dx // Cy.
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm)
Phần trắc nghiệm (3 điểm)
Phần trắc nghiệm (3 điểm)
Phần trắc nghiệm (3 điểm)
Phần trắc nghiệm (3 điểm)
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
A. NỘI DUNG ÔN TẬP Đại số
>> Học trực tuyến lớp 7 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
