Đề thi học kì 1 Toán 12 - Đề số 6
Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề thi học kì 1 Toán 12 - Đề số 6
Đề bài
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ.
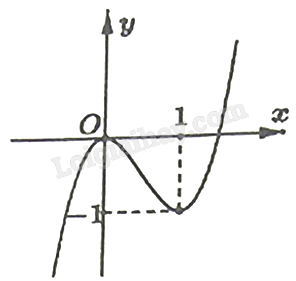
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\((-\infty;0)\).
-
B.
\((1;+\infty)\).
-
C.
\((-\infty;+\infty)\).
-
D.
\((0;1)\).
-
A.
$x = - 2$.
-
B.
$x = 1$.
-
C.
$x = - 1$.
-
D.
$x = 2$.
Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-2;4] bằng
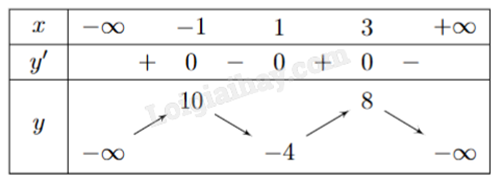
-
A.
-1
-
B.
10
-
C.
1
-
D.
8
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{3x - 7}}{{x + 2}}\) là:
-
A.
(3;-2)
-
B.
(-2;3)
-
C.
(2;-3)
-
D.
(-3;2)
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f’(x) như hình vẽ dưới đây.

Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
-
A.
\((2;3)\)
-
B.
\(( - 10; - 5)\)
-
C.
\((0;1)\)
-
D.
\((0;2)\)
Cho hình lập phương ABCD.A’B’C’D' (tham khảo hình vẽ).
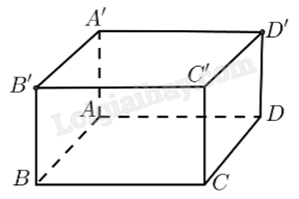
Góc giữa hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD'} \) bằng
-
A.
\({135^o}\)
-
B.
\({60^o}\)
-
C.
\({30^o}\)
-
D.
\({45^o}\)
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(3;5;2) trên mặt phẳng (Oxy) có tọa độ là
-
A.
(5;3;0)
-
B.
(3;5;0)
-
C.
(0;5;2)
-
D.
(3;0;2)
Không gian với trục hệ tọa độ \(Oxyz\), cho \(\overrightarrow a = 2\overrightarrow j - \overrightarrow i + 3\overrightarrow k .\) Tọa độ của vectơ \(\overrightarrow a \) là
-
A.
\(\overrightarrow a \left( { - 1;2; - 3} \right)\)
-
B.
\(\overrightarrow a \left( {2; - 1;3} \right)\)
-
C.
\(\overrightarrow a \left( { - 1;2;3} \right)\)
-
D.
\(\overrightarrow a \left( {2; - 1; - 3} \right)\)
Trong không gian Oxy, cho hai điểm A(-2;1;0), B(3;-2;1). Tọa độ của vecto \(\overrightarrow {AB} \) là
-
A.
\(( - 5;3; - 1)\)
-
B.
\((5; - 3;1)\)
-
C.
\((1; - 1;1)\)
-
D.
\(( - 1;1; - 1)\)
Trong không gian Oxyz, cho hai điểm A(1; 2; -1) và B(2; 4; 1). Trọng tâm của tam giác OAB có tọa độ là
-
A.
(1; 2; 0).
-
B.
(-1; -2; 0).
-
C.
(3; 6; 0).
-
D.
(1; 3; 0).
Bảng thống kê dưới đây cho biết thu nhập bình quân đầu người/tháng của người dân Hà Nội (tính theo triệu đồng) trong giai đoạn từ năm 2018 đến năm 2024:

Mẫu số liệu thống kê trên có khoảng biến thiên bằng bao nhiêu (tính theo triệu đồng)?
-
A.
2,660
-
B.
1,645
-
C.
0,867
-
D.
2,290
Một bệnh viện thống kê lại số cân nặng của 20 bé sơ sinh trong bảng sau:

Phương sai của mẫu số liệu ghép nhóm là
-
A.
3,39
-
B.
11,62
-
C.
0,1314
-
D.
0,36
Trong không gian với hệ toạ độ $Oxyz$, cho ba vectơ $\vec{a} = (-2; 1; 1)$, $\vec{b} = (2; -1; 1)$, $\vec{c} = (x; 1; y)$. Xét tính đúng sai các mệnh đề sau:
a) $|\vec{a}| = \sqrt{6}$.
b) Tọa độ của $\vec{u} = -2\vec{a} + 3\vec{b}$ là $(10; -5; 4)$.
c) Vectơ $\vec{c}$ cùng phương với vectơ $\vec{b}$ thì $x + y = 3$.
d) Gọi $\varphi$ là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$. Khi đó $\cos \varphi = -\frac{2}{3}$.
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:
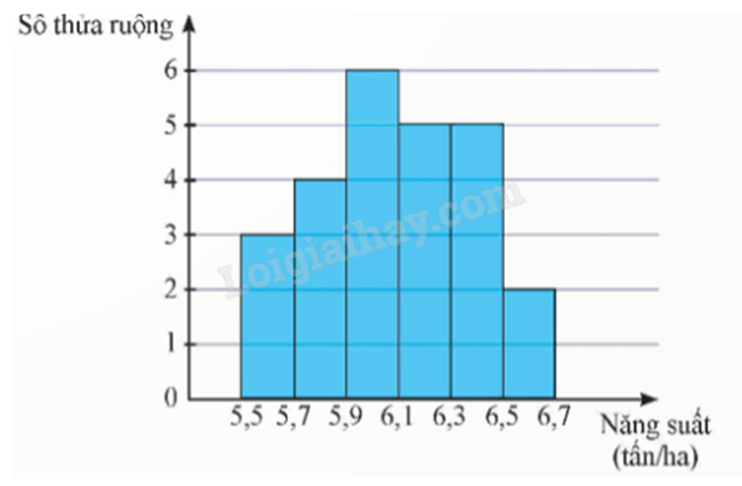
a) Có 25 thửa ruộng đã được khảo sát.
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 6,33.
d) Phương sai của mẫu số liệu ghép nhóm trên là 0,086656.
Cho hàm số $y = ax^3 + bx^2 + cx + d$ có đồ thị như sau:

Tính giá trị biểu thức T = a + 2b + 3c + 4d.
Một doanh nghiệp dự định sản xuất 200 máy tính bảng dành cho học sinh. Nếu doanh nghiệp đó bán x máy tính bảng \(\left( {1 \le x \le 200,x \in \mathbb{N}} \right)\) thì giá bán cho mỗi máy tính bảng là \(p(x) = 4000 - 10x\) (nghìn đồng), trong đó chi phí để sản xuất mỗi máy tính bảng là \(c(x) = {x^2} - 70x + 400 + \frac{{1000}}{x}\) (nghìn đồng). Hỏi doanh nghiệp đó sẽ bán bao nhiêu máy tính bảng để lợi nhuận cao nhất?
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho các lực căng $\overrightarrow{F_1}, \overrightarrow{F_2}, \overrightarrow{F_3}$ lần lượt trên mỗi dây OA, OB, OC đều có độ lớn bằng 60 (N). Cho biết các đường thẳng OA, OB, OC cùng tạo với mặt phẳng ngang một góc bằng $30^o$. Tính trọng lượng của chiếc đèn tròn đó.

Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8 m, chiều rộng là 6 m và chiều cao là 3 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét. Khi đó, tọa độ của điểm treo đèn là I(x; y; z), hãy tính x + y + z.
Lời giải và đáp án
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ.

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\((-\infty;0)\).
-
B.
\((1;+\infty)\).
-
C.
\((-\infty;+\infty)\).
-
D.
\((0;1)\).
Đáp án : D
Dựa vào đồ thị hàm số, chỉ ra sự biến thiên.
Hàm số đã cho nghịch biến trên \((0;1)\).
-
A.
$x = - 2$.
-
B.
$x = 1$.
-
C.
$x = - 1$.
-
D.
$x = 2$.
Đáp án : C
Quan sát bảng biến thiên và nhận xét.
Hàm số đạt cực đại tại $x = - 1$.
Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-2;4] bằng

-
A.
-1
-
B.
10
-
C.
1
-
D.
8
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Quan sát bảng biến thiên, ta thấy giá trị lớn nhất của f(x) trên [-2;4] là f(-1) = 10.
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{3x - 7}}{{x + 2}}\) là:
-
A.
(3;-2)
-
B.
(-2;3)
-
C.
(2;-3)
-
D.
(-3;2)
Đáp án : B
Tâm đối xứng của đồ thị là giao điểm của các đường tiệm cận.
Đồ thị hàm số có tiệm cận đứng x = -2 và tiệm cận ngang y = 3, suy ra tâm đối xứng là giao điểm của hai tiệm cận có tọa độ (-2;3).
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f’(x) như hình vẽ dưới đây.

Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
-
A.
\((2;3)\)
-
B.
\(( - 10; - 5)\)
-
C.
\((0;1)\)
-
D.
\((0;2)\)
Đáp án : A
Quan sát bảng xét dấu và nhận xét.
Hàm số y = f(x) đồng biến trên khoảng (2;3) vì trên khoảng đó, f’(x) > 0.
Cho hình lập phương ABCD.A’B’C’D' (tham khảo hình vẽ).

Góc giữa hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD'} \) bằng
-
A.
\({135^o}\)
-
B.
\({60^o}\)
-
C.
\({30^o}\)
-
D.
\({45^o}\)
Đáp án : A
Nếu a // b thì (a,c) = (b,c).
\(\left( {\overrightarrow {AB} ,\overrightarrow {CD'} } \right) = \left( {\overrightarrow {DC} ,\overrightarrow {CD'} } \right) = {180^o} - \left( {\overrightarrow {CD} ,\overrightarrow {CD'} } \right) = {180^o} - {45^o} = {135^o}\).
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(3;5;2) trên mặt phẳng (Oxy) có tọa độ là
-
A.
(5;3;0)
-
B.
(3;5;0)
-
C.
(0;5;2)
-
D.
(3;0;2)
Đáp án : B
Hình chiếu vuông góc của điểm (x;y;z) trên mặt phẳng (Oxy) có tọa độ là (x;y;0).
Hình chiếu vuông góc của điểm (3;5;2) trên mặt phẳng (Oxy) có tọa độ là (3;5;0).
Không gian với trục hệ tọa độ \(Oxyz\), cho \(\overrightarrow a = 2\overrightarrow j - \overrightarrow i + 3\overrightarrow k .\) Tọa độ của vectơ \(\overrightarrow a \) là
-
A.
\(\overrightarrow a \left( { - 1;2; - 3} \right)\)
-
B.
\(\overrightarrow a \left( {2; - 1;3} \right)\)
-
C.
\(\overrightarrow a \left( { - 1;2;3} \right)\)
-
D.
\(\overrightarrow a \left( {2; - 1; - 3} \right)\)
Đáp án : C
\(\overrightarrow a = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = \left( {m;n;p} \right)\).
\(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j + 3\overrightarrow k = \left( { - 1;2;3} \right)\).
Trong không gian Oxy, cho hai điểm A(-2;1;0), B(3;-2;1). Tọa độ của vecto \(\overrightarrow {AB} \) là
-
A.
\(( - 5;3; - 1)\)
-
B.
\((5; - 3;1)\)
-
C.
\((1; - 1;1)\)
-
D.
\(( - 1;1; - 1)\)
Đáp án : B
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\).
\(\overrightarrow {AB} = (3 + 2; - 2 - 1;1 - 0) = (5; - 3;1)\).
Trong không gian Oxyz, cho hai điểm A(1; 2; -1) và B(2; 4; 1). Trọng tâm của tam giác OAB có tọa độ là
-
A.
(1; 2; 0).
-
B.
(-1; -2; 0).
-
C.
(3; 6; 0).
-
D.
(1; 3; 0).
Đáp án : A
Trong không gian với hệ trục toạ độ Oxyz, cho điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\), \(B\left( {{x_B};{y_B};{z_B}} \right)\), \(C\left( {{x_C};{y_C};{z_C}} \right)\).
Toạ độ trọng tâm G của tam giác ABC là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\).
Trọng tâm tam giác là \(G\left( {\frac{{0 + 1 + 2}}{3};\frac{{0 + 2 + 4}}{3};\frac{{0 - 1 + 1}}{3}} \right) \Rightarrow G(1;2;0)\).
Bảng thống kê dưới đây cho biết thu nhập bình quân đầu người/tháng của người dân Hà Nội (tính theo triệu đồng) trong giai đoạn từ năm 2018 đến năm 2024:

Mẫu số liệu thống kê trên có khoảng biến thiên bằng bao nhiêu (tính theo triệu đồng)?
-
A.
2,660
-
B.
1,645
-
C.
0,867
-
D.
2,290
Đáp án : B
Lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên (chứa mẫu số liệu).
Khoảng biến thiên của mẫu số liệu là \(R = 7,546 - 5,901 = 1,645\).
Một bệnh viện thống kê lại số cân nặng của 20 bé sơ sinh trong bảng sau:

Phương sai của mẫu số liệu ghép nhóm là
-
A.
3,39
-
B.
11,62
-
C.
0,1314
-
D.
0,36
Đáp án : C
Lập bảng tần số theo giá trị đại diện, tính số trung bình rồi tính phương sai.

Số trung bình: \(\overline {\rm{x}} = \frac{{3.2,85 + 6.3,15 + 5.3,45 + 4.3,75 + 2.4,05}}{{20}} = 3,39\).
Phương sai: \({s^2} = \frac{{3.2,{{85}^2} + 6.3,{{15}^2} + 5.3,{{45}^2} + 4.3,{{75}^2} + 2.4,{{05}^2}}}{{20}} - 3,{39^2} = 0,1314\).
Trong không gian với hệ toạ độ $Oxyz$, cho ba vectơ $\vec{a} = (-2; 1; 1)$, $\vec{b} = (2; -1; 1)$, $\vec{c} = (x; 1; y)$. Xét tính đúng sai các mệnh đề sau:
a) $|\vec{a}| = \sqrt{6}$.
b) Tọa độ của $\vec{u} = -2\vec{a} + 3\vec{b}$ là $(10; -5; 4)$.
c) Vectơ $\vec{c}$ cùng phương với vectơ $\vec{b}$ thì $x + y = 3$.
d) Gọi $\varphi$ là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$. Khi đó $\cos \varphi = -\frac{2}{3}$.
a) $|\vec{a}| = \sqrt{6}$.
b) Tọa độ của $\vec{u} = -2\vec{a} + 3\vec{b}$ là $(10; -5; 4)$.
c) Vectơ $\vec{c}$ cùng phương với vectơ $\vec{b}$ thì $x + y = 3$.
d) Gọi $\varphi$ là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$. Khi đó $\cos \varphi = -\frac{2}{3}$.
a) \(\overrightarrow a = (x;y;z) \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{x^2} + {y^2} + {z^2}} \).
b) Cho \(\overrightarrow a ({x_a};{y_a};{z_a})\), \(\overrightarrow b ({x_b};{y_b};{z_b})\) và số thực k.
+ \(\overrightarrow a + \overrightarrow b = ({x_a} + {x_b};{y_a} + {y_b};{z_a} + {z_b})\).
+ \(\overrightarrow a - \overrightarrow b = ({x_a} - {x_b};{y_a} - {y_b};{z_a} - {z_b})\).
+ \(k\overrightarrow a = (k{x_a};k{y_a};k{z_a})\).
c) Nếu \(\overrightarrow a \) cùng phương với \(\overrightarrow b \) thì \(\overrightarrow a = k\overrightarrow b \).
d) \(\cos \alpha = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}}}{{\sqrt {{x_a}^2 + {y_a}^2 + {z_a}^2} .\sqrt {{x_b}^2 + {y_b}^2 + {z_b}^2} }}\).
a) Đúng. \(\left| {\overrightarrow a } \right| = \sqrt {{{( - 2)}^2} + {1^2} + {1^2}} = \sqrt 6 \).
b) Sai. \(\overrightarrow u = \left( { - 2.( - 2) + 3.2; - 2.1 + 3.( - 1); - 2.1 + 3.1} \right) = \left( {10; - 5;1} \right)\).
c) Sai. \(\overrightarrow c \) cùng phương với \(\overrightarrow b \) khi \(\overrightarrow c = k\overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}x = 2k\\1 = - k\\y = k\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}k = - 1\\x = - 2\\y = - 1\end{array} \right. \Rightarrow x + y = - 3\).
d) Đúng. \(\cos \varphi = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 2.2 + 1.( - 1) + 1.1}}{{\sqrt {{{( - 2)}^2} + {1^2} + {1^2}} .\sqrt {{2^2} + {{( - 1)}^2} + {1^2}} }} = - \frac{2}{3}\).
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:

a) Có 25 thửa ruộng đã được khảo sát.
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 6,33.
d) Phương sai của mẫu số liệu ghép nhóm trên là 0,086656.
a) Có 25 thửa ruộng đã được khảo sát.
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 6,33.
d) Phương sai của mẫu số liệu ghép nhóm trên là 0,086656.
Lập bảng tần số ghép nhóm từ biểu đồ. Áp dụng công thức tính khoảng biến thiên, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm.
a) Đúng. Số thửa ruộng được khảo sát là: n = 3 + 4 + 6 + 5 + 5 + 2 = 25.
b) Đúng. Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:
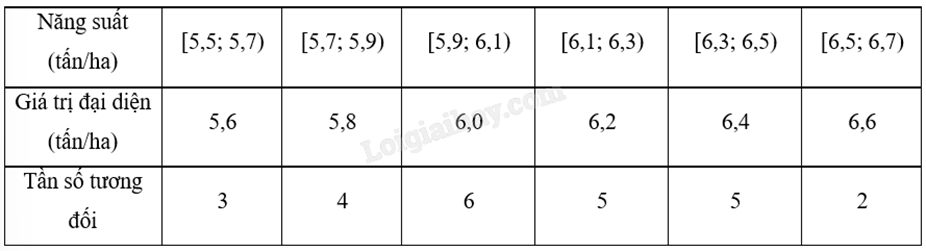
Khoảng biến thiên của mẫu số liệu đã cho là: R = 6,7 – 5,5 = 1,2 (tấn/ha).
c) Sai. Ta có:
Cỡ mẫu n = 25.
Gọi \({x_1};...;{x_{25}}\) là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{{{x_6} + {x_7}}}{2} \in \) [5,7; 5,9). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 5,7 + \frac{{\frac{{25}}{4} - 3}}{4}\left( {5,9 - 5,7} \right) = 5,8625\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{{{x_{19}} + {x_{20}}}}{2} \in \) [6,3; 6,5). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,3 + \frac{{\frac{{3.25}}{4} - \left( {3 + 4 + 6 + 5} \right)}}{5}\left( {6,5 - 6,3} \right) = 6,33\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 6,33 - 5,8625 = 0,4675\).
d) Đúng. Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{3.5,6 + 4.5,8 + 6.6,2 + 5.6,4 + 2.6,6}}{{25}} = 6,088\).
Phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{{25}}\left[ {3.{{\left( {5,6} \right)}^2} + 4.{{\left( {5,8} \right)}^2} + 6.{{\left( {6,0} \right)}^2} + 5.{{\left( {6,2} \right)}^2} + 5.{{\left( {6,4} \right)}^2} + 2.{{\left( {6,6} \right)}^2}} \right] - {\left( {6,088} \right)^2} = 0,086656\).
Cho hàm số $y = ax^3 + bx^2 + cx + d$ có đồ thị như sau:

Tính giá trị biểu thức T = a + 2b + 3c + 4d.
Tìm 4 điểm đồ thị đi qua, thay tọa độ vào hàm số, giải hệ tìm các hệ số a, b, c, d.
Do đồ thị đi qua 4 điểm (-1; 0), (0; 4), (1; 2), (2; 0) nên ta có hệ phương trình:
$\left. \left\{ \begin{array}{l} {- a + b - c + d = 0} \\ \begin{array}{l} {d = 4} \\ {a + b + c + d = 2} \\ {8a + 4b + 2c + d = 0} \end{array} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {a = 1} \\ {b = - 3} \\ {c = 0} \\ {d = 4} \end{array} \right. \right.$. Suy ra T = 11.
Một doanh nghiệp dự định sản xuất 200 máy tính bảng dành cho học sinh. Nếu doanh nghiệp đó bán x máy tính bảng \(\left( {1 \le x \le 200,x \in \mathbb{N}} \right)\) thì giá bán cho mỗi máy tính bảng là \(p(x) = 4000 - 10x\) (nghìn đồng), trong đó chi phí để sản xuất mỗi máy tính bảng là \(c(x) = {x^2} - 70x + 400 + \frac{{1000}}{x}\) (nghìn đồng). Hỏi doanh nghiệp đó sẽ bán bao nhiêu máy tính bảng để lợi nhuận cao nhất?
Lập hàm số biểu diễn lợi nhuận của doanh nghiệp theo x.
Tìm x sao cho hàm số đạt GTLN bằng cách sử dụng đạo hàm.
Lợi nhuận = Doanh thu – Chi phí.
Lợi nhuận khi bán x chiếc máy tính bảng là:
\(L(x) = x.p(x) - x.c(x)\)
\( = x.\left( {4000 - 10x} \right) - x.\left( {{x^2} - 70x + 400 + \frac{{1000}}{x}} \right)\)
\( = 4000x - 10{x^2} - {x^3} + 70{x^2} - 400x - 1000\)
\( = - {x^3} + 60{x^2} + 3600x - 1000\).
Ta có \(L'(x) = - 3{x^2} + 120x + 3600 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 60\\x = - 20\end{array} \right.\)
Xét trên đoạn [1;200], ta có:
L(1) = 2659; L(60) = 215000; L(200) = -4881000.
Vậy lợi nhuận lớn nhất khi doanh nghiệp bán 60 máy tính.
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho các lực căng $\overrightarrow{F_1}, \overrightarrow{F_2}, \overrightarrow{F_3}$ lần lượt trên mỗi dây OA, OB, OC đều có độ lớn bằng 60 (N). Cho biết các đường thẳng OA, OB, OC cùng tạo với mặt phẳng ngang một góc bằng $30^o$. Tính trọng lượng của chiếc đèn tròn đó.

Áp dụng tính chất trọng tâm của vecto và hệ thức lượng trong tam giác vuông để tính.
Theo giả thiết ta có O.ABC là hình chóp đều với OA = OB = OC = 60 và góc tạo bởi mỗi đường thẳng OA, OB, OC với (ABC) là $30^{o}$.
Gọi G là trọng tâm của tam giác ABC thì $OG\bot(ABC)$ và $\widehat{OAG} = \widehat{OBG} = \widehat{OCG} = 30^{o}$.
Gọi T là trọng lượng của đèn tròn thì $T = \left| {\overset{\rightarrow}{OA} + \overset{\rightarrow}{OB} + \overset{\rightarrow}{OC}} \right| = \left| {3\overset{\rightarrow}{OG}} \right| = 3OG$.
Trong tam giác OAG vuông tại G, ta có:
$OG = OA\sin\widehat{OAG} = 60\sin 30^{o} = 30$.
Vậy trọng lượng của đèn là T = 3.30 = 90 (N).
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8 m, chiều rộng là 6 m và chiều cao là 3 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét. Khi đó, tọa độ của điểm treo đèn là I(x; y; z), hãy tính x + y + z.
Áp dụng định nghĩa vecto bằng nhau.
Giả sử căn phòng hình hộp chữ nhật được mô phỏng như hình vẽ.

Khi đó ta có B'(6; 8; 3) và O'(0; 0; 3).
Gọi I(x; y; z) là điểm chính giữa trần nhà của phòng học.
Vì O'A'B'C' là hình chữ nhật nên $\overset{\rightarrow}{O^{\prime}I} = \overset{\rightarrow}{IB^{\prime}}$.
Ta có $\overset{\rightarrow}{O'I} = \left( {x - 0;y - 0;z - 3} \right)$), $\overset{\rightarrow}{IB'} = \left( {6 - x;8 - y;3 - z} \right)$ nên:
$\left. \overset{\rightarrow}{O^{\prime}I} = \overset{\rightarrow}{IB^{\prime}}\Leftrightarrow\left\{ \begin{array}{l} {x - 0 = 6 - x} \\ {y - 0 = 8 - y} \\ {z - 3 = 3 - z} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {x = 3} \\ {y = 4} \\ {z = 3} \end{array} \right. \right.$
Vậy tọa độ điểm treo đèn là I(3; 4; 3) $\Rightarrow$ x + y + z = 3 + 4 + 3 = 10.
a) Tìm tập xác định, xét dấu đạo hàm.
b) Tìm giá trị lớn nhất, nhỏ nhất của \(y = \frac{{{x^2}}}{{x + 1}}\) trên \(\left( { - 1;1} \right]\).
a) Tập xác định: \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có \(y' = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} \Rightarrow y' = 0 \Leftrightarrow \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} = 0 \Leftrightarrow x = - 2\) hoặc \(x = 0\).
Ta có bảng biến thiên:
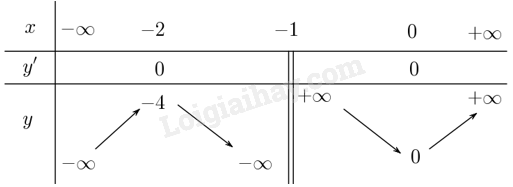
b) Đặt \(x = \cos \alpha \), ta có \(M = \frac{{{x^2}}}{{x + 1}},x \in \left( { - 1;1} \right]\).
Dựa vào bảng biến thiên ta có \(\min M = \mathop {\min }\limits_{\left( { - 1;1} \right]} \frac{{{x^2}}}{{x + 1}} = 0\) và \(\max M = \mathop {\max }\limits_{\left( { - 1;1} \right]} \frac{{{x^2}}}{{x + 1}} = y\left( 1 \right) = \frac{1}{2}\).
a) Sử dụng kiến thức về độ dài đoạn thẳng trong không gian để tính:
Nếu \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
b) Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính:
Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx' + yy' + zz'}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{'^2} + y{'^2} + z{'^2}} }}\).
a) Ta có: \(\overrightarrow {AB} \left( {3; - 4;0} \right) \Rightarrow AB = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5\);
\(\overrightarrow {AC} \left( { - 2;3;6} \right) \Rightarrow AC = \sqrt {{{\left( { - 2} \right)}^2} + {3^2} + {6^2}} = 7\).
\(\overrightarrow {BC} = ( - 5;7;6) \Rightarrow BC = \sqrt {{{( - 5)}^2} + {7^2} + {6^2}} = \sqrt {110} \).
Chu vi tam giác ABC là: \(5 + 7 + \sqrt {110} = 12 + \sqrt {110} \).
b) \(\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{3.\left( { - 2} \right) + \left( { - 4} \right).3 + 0.6}}{{5.7}} = \frac{{ - 18}}{{35}} \).
\(\Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) \approx 121^o\).
Vậy \(\widehat {BAC} = 121^o\).
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
a) Bảng tần số ghép nhóm:

b) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 100 - 60 = 40\) (g).
Gọi \({x_1};{x_2};...;{x_{80}}\) là mẫu số liệu gốc gồm cân nặng của 80 con tôm càng xanh 5 tháng tuổi theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right) \in \left[ {70;80} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 70 + \frac{{\frac{{1.80}}{4} - 10}}{{20}}\left( {80 - 70} \right) = 75\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{60}} + {x_{61}}} \right) \in \left[ {90;100} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 90 + \frac{{\frac{{3.80}}{4} - \left( {10 + 20 + 30} \right)}}{{20}}\left( {100 - 90} \right) = 90\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 90 - 75 = 15\) (g).
Đề thi học kì 1 Toán 12 - Đề số 7
Đề thi học kì 1 Toán 12 - Đề số 8
Đề thi học kì 1 Toán 12 - Đề số 9
Đề thi học kì 1 Toán 12 - Đề số 10
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số 1. Tính đơn điệu và cực trị của hàm số 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3. Đường tiệm cận của đồ thị hàm số 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn











Danh sách bình luận