Đề thi học kì 2 Toán 12 Kết nối tri thức - Đề số 1
Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Nguyên hàm của hàm số y = sinx + 2cosx là
-
A.
cosx – 2sinx + C
-
B.
-cosx + 2sinx + C
-
C.
cosx + 2sinx + C
-
D.
-cosx – 2sinx + C
Cho hàm số f(x) liên tục trên đoạn [a;b]. Hãy chọn mệnh đề sai dưới đây.
-
A.
\(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \)
-
B.
\(\int\limits_a^b {kdx} = k(b - a)\), \(\forall k \in \mathbb{R}\)
-
C.
\(\int\limits_a^b {f(x)dx} = \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} \), \(c \in [a;b]\)
-
D.
\(\int\limits_a^b {f(x)dx} = \int\limits_b^a {f(x)dx} \)
Họ tất cả các nguyên hàm của hàm số \(f(x) = 5{x^4} - 8{x^3} - 6x\) là
-
A.
\(F(x) = 5{x^4} - 4{x^4} - 2{x^2} + C\)
-
B.
\(F(x) = {x^5} + 2{x^4} - 3{x^2} + C\)
-
C.
\(F(x) = {x^5} - 2{x^4} - 3{x^2} + C\)
-
D.
\(F(x) = {x^5} - {x^4} - {x^2} + C\)
Cho \(\int\limits_0^{\frac{\pi }{2}} {f(x)dx} = 5\). Tính \(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f(x) + 2\sin x} \right]dx} \).
-
A.
\(I = 7\)
-
B.
\(I = 5 + \frac{\pi }{2}\)
-
C.
\(I = 3\)
-
D.
\(I = 5 + \pi \)
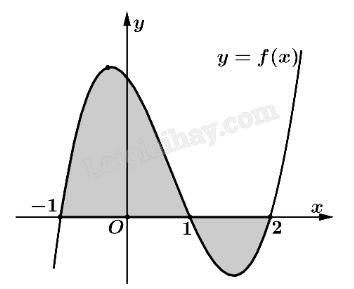
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), x = -1, x = 2. Mệnh đề nào dưới đây đúng?
-
A.
\(S = - \int\limits_{ - 1}^1 {f(x)dx} - \int\limits_1^2 {f(x)dx} \)
-
B.
\(S = \int\limits_{ - 1}^1 {f(x)dx} + \int\limits_1^2 {f(x)dx} \)
-
C.
\(S = - \int\limits_{ - 1}^1 {f(x)dx} + \int\limits_1^2 {f(x)dx} \)
-
D.
\(S = \int\limits_{ - 1}^1 {f(x)dx} - \int\limits_1^2 {f(x)dx} \)
Trong không gian Oxyz, cho A(1;1;-2), B(2;0;3), C(-2;4;1). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là
-
A.
\(2x - 2y + z + 2 = 0\)
-
B.
\(x + y - 2z - 6 = 0\)
-
C.
\(x + y - 2z + 2 = 0\)
-
D.
\(2x + 2y + z - 2 = 0\)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(2;-1;5) và nhận vecto \(\overrightarrow u = (2;3;1)\) làm vecto chỉ phương. Phương trình tham số của d là
-
A.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3 - t\\z = - 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 1 - 3t\\z = 5 - t\end{array} \right.\) \((t \in \mathbb{R})\)
Trong không gian Oxyz, cho mặt cầu có phương trình \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 9\). Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
-
A.
I(-3;1;-2); R = 3
-
B.
I(3;-1;2); R = 9
-
C.
I(-3;1;-2); R = 9
-
D.
I(3;-1;2); R = 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: \(\frac{x}{1} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 1}}{2}\) và d’: \(\frac{{x + 1}}{{ - 1}} = \frac{y}{1} = \frac{{z - 3}}{1}\). Góc giữa d và d’ bằng
-
A.
\({45^o}\)
-
B.
\({30^o}\)
-
C.
\({60^o}\)
-
D.
\({90^o}\)
Trong không gian Oxyz, đường thẳng d: \(\left\{ \begin{array}{l}x = - 1 + t\\y = 2 - 3t\\z = t\end{array} \right.\) và điểm A(2;3;1). Mặt phẳng (P) đi qua điểm A vuông góc với đường thẳng d có phương trình là
-
A.
2x + 3y + z + 6 = 0
-
B.
x – 3y + z + 6 = 0
-
C.
x – 3y + z – 6 = 0
-
D.
-x + 3y – z + 5 = 0
Cho hai biến cố A, B là hai biến cố độc lập với P(A) = 0,1997, P(B) = 0,1994. Tính P(A|B).
-
A.
0,1963
-
B.
0,1972
-
C.
0,1997
-
D.
0,1994
Khảo sát thị lực của học sinh ta thu được bảng số liệu sau:

Chọn ngẫu nhiên một bạn trong số 100 bạn học sinh nói trên. Gọi A là biến cố “Học sinh được chọn có tật khúc xạ” và B là biến cố “Học sinh được chọn là nữ”. Giá trị biểu thức \(P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\) bằng
-
A.
0,5
-
B.
0,4
-
C.
0,3
-
D.
0,24
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(4;0;0). Vùng phủ sóng của thiết bị có bán kính bằng 4.
a) Điểm M(4;2;2) thuộc vùng phủ sóng.
b) Tập hợp tất cả các điểm thuộc vùng phủ sóng của thiết bị được giới hạn bởi mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\).
c) Một bức tường được xây gần đó có phương trình (P): x + y – z = 6 sẽ chắn sóng của thiết bị.
d) Vùng nhận được tín hiệu trên mặt phẳng (P) là hình tròn có bán kính bằng 4.
Lớp 12A1 có 40 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ cầu lông, 16 học sinh tham gia câu lạc bộ đá bóng, 12 học sinh tham gia cả câu lạc bộ cầu lông và câu lạc bộ đá bóng. Chọn ngẫu nhiên một học sinh. Xét các biến cố sau:
A: “Học sinh được chọn ttham gia câu lạc bộ cầu lông”.
B: “Học sinh được chọn tham gia câu lạc bộ đá bóng”.
a) P(A) = 0,4.
b) P(B) = 0,625.
c) P(A|B) = 0,75.
d) Xác suất học sinh được chọn tham gia câu lạc bộ đá bóng, biết rằng học sinh đó đã tham gia câu lạc bộ cầu lông là 0,48.
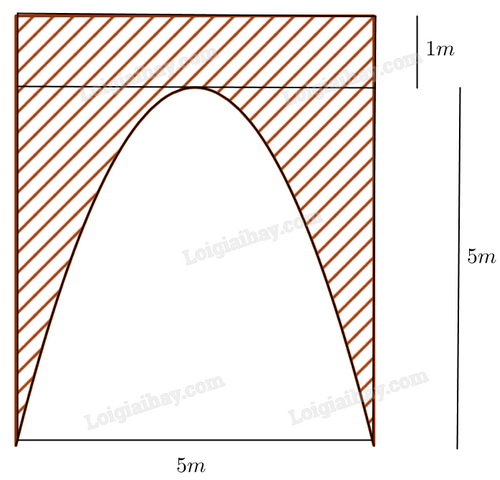
Nhà ông Hải có một cái cổng hình chữ nhật, lối vào cổng có dạng parabol có kích thước như hình vẽ. Ông Hải cần trang trí bề mặt (phần gạch chéo) của cổng. Hỏi ông Hải cần bao nhiêu tiền (đơn vị: triệu đồng) để trang trí, biết giá thành trang trí là 1200000 đồng/\({m^2}\)?
Giả sử tỉ lệ người dân của một tỉnh nghiện thuốc lá là 25%; tỉ lệ người mắc bệnh phổi trong số người nghiện thuốc lá là 72%, tỉ lệ người không mắc bệnh phổi trong số người không nghiện thuốc lá là 86%. Ta gặp ngẫu nhiên một người dân của tỉnh đó, tính xác suất người đó mắc bệnh phổi (làm tròn đến hàng phần trăm)?
Người ta truyền nhiệt cho một bình nuôi cấy vi sinh vật từ \({1^o}{\rm{C}}\). Tốc độ tăng nhiệt độ của bình tại thời điểm t phút \(\left( {0 \le t \le 5} \right)\) được cho bởi hàm số \(f(t) = 3{t^2}\) (\(^o{\rm{C}}\)/phút\()\). Biết rằng nhiệt độ của bình đó tại thời điểm t là một nguyên hàm của hàm số f(t). Tìm nhiệt độ của bình tại thời điểm 3 phút kể từ khi truyền nhiệt.
Trong không gian với trục hệ tọa độ Oxyz, cho điểm H(1;2;3) là trực tâm của \(\Delta ABC\) với A, B, C là ba điểm lần lượt nằm trên các trục Ox, Oy, Oz (khác gốc tọa độ). Phương trình mặt phẳng đi qua ba điểm A, B, C có dạng mx + ny + pz – 14 = 0 (\(m,n,p \in \mathbb{Z}\)). Khi đó m + n + p bằng bao nhiêu?
Lời giải và đáp án
Nguyên hàm của hàm số y = sinx + 2cosx là
-
A.
cosx – 2sinx + C
-
B.
-cosx + 2sinx + C
-
C.
cosx + 2sinx + C
-
D.
-cosx – 2sinx + C
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lượng giác \(\int {\cos xdx} = \sin x + C\), \(\int {\sin xdx} = - \cos x + C\).
\(\int {(\sin x + 2\cos x)dx} = - \cos x + 2\sin x + C\).
Cho hàm số f(x) liên tục trên đoạn [a;b]. Hãy chọn mệnh đề sai dưới đây.
-
A.
\(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \)
-
B.
\(\int\limits_a^b {kdx} = k(b - a)\), \(\forall k \in \mathbb{R}\)
-
C.
\(\int\limits_a^b {f(x)dx} = \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} \), \(c \in [a;b]\)
-
D.
\(\int\limits_a^b {f(x)dx} = \int\limits_b^a {f(x)dx} \)
Đáp án : D
Áp dụng tính chất của tích phân.
Ta có \(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \) nên \(\int\limits_a^b {f(x)dx} = \int\limits_b^a {f(x)dx} \) sai.
Họ tất cả các nguyên hàm của hàm số \(f(x) = 5{x^4} - 8{x^3} - 6x\) là
-
A.
\(F(x) = 5{x^4} - 4{x^4} - 2{x^2} + C\)
-
B.
\(F(x) = {x^5} + 2{x^4} - 3{x^2} + C\)
-
C.
\(F(x) = {x^5} - 2{x^4} - 3{x^2} + C\)
-
D.
\(F(x) = {x^5} - {x^4} - {x^2} + C\)
Đáp án : C
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {f(x)dx} = \int {\left( {5{x^4} - 8{x^3} - 6x} \right)} = 5.\frac{{{x^5}}}{5} - 8.\frac{{{x^4}}}{4} - 6.\frac{{{x^2}}}{2} + C = {x^5} - 2{x^4} - 3{x^2} + C\).
Cho \(\int\limits_0^{\frac{\pi }{2}} {f(x)dx} = 5\). Tính \(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f(x) + 2\sin x} \right]dx} \).
-
A.
\(I = 7\)
-
B.
\(I = 5 + \frac{\pi }{2}\)
-
C.
\(I = 3\)
-
D.
\(I = 5 + \pi \)
Đáp án : A
Áp dụng tính chất tích phân và công thức nguyên hàm của hàm số lượng giác.
\(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f(x) + 2\sin x} \right]dx} = I = \int\limits_0^{\frac{\pi }{2}} {f(x)dx} + 2\int\limits_0^{\frac{\pi }{2}} {\sin xdx} = 5 - 2\cos x\left| {\begin{array}{*{20}{c}}{^{\frac{\pi }{2}}}\\{_0}\end{array}} \right.\)
\( = 5 - 2\left( {\cos \frac{\pi }{2} - \cos 0} \right) = 5 - 2(0 - 1) = 7\).
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), x = -1, x = 2. Mệnh đề nào dưới đây đúng?

-
A.
\(S = - \int\limits_{ - 1}^1 {f(x)dx} - \int\limits_1^2 {f(x)dx} \)
-
B.
\(S = \int\limits_{ - 1}^1 {f(x)dx} + \int\limits_1^2 {f(x)dx} \)
-
C.
\(S = - \int\limits_{ - 1}^1 {f(x)dx} + \int\limits_1^2 {f(x)dx} \)
-
D.
\(S = \int\limits_{ - 1}^1 {f(x)dx} - \int\limits_1^2 {f(x)dx} \)
Đáp án : D
Áp dụng công thức tính diện tích hình phẳng: \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
\(S = \int\limits_{ - 1}^2 {\left| {f(x)} \right|dx} = \int\limits_{ - 1}^1 {f(x)dx} - \int\limits_1^2 {f(x)dx} \).
Trong không gian Oxyz, cho A(1;1;-2), B(2;0;3), C(-2;4;1). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là
-
A.
\(2x - 2y + z + 2 = 0\)
-
B.
\(x + y - 2z - 6 = 0\)
-
C.
\(x + y - 2z + 2 = 0\)
-
D.
\(2x + 2y + z - 2 = 0\)
Đáp án : A
Mặt phẳng qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} \) làm vecto pháp tuyến.
Mặt phẳng qua A(1;1;-2) và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} = ( - 4;4; - 2)\) làm vecto pháp tuyến có phương trình là:
\( - 4(x - 1) + 4(y - 1) - 2(z + 2) = 0 \Leftrightarrow - 4x + 4y - 2z - 4 = 0 \Leftrightarrow 2x - 2y - z + 2 = 0\).
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(2;-1;5) và nhận vecto \(\overrightarrow u = (2;3;1)\) làm vecto chỉ phương. Phương trình tham số của d là
-
A.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)\(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - t\\z = 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3 - t\\z = - 1 + 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 1 - 3t\\z = 5 - t\end{array} \right.\) \((t \in \mathbb{R})\)
Đáp án : C
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) có phương trình là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
d đi qua điểm M(2;-1;5) có vecto chỉ phương \(\overrightarrow u = (2;3;1)\) có phương trình là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in \mathbb{R})\).
Trong không gian Oxyz, cho mặt cầu có phương trình \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 9\). Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
-
A.
I(-3;1;-2); R = 3
-
B.
I(3;-1;2); R = 9
-
C.
I(-3;1;-2); R = 9
-
D.
I(3;-1;2); R = 3
Đáp án : A
Mặt cầu phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm I(a;b;c), bán kính R.
Mặt cầu phương trình \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 9\) có tâm I(-3;1;-2), bán kính R = 3.
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: \(\frac{x}{1} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 1}}{2}\) và d’: \(\frac{{x + 1}}{{ - 1}} = \frac{y}{1} = \frac{{z - 3}}{1}\). Góc giữa d và d’ bằng
-
A.
\({45^o}\)
-
B.
\({30^o}\)
-
C.
\({60^o}\)
-
D.
\({90^o}\)
Đáp án : D
Hai đường thẳng d, d’ có vecto chỉ phương lần lượt là \(\vec u,\vec u'\) có \(\cos \left( {d,d'} \right) = \frac{{\left| {\vec u.\vec u'} \right|}}{{\left| {\vec u} \right|.\left| {\vec u'} \right|}}\).
Vecto chỉ phương của d, d’ lần lượt là \(\vec u{\rm{\;}} = (1; - 1;2)\) và \(\vec u'{\rm{\;}} = ( - 1;1;1)\).
\(\cos \left( {d,d'} \right) = \frac{{\left| {\vec u.\vec u'} \right|}}{{\left| {\vec u} \right|.\left| {\vec u'} \right|}} = \frac{{\left| {1.( - 1) + ( - 1).1 + 2.1} \right|}}{{\sqrt {{1^2} + {{( - 1)}^2} + {2^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {1^2}} }} = 0\).
Vậy góc giữa d và d’ bằng \({90^o}\).
Trong không gian Oxyz, đường thẳng d: \(\left\{ \begin{array}{l}x = - 1 + t\\y = 2 - 3t\\z = t\end{array} \right.\) và điểm A(2;3;1). Mặt phẳng (P) đi qua điểm A vuông góc với đường thẳng d có phương trình là
-
A.
2x + 3y + z + 6 = 0
-
B.
x – 3y + z + 6 = 0
-
C.
x – 3y + z – 6 = 0
-
D.
-x + 3y – z + 5 = 0
Đáp án : B
Vecto pháp tuyến của mặt phẳng (P) là vecto chỉ phương của đường thẳng d.
d có vecto chỉ phương \(\overrightarrow u = (1; - 3;1)\), đồng thời là vecto pháp tuyến của (P).
Do đó (P): \(1(x - 2) - 3(y - 3) + 1(z - 1) = 0 \Leftrightarrow x - 3y + z + 6 = 0\).
Cho hai biến cố A, B là hai biến cố độc lập với P(A) = 0,1997, P(B) = 0,1994. Tính P(A|B).
-
A.
0,1963
-
B.
0,1972
-
C.
0,1997
-
D.
0,1994
Đáp án : C
Áp dụng công thức tính xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\).
Vì A, B là hai biến cố độc lập nên P(AB) = P(A).P(B).
Áp dụng công thức: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,1997.0,1994}}{{0,1994}} = 0,1997\).
Khảo sát thị lực của học sinh ta thu được bảng số liệu sau:

Chọn ngẫu nhiên một bạn trong số 100 bạn học sinh nói trên. Gọi A là biến cố “Học sinh được chọn có tật khúc xạ” và B là biến cố “Học sinh được chọn là nữ”. Giá trị biểu thức \(P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\) bằng
-
A.
0,5
-
B.
0,4
-
C.
0,3
-
D.
0,24
Đáp án : C
Áp dụng công thức xác suất toàn phần.
Có 18 + 12 = 30 học sinh bị tật khúc xạ nên \(P(A) = \frac{{30}}{{100}} = 0,3\).
Theo công thức xác suất toàn phần: \(P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = P\left( A \right) = 0,3\).
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(4;0;0). Vùng phủ sóng của thiết bị có bán kính bằng 4.
a) Điểm M(4;2;2) thuộc vùng phủ sóng.
b) Tập hợp tất cả các điểm thuộc vùng phủ sóng của thiết bị được giới hạn bởi mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\).
c) Một bức tường được xây gần đó có phương trình (P): x + y – z = 6 sẽ chắn sóng của thiết bị.
d) Vùng nhận được tín hiệu trên mặt phẳng (P) là hình tròn có bán kính bằng 4.
a) Điểm M(4;2;2) thuộc vùng phủ sóng.
b) Tập hợp tất cả các điểm thuộc vùng phủ sóng của thiết bị được giới hạn bởi mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\).
c) Một bức tường được xây gần đó có phương trình (P): x + y – z = 6 sẽ chắn sóng của thiết bị.
d) Vùng nhận được tín hiệu trên mặt phẳng (P) là hình tròn có bán kính bằng 4.
a) Áp dụng biểu thức tính khoảng cách giữa hai điểm. Nếu khoảng cách đó nhỏ hơn bán kính phủ sóng thì điểm M thuộc vùng phủ sóng.
b) Áp dụng quy tắc lập phương trình mặt cầu biết tâm và bán kính.
c) Tính khoảng cách từ điểm A tới mặt phẳng (P). Nếu khoảng cách đỏ nhỏ nhỏ hơn bán kính phủ sóng thì bức tường chắn được sóng của thiết bị.
d) Áp dụng định lí Pythagore.
a) Đúng. \(AM = \sqrt {{{(4 - 4)}^2} + {{(2 - 0)}^2} + {{(2 - 0)}^2}} = 2\sqrt 2 < 4\).
Khoảng cách từ M đến A nhỏ hơn bán kính phủ sóng nên M thuộc vùng phủ sóng.
b) Sai. Vùng phủ sóng là mặt cầu tâm A(4;0;0), bán kính R = 4 nên có phương trình:
\({\left( {x - 4} \right)^2} + {y^2} + {z^2} = 16\).
c) Đúng. \(d\left( {A,(P)} \right) = \frac{{\left| {1.4 + 1.0 - 1.0 - 6} \right|}}{{\sqrt {{1^2} + {1^2} + {{( - 1)}^2}} }} = \frac{{2\sqrt 3 }}{3} < 4\).
Vì khoảng cách từ bức tường tới thiết bị phát sóng nhỏ hơn bán kính phủ sóng nên bức tường đó chắn được sóng của thiết bị.
d) Sai. Bán kính vùng nhận được tín hiệu trên mặt phẳng (P) là \(\sqrt {{4^2} - {{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}} = \frac{{2\sqrt {33} }}{3}\).
Lớp 12A1 có 40 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ cầu lông, 16 học sinh tham gia câu lạc bộ đá bóng, 12 học sinh tham gia cả câu lạc bộ cầu lông và câu lạc bộ đá bóng. Chọn ngẫu nhiên một học sinh. Xét các biến cố sau:
A: “Học sinh được chọn ttham gia câu lạc bộ cầu lông”.
B: “Học sinh được chọn tham gia câu lạc bộ đá bóng”.
a) P(A) = 0,4.
b) P(B) = 0,625.
c) P(A|B) = 0,75.
d) Xác suất học sinh được chọn tham gia câu lạc bộ đá bóng, biết rằng học sinh đó đã tham gia câu lạc bộ cầu lông là 0,48.
a) P(A) = 0,4.
b) P(B) = 0,625.
c) P(A|B) = 0,75.
d) Xác suất học sinh được chọn tham gia câu lạc bộ đá bóng, biết rằng học sinh đó đã tham gia câu lạc bộ cầu lông là 0,48.
Áp dụng công thức tính xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\).
a) Sai. Có 25 trong tổng số 40 học sinh tham gia câu lạc bộ cầu lông nên \(P(A) = \frac{{25}}{{40}} = 0,625\).
b) Sai. Có 16 trong tổng số 40 học sinh tham gia câu lạc bộ đá bóng nên \(P(B) = \frac{{16}}{{40}} = 0,4\).
c) Đúng. Xác suất chọn được học sinh tham gia cả hai câu lạc bộ là \(P(AB) = \frac{{12}}{{40}} = 0,3\).
Ta có \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,3}}{{0,4}} = 0,75\).
d) Đúng. Ta có \(P(B|A) = \frac{{P(AB)}}{{P(A)}} = \frac{{0,3}}{{0,625}} = 0,48\).
Nhà ông Hải có một cái cổng hình chữ nhật, lối vào cổng có dạng parabol có kích thước như hình vẽ. Ông Hải cần trang trí bề mặt (phần gạch chéo) của cổng. Hỏi ông Hải cần bao nhiêu tiền (đơn vị: triệu đồng) để trang trí, biết giá thành trang trí là 1200000 đồng/\({m^2}\)?

Gắn hệ trục tọa độ phù hợp. Từ các điểm thuộc đồ thị, tìm phương trình của parabol rồi áp dụng công thức tính diện tích bằng tích phân.
Gắn hệ trục tọa độ Oxy như hình.
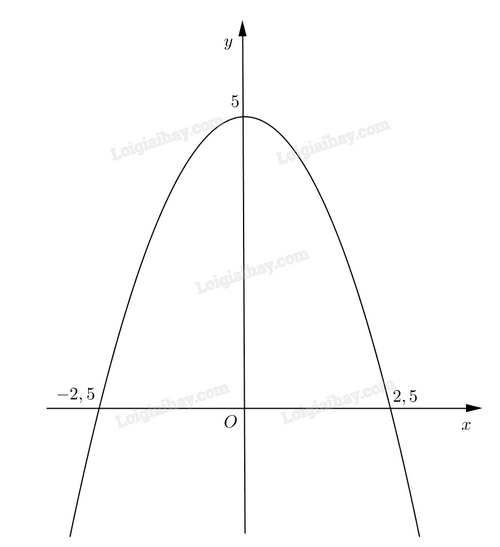
Giả sử parabol có phương trình \(y = a{x^2} + bx + c\) (a < 0).
Vì parabol đi qua các điểm (0;5), (-2,5;0), (2,5;0) nên ta có:
\(\left\{ \begin{array}{l}5 = a{.0^2} + b.0 + c\\0 = a.2,{5^2} + b.2,5 + c\\0 = a.{( - 2,5)^2} + b.( - 2,5) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{4}{5}\\b = 0\\c = 5\end{array} \right. \Rightarrow y = - \frac{4}{5}{x^2} + 5\).
Diện tích lối vào giới hạn bởi cổng là: \({S_1} = \int\limits_{ - 2,5}^{2,5} {\left( { - \frac{4}{5}{x^2} + 5} \right)dx} = \frac{{50}}{3}\) \(\left( {{m^2}} \right)\).
Diện tích toàn bộ hình chữ nhật là 5.6 = 30 \(\left( {{m^2}} \right)\).
Diện tích phần gạch chéo là: \({S_2} = S - {S_1} = 30 - \frac{{50}}{3} = \frac{{40}}{3}\) \(\left( {{m^2}} \right)\).
Số tiền cần để trang trí là \(\frac{{40}}{3}.1200000 = 16000000\) đồng = 16 triệu đồng.
Giả sử tỉ lệ người dân của một tỉnh nghiện thuốc lá là 25%; tỉ lệ người mắc bệnh phổi trong số người nghiện thuốc lá là 72%, tỉ lệ người không mắc bệnh phổi trong số người không nghiện thuốc lá là 86%. Ta gặp ngẫu nhiên một người dân của tỉnh đó, tính xác suất người đó mắc bệnh phổi (làm tròn đến hàng phần trăm)?
Áp dụng công thức xác suất toàn phần: \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\bar A} \right).P\left( {B|\bar A} \right)\).
A: “Người đó nghiện thuốc lá”. P(A) = 25% = 0,25.
\(\overline A \): “Người đó không nghiện thuốc lá”. P(\(\overline A \)) = 1 – 25% = 75% = 0,75.
B: “Người đó mắc bệnh phổi”.
Có 72% số người hút thuốc lá bị bệnh phổi nên P(B|A) = 72% = 0,72.
Có 86% số người không hút thuốc lá không bị bệnh phổi nên số người không hút thuốc lá bị bệnh phổi là 1 – 86% = 14% = 0,14, khi đó P(B|\(\overline A \)) = 0,14.
Áp dụng công thức: \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\bar A} \right).P\left( {B|\bar A} \right) \)
\(= 0,25.0,72 + 0,75.0,14 = 0,285 \approx 0,29\).
Người ta truyền nhiệt cho một bình nuôi cấy vi sinh vật từ \({1^o}{\rm{C}}\). Tốc độ tăng nhiệt độ của bình tại thời điểm t phút \(\left( {0 \le t \le 5} \right)\) được cho bởi hàm số \(f(t) = 3{t^2}\) (\(^o{\rm{C}}\)/phút\()\). Biết rằng nhiệt độ của bình đó tại thời điểm t là một nguyên hàm của hàm số f(t). Tìm nhiệt độ của bình tại thời điểm 3 phút kể từ khi truyền nhiệt.
Tính F(3) với \(F(t) = \int {f(t)dt} \).
Nhiệt độ của bình là: \(F(t) = \int {f(t){\rm{d}}t} = \int {3{t^2}{\rm{d}}t} = {t^3} + C\).
Vì người ta bắt đầu truyền nhiệt cho bình nuôi cấy từ \({1^o}{\rm{C}}\) nên:
\(F(0) = 1 \Leftrightarrow {0^3} + C = 1 \Leftrightarrow C = 1\).
Suy ra \(F\left( t \right) = {t^3} + 1\).
Vậy nhiệt độ của bình tại thời điểm 3 phút kể từ khi truyền nhiệt là \(F\left( 3 \right) = {3^3} + 1 = 28\) \({(^o}C)\).
Trong không gian với trục hệ tọa độ Oxyz, cho điểm H(1;2;3) là trực tâm của \(\Delta ABC\) với A, B, C là ba điểm lần lượt nằm trên các trục Ox, Oy, Oz (khác gốc tọa độ). Phương trình mặt phẳng đi qua ba điểm A, B, C có dạng mx + ny + pz – 14 = 0 (\(m,n,p \in \mathbb{Z}\)). Khi đó m + n + p bằng bao nhiêu?
Lập phương trình mặt chắn (ABC), kết hợp với hệ \(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\end{array} \right.\) để tìm tọa độ ba điểm A, B, C.
Giả sử: A(a;0;0), B(0;b;0), C(0;0;c).
Ta có \(\overrightarrow {AH} \left( {1 - a;2;3} \right)\), \(\overrightarrow {BH} \left( {1;2 - b;3} \right)\), \(\overrightarrow {BC} \left( {0;\, - b;\,c} \right)\), \(\overrightarrow {AC} \left( { - a;\,0;\,c} \right)\).
Do H là trực tâm \(\Delta ABC\) nên ta có: \(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2b + 3c = 0\\ - a + 3c = 0\end{array} \right.\)
Phương trình mặt phẳng (ABC): \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) và do \(H \in \left( {ABC} \right)\) nên \(\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 1\).
Do đó ta có hệ phương trình: \(\left\{ \begin{array}{l} - 2b + 3c = 0\\ - a + 3c = 0\\\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2b\\c = \frac{{2b}}{3}\\\frac{1}{{2b}} + \frac{2}{b} + \frac{9}{{2b}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 14\\b = 7\\c = \frac{{14}}{3}\end{array} \right.\)
Phương trình mặt phẳng (ABC): \(\frac{x}{{14}} + \frac{y}{7} + \frac{{3z}}{{14}} = 1 \Leftrightarrow x + 2y + 3z - 14 = 0\).
Vậy m + n + p = 1 + 2 + 3 = 6.
Xét dấu của biểu thức để phá dấu trị tuyệt đối.
\(A = \int\limits_{ - 2}^2 {\left| {{x^2} - 1} \right|{\rm{d}}x} \).
Xét \(f\left( x \right) = {x^2} - 1\) trên đoạn \(\left[ { - 2;2} \right]\).
Cho \(f\left( x \right) = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \in \left[ { - 2;2} \right]\\x = 1 \in \left[ { - 2;2} \right]\end{array} \right.\)
Bảng xét dấu:

\(A = \int\limits_{ - 2}^2 {\left| {{x^2} - 1} \right|{\rm{d}}x} \)
\(= \int\limits_{ - 2}^{ - 1} {\left( {{x^2} - 1} \right){\rm{d}}x} + \int\limits_{ - 1}^1 {\left( {1 - {x^2}} \right){\rm{d}}x} + \int\limits_1^2 {\left( {{x^2} - 1} \right){\rm{d}}x} \)
\( = \left. {\left( {\frac{{{x^3}}}{3} - x} \right)} \right|_{ - 2}^{ - 1} + \left. {\left( {x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 1}^1 + \left. {\left( {\frac{{{x^3}}}{3} - x} \right)} \right|_1^2\)
\(= \left[ {\frac{2}{3} - \left( { - \frac{2}{3}} \right)} \right] + \left[ {\frac{2}{3} - \left( { - \frac{2}{3}} \right)} \right] + \left[ {\frac{2}{3} - \left( { - \frac{2}{3}} \right)} \right] = 4\).
Gọi \({\vec u_1}\), \({\vec u_2}\) lần lượt là các vecto chỉ phương của \({\Delta _1}\), \({\Delta _2}\).
Viết phương trình đường thẳng d đi qua A(1;2;1) và có vecto chỉ phương \(\vec u = \left[ {{{\vec u}_1},{{\vec u}_2}} \right]\).
\({\Delta _1}\) có một vecto chỉ phương là \({\vec u_1} = (1; - 1;1)\).
\({\Delta _2}\) có một vecto chỉ phương là \({\vec u_2} = (1;2; - 1)\).
Ta có \(\left\{ \begin{array}{l}d \bot {\Delta _1}\\d \bot {\Delta _2}\end{array} \right.\) nên d có một vecto chỉ phương là \(\vec u = \left[ {{{\vec u}_1},{{\vec u}_2}} \right]\).
Ta có \(\vec u = \left[ {{{\vec u}_1},{{\vec u}_2}} \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 1}&1\\2&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&1\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 1}\\1&2\end{array}} \right|} \right) = ( - 1;2;3)\).
Vậy đường thẳng d đi qua A(1;2;1) và có vecto chỉ phương \(\vec u = ( - 1;2;3)\) có phương trình là \(\frac{{x - 1}}{{ - 1}} = \frac{{y - 2}}{2} = \frac{{z - 1}}{3}\).
- Viết phương trình đường thẳng d đi qua điểm A và có một vectơ chỉ phương \(\overrightarrow u \).
- Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa. B thuộc d nên tính tọa độ của B theo t.
- Để B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì OB = 417. Từ đó có phương trình theo ẩn t, giải phương trình tính t.
- Thay giá trị t tính được để tìm tọa độ B, so sánh giá trị và được ra kết luận.
Phương trình tham số của đường thẳng d đi qua A(-688;-185;8) và nhận \(\overrightarrow u = \left( {91;75;0} \right)\) làm vecto chỉ phương là \(\left\{ \begin{array}{l}x = - 688 + 91t\\y = - 185 + 75t\\z = 8\end{array} \right.\).
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vì \(B \in d\) nên B(-688 + 91t; -185 + 75t; 8).
Vì \(B\) là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa nên
\(OB = 417 \Leftrightarrow \sqrt {{{\left( { - 688 + 91t} \right)}^2} + {{\left( { - 185 + 75t} \right)}^2} + {8^2}} = 417\)
\( \Leftrightarrow 13906{t^2} - 152966t + 333744 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 3}\\{t = 8}\end{array}} \right.\)
Với t = 3 thì B(-415;408) suy ra \(AB \approx 353,77\) km.
Với t = 8 thì B(-88;415;8) suy ra \(AB \approx 848,53\) km.
Do 353,77 < 848,53 vị trí máy bay xuất hiện sớm nhất là B(-415;40;8).
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.










Danh sách bình luận