Trong không gian Oxyz, viết phương trình đường thẳng d đi qua điểm M(1;2;1), đồng thời vuông góc với cả hai đường thẳng \({\Delta _1}:\frac{{x - 2}}{1} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 1}}{1}\) và \({\Delta _2}:\frac{{x + 1}}{1} = \frac{{y - 3}}{2} = \frac{{z - 1}}{{ - 1}}.\)
Gọi \({\vec u_1}\), \({\vec u_2}\) lần lượt là các vecto chỉ phương của \({\Delta _1}\), \({\Delta _2}\).
Viết phương trình đường thẳng d đi qua A(1;2;1) và có vecto chỉ phương \(\vec u = \left[ {{{\vec u}_1},{{\vec u}_2}} \right]\).
\({\Delta _1}\) có một vecto chỉ phương là \({\vec u_1} = (1; - 1;1)\).
\({\Delta _2}\) có một vecto chỉ phương là \({\vec u_2} = (1;2; - 1)\).
Ta có \(\left\{ \begin{array}{l}d \bot {\Delta _1}\\d \bot {\Delta _2}\end{array} \right.\) nên d có một vecto chỉ phương là \(\vec u = \left[ {{{\vec u}_1},{{\vec u}_2}} \right]\).
Ta có \(\vec u = \left[ {{{\vec u}_1},{{\vec u}_2}} \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 1}&1\\2&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&1\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 1}\\1&2\end{array}} \right|} \right) = ( - 1;2;3)\).
Vậy đường thẳng d đi qua A(1;2;1) và có vecto chỉ phương \(\vec u = ( - 1;2;3)\) có phương trình là \(\frac{{x - 1}}{{ - 1}} = \frac{{y - 2}}{2} = \frac{{z - 1}}{3}\).
Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho hai điểm phân biệt \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng \({A_1}{A_2}\).
b) Viết phương trình đường thẳng \({A_1}{A_2}\).
Trong không gian Oxyz, viết các phương trình tham số và chính tắc của đường thẳng \(\Delta \) đi qua \(A\left( {1;{\rm{ }}1;{\rm{ }}2} \right)\) và song song với đường thẳng \(d:\frac{{x - 3}}{2} = \frac{{y - 1}}{1} = \frac{{z + 5}}{3}\).
Trong không gian Oxyz, viết các phương trình tham số và chính tắc của đường thẳng \(\Delta \) đi qua \(A\left( {2; - 1;4} \right)\) và vuông góc với mặt phẳng \(\left( P \right):x + 3y - z - 1 = 0\).
Trong không gian Oxyz, cho điểm \(I\left( { - 1;2;1} \right)\) và mặt phẳng \(\left( P \right):2x - 2y - z - 5 = 0\). Viết phương trình đường thẳng d đi qua I và vuông góc với mặt phẳng (P).
Trong không gian Oxyz, cho điểm \(A\left( { - 1;1;2} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + t\\y = 3 - 2t\\z = - 1 + 2t\end{array} \right.\).
a) Viết phương trình đường thẳng d’ đi qua A và song song với đường thẳng d.
b) Viết phương trình mặt phẳng (P) chứa điểm A và đường thẳng d.
Trong không gian Oxyz, có một nguồn sáng phát ra từ điểm S(2; 3; 5) và một đoạn dây thẳng nối từ điểm A(1; 2; 1) đến điểm B(3; 1; 2). Dưới nguồn sáng, đoạn dây trên có bóng trên mặt phẳng (Oxy) là một đoạn thẳng. Tính độ dài đoạn thẳng đó.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {1;2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 3;5} \right)\). Xét điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) nằm trên \(\Delta \) (Hình 24).
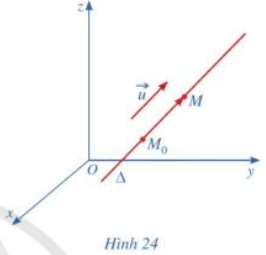
a) Nêu nhận xét về phương của hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \).
b) Có hay không số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \)?
c) Hãy biểu diễn x, y, z qua t.
d) Tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) có thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 3t\\z = 3 + 5t\end{array} \right.\) hay không?
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {1;2;3} \right)\) và \(B\left( {3;5;9} \right)\).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng AB.
c) Viết phương trình chính tắc của đường thẳng AB.
Viết phương trình tham số và phương trình chính tắc của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) \(\Delta \) đi qua điểm \(A\left( { - 1;3;2} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 2;3;4} \right)\).
b) \(\Delta \) đi qua hai điểm \(M\left( {2; - 1;3} \right)\) và \(N\left( {3;0;4} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S. ABCD có các đỉnh lần lượt là \(S\left( {0;0;\frac{{a\sqrt 3 }}{2}} \right),A\left( {\frac{a}{2};0;0} \right),B\left( { - \frac{a}{2};0;0} \right),C\left( { - \frac{a}{2};a;0} \right),D\left( {\frac{a}{2};a;0} \right)\) với \(a > 0\) (Hình 36).
a) Xác định tọa độ của các vectơ \(\overrightarrow {SA} ,\overrightarrow {CD} \). Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).
b) Chỉ ra một vectơ pháp tuyến của mặt phẳng (SAC). Từ đó tính góc đường thẳng SD và mặt phẳng (SAC) (làm tròn kết quả đến hàng đơn vị của độ).
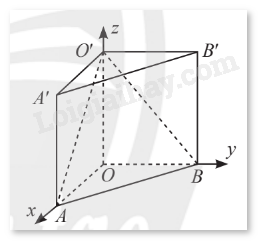
Trong không gian \(Oxyz\), cho hình lăng trụ \(OAB.O'A'B'\). Biết \(O\) là gốc toạ độ, \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\). Viết phương trình các mặt phẳng \(\left( {O'AB} \right)\) và \(\left( {O'A'B'} \right)\).
Cho đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right).\)
a) Tìm một vectơ chỉ phương của \(d.\)
b) Viết phương trình tham số và phương trình chính tắc của \(d.\)
Viết phương trình tham số và phương trình chính tắc của đường thẳng \(MN\), biết \(M\left( {2;0; - 1} \right)\) và \(N\left( {4;3;1} \right).\)
Lập phương trình tham số và phương trình chính tắc của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) \(\Delta \) đi qua điểm \(A\left( {2; - 5;7} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 2;3;4} \right)\);
b) \(\Delta \) đi qua hai điểm \(M\left( { - 1;0;4} \right)\) và \(N\left( {2;5;3} \right)\).
c) \(\Delta \) đi qua điểm \(B\left( {3;2; - 1} \right)\) và vuông góc với mặt phẳng \(\left( P \right):2x - 5y + 6z - 7 = 0\).
Trong không gian Oxyz, cho ba điểm \(A\left( {0;0;2} \right)\), \(B\left( {1;2;1} \right)\), \(C\left( {2;3;4} \right)\).
a) Viết phương trình tham số, phương trình chính tắc của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng d, đi qua điểm C và song song với AB.
Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + 3t\\y = - 1 - t\\z = - 3 + 2t\end{array} \right.\) và mặt phẳng \(\left( P \right):x - y - z = 0\)
a) Tìm tọa độ giao điểm I của đường thẳng d và mặt phẳng \(\left( P \right)\).
b) Viết phương trình đường thẳng \(d'\) nằm trên mặt phẳng \(\left( P \right)\) sao cho \(d'\) cắt và vuông góc với \(d\).
Trong không gian Oxyz, cho hai đường thẳng:
\(\Delta :\left\{ \begin{array}{l}x = 2 + 3t\\y = 1 + 2t\\z = - 1 + t\end{array} \right.\) và \(\Delta ':\left\{ \begin{array}{l}x = - 1 + s\\y = 2 - s\\z = 3 + 2s\end{array} \right.\)
a) Xét vị trí tương đối của hai đường thẳng \(\Delta \) và \(\Delta '\).
b) Tính côsin của góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\).
c) Viết phương trình đường thẳng d đi qua \(A\left( { - 3;2;2} \right)\) và song song với đường thẳng \(\Delta \).
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho hai điểm \(A\left( {2;1; - 2} \right),B\left( { - 2; - 2; - 9} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = - 1 + t\\z = - t\end{array} \right.\).
a) Điểm \(A\) thuộc đường thẳng \(d\).
b) Điểm \(B\) thuộc đường thẳng \(d\).
c) Đường thẳng \(AB\) vuông góc với \(d\).
d) \(\overrightarrow {AB} = \left( {4;3; - 7} \right)\).
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho hai đường thẳng \(d:\frac{{x + 2}}{2} = \frac{y}{{ - 1}} = \frac{{z + 1}}{2}\) và \(d':\frac{{x - 2}}{3} = \frac{y}{{ - 4}} = \frac{{z - 1}}{{ - 5}}\).
a) Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;0; - 1} \right)\).
b) Đường thẳng \(d\) có vectơ chỉ phương \(\overrightarrow a = \left( { - 4;2; - 4} \right)\).
c) Đường thẳng \(d'\) không đi qua điểm \(N\left( {2;0;1} \right)\).
d) Đường thẳng \(d\) vuông góc với \(d'\).
Trong không gian Oxyz, cho tam giác OAB với \(A(2; - 3;4)\), \(B( - 4;5;0)\). Viết phương trình tham số và phương trình chính tắc (nếu có) của đường thẳng AB và đường thẳng chứa đường trung tuyến kẻ từ O của tam giác OAB.
Trong không gian Oxyz, cho đường thẳng \(d\) qua hai điểm phân biệt \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\).
a) Vectơ \(\overrightarrow {AB} \) có phải là một vectơ chỉ phương của \(d\) không? Vì sao?
b) Viết phương trình tham số của đường thẳng \(d\).
c) Giả sử \({x_B} \ne {x_A},{y_B} \ne {y_A}\) và \({z_B} \ne {z_A}\), hãy viết phương trình chính tắc của \(d\).
Viết phương trình tham số và phương trình chính tắc (nếu có) của đường thẳng \(d\) trong mỗi trường hợp sau:
a) \(d\) đi qua điểm \(M(5;4;1)\) và có vectơ chỉ phương \(\vec a = (2; - 3;1)\).
b) \(d\) đi qua hai điểm \(P(1;2;3)\) và \(Q(5;4;4)\).
c) \(d\) đi qua điểm \(B(2;0; - 3)\) và song song với đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = - 3 + 3t}\\{z = 4}\end{array}} \right.\).
d) \(d\) đi qua điểm \(A( - 2;3;1)\) và song song với đường thẳng \(\Delta ':\frac{{x - 3}}{2} = \frac{{y + 1}}{1} = \frac{{z - 4}}{3}\).
Cho hình chóp S.ABCD với ABCD là hình bình hành, \(S(3; - 2;4)\), \(A(3;4;5)\), \(B(8;8;6)\), \(C(7;6;3)\). Viết phương trình đường thẳng chứa cạnh SB và đường thẳng chứa cạnh đáy AD của hình chóp.
Cho đường thẳng \(d\):
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 2 - 2t}\\{y = 3 + 3t{\mkern 1mu} (t \in \mathbb{R})}\\{z = 6 + 4t}\end{array}} \right.\)
a) Tìm tọa độ điểm \(A\) thuộc \(d\), biết \(OA = 7\).
b) Tìm tọa độ điểm \(H\) là hình chiếu vuông góc của điểm \(O\) trên \(d\) và tính khoảng cách từ \(O\) đến \(d\).
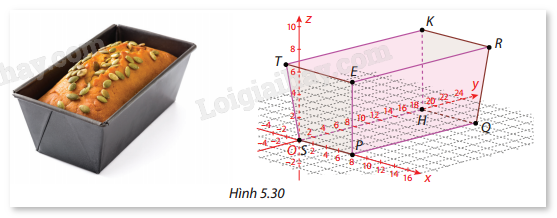
Một khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn.
Cho đường thẳng d: \(\frac{{x + 3}}{2} = \frac{{y - 1}}{1} = \frac{z}{3}\) và d’: \(\left\{ \begin{array}{l}x = 4 + 2t\\y = 2 + t\\z = - 1 + 3t\end{array} \right.\). Trong mỗi ý a), b), c), d), chọn phương án Đúng (Đ) hoặc Sai (S).
Cho đường thẳng d: \(\frac{{x - 1}}{2} = \frac{{y + 3}}{1} = \frac{{z + 1}}{{ - 1}}\) và mặt phẳng (P): x + 2y + 4z + 1 = 0. Trong mỗi ý a), b), c), d), chọn phương án Đúng (Đ) hoặc Sai (S).
Trên thiết kế trong không gian Oxyz, một con đường thuộc đường thẳng có phương trình d: \(\frac{x}{{ - 1}} = \frac{{y + 1}}{1} = \frac{{z - 2}}{1}\). Một chiếc ô tô đang đỗ được định vị có tọa độ (0;-1;2), một trung tâm thương mại có tọa độ (-1;0;3) và công viên có tọa độ (-2;1;4). Trong mỗi ý a), b), c), d), chọn phương án Đúng (Đ) hoặc Sai (S).
Trong không gian Oxyz, cho hai đường thẳng:
\(\Delta :\left\{ \begin{array}{l}x = 3\\y = 1 + t\\z = - 1 + 3t\end{array} \right.\) và \(\Delta ':\left\{ \begin{array}{l}x = 1 + s\\y = - 2 + 3s\\z = - 5\end{array} \right.\)
a) Xét vị trí tương đối của hai đường thẳng \(\Delta \) và \(\Delta '\).
b) Tính cosin góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\).
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(−2; 1; −1). Tìm góc giữa:
a) Hai mặt phẳng (ABC) và (BCD);
b) Hai đường thẳng AB và CD;
c) Đường thẳng AB và mặt phẳng (BCD).
