Đề thi giữa kì 1 Toán 12 - Đề số 2
Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
Đề bài
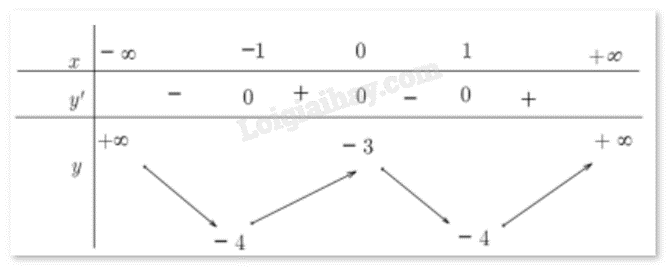
Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
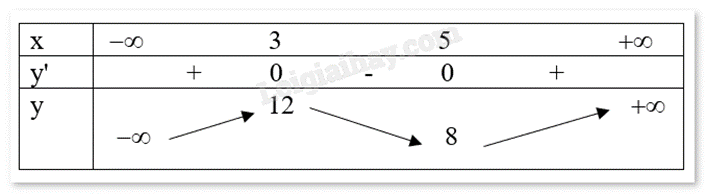
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
-
A.
\(( - \infty ;3)\)
-
B.
\((5; + \infty )\)
-
C.
\((3;5)\)
-
D.
\(\mathbb{R}\)
-
A.
\(y = \frac{{2x - 1}}{{x + 1}}\)
-
B.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
C.
\(y = \frac{{2x + 1}}{{x + 1}}\)
-
D.
\(y = \frac{{1 - 2x}}{{x - 1}}\)
Cho hàm số f(x) có đồ thị như hình dưới đây:
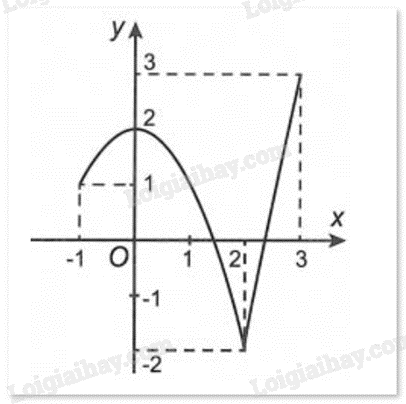
Giá trị lớn nhất của hàm số đã cho trên [-1;3] là:
-
A.
y = 1
-
B.
y = 2
-
C.
y = -2
-
D.
y = 3
-
A.
0
-
B.
2
-
C.
1
-
D.
4
Đồ thị \(y = \frac{{{x^2} - 3x + 2}}{{x - 1}}\) có tất cả bao nhiêu đường tiệm cận đứng?
-
A.
3
-
B.
1
-
C.
0
-
D.
2
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) là?
-
A.
(3;2)
-
B.
(-3;2)
-
C.
(-1;3)
-
D.
(1;-3)
Trong không gian cho điểm O và bốn điểm A, B, C, D không thẳng hàng. Điều kiện cần và đủ để A, B, C, D tạo thành hình bình hành là?
-
A.
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
-
B.
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
-
C.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \frac{1}{2}\overrightarrow {OD} \)
-
D.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \frac{1}{2}\overrightarrow {OD} \)
-
A.
\(y = {x^3} - 3{x^2} + 2\)
-
B.
\(y = - {x^3} + 3{x^2} + 2\)
-
C.
\(y = {x^3} + 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} + 2\)
Giá trị lớn nhất của hàm số \(\frac{{2x + 1}}{{x - 2}}\) trên đoạn \([ - \frac{1}{2};1]\) bằng:
-
A.
0
-
B.
\(\frac{1}{2}\)
-
C.
-3
-
D.
1
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ:
Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = {x^3} - 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} - 1\)
Công thức tính tích vô hướng của 2 vecto là?
-
A.
\(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow {a.} \overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
-
B.
\(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
-
C.
\(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
-
D.
\(\overrightarrow {a.} \overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Xét các vecto \(\overrightarrow x = 2\overrightarrow a - \overrightarrow b \); \(\overrightarrow y = - 4\overrightarrow a + 2\overrightarrow b \); \(\overrightarrow z = - 3\overrightarrow b - 2\overrightarrow c \). Chọn khẳng định đúng?
-
A.
Hai vecto \(\overrightarrow y ,\overrightarrow z \) cùng phương
-
B.
Hai vecto \(\overrightarrow x ,\overrightarrow y \) cùng phương
-
C.
Hai vecto \(\overrightarrow x ,\overrightarrow z \) cùng phương
-
D.
Ba vecto \(\overrightarrow x ,\overrightarrow y ,\overrightarrow z \) đồng phẳng.
a) Hàm số f(x) đồng biến trên mỗi khoảng (-1;0) và (0;1)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng -3
d) Đồ thị hàm số không có đường tiệm cận
Cho hàm số \(y=x - \sqrt {{x^2} + 1} \).
a) Hàm số đã cho nghịch biến trên R
b) Đồ thị hàm số đã cho có cực tiểu
c) Đồ thị hàm số đã cho có 1 tiệm cận ngang
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
a) \(\overrightarrow {AB} = \overrightarrow {DC} \)
b) \(\overrightarrow {AC} = \overrightarrow {BD} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 2\overrightarrow {SO} \)
Cho hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có \(AB = a\), \(BC = 2a\), \(A{A_1} = 3a\).
a) \(\left( {\overrightarrow {A{B_1}} ;\overrightarrow {{C_1}D} } \right) = {45^o}\)
b) \(\overrightarrow {{A_1}B} .\overrightarrow {{D_1}D} = 9{a^2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {{C_1}{A_1}} .\overrightarrow {{C_1}{B_1}} \)
d) \(\overrightarrow {{A_1}{D_1}} .\overrightarrow {{C_1}C} = 0\)
Giá trị lớn nhất của hàm số \(y = x{(5 - 2x)^2}\) trên [0;3] là một phân số có dạng \(\frac{a}{b}\). Tính a + 2b.
Đáp án:
Khoảng cách từ điểm A(-5;1) đến đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}}\) là bao nhiêu?
Đáp án:
Trong không gian Oxyz, cho hình bình hành ABCD. Biết A(1;0;1), B(2;1;2), và D(1;-1;1). Tọa độ điểm C là (a;b;c). Tính tổng a + b + c.
Đáp án:
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G(x) = 0,025{x^2}(30 - x)\), trong đó x là liều lượng thuốc được tiêm cho bênh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án:
Một con nhện đang treo mình dưới một sợi tơ theo phương thẳng đứng thì bị một cơn gió thổi theo phương ngang làm dây treo lệch đi so với phương thẳng đứng một góc \({30^o}\). Biết trọng lượng của con nhện là P = 0,1 N. Xác định độ lớn của lực mà gió tác dụng lên con nhện ở vị trí cân bằng (kết quả làm tròn đến hàng phần trăm).
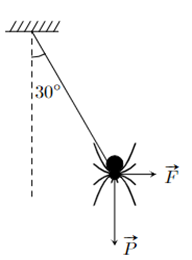
Đáp án:
Hình vẽ dưới đây mô tả một sân cầu long với kích thước theo chuẩn quốc tế. Ta chọn hệ trục Oxyz cho sân đó như hình vẽ (đơn vị trên mỗi trục là mét). Giả sử AB là một trụ cầu lông để căng lưới. Gọi (x;y;z) là tọa độ của \(\overrightarrow {AB} \). Tính x + y + x.
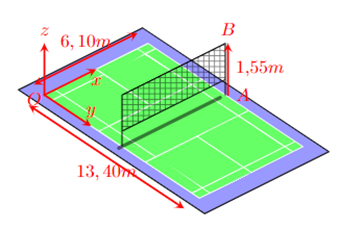
Đáp án:
Lời giải và đáp án
Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
-
A.
\(( - \infty ;3)\)
-
B.
\((5; + \infty )\)
-
C.
\((3;5)\)
-
D.
\(\mathbb{R}\)
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Quan sát bảng biến thiên thấy y’ < 0 trên khoảng (3;5) nên hàm số nghịch biến trên khoảng (3;5).
-
A.
\(y = \frac{{2x - 1}}{{x + 1}}\)
-
B.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
C.
\(y = \frac{{2x + 1}}{{x + 1}}\)
-
D.
\(y = \frac{{1 - 2x}}{{x - 1}}\)
Đáp án : A
Quan sát đồ thị và nhận xét.
Nhìn vào đồ thị thấy ngay tiệm cận đứng x = -1, tiệm cận ngang y = 2. Loại đáp án B, D.
Đồ thị hàm số đi qua điểm (0;-1). Thay x = 0 vào đáp án A, C để tính y, thấy ở đồ thị đáp án A y = -1.
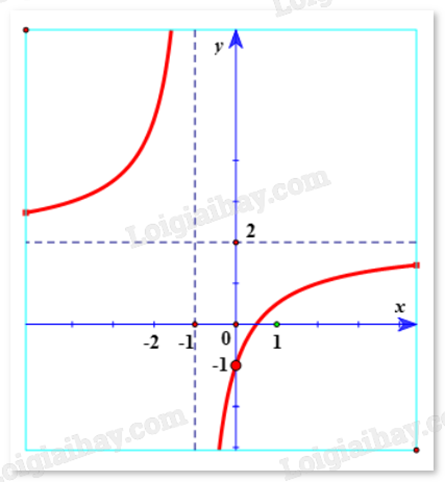
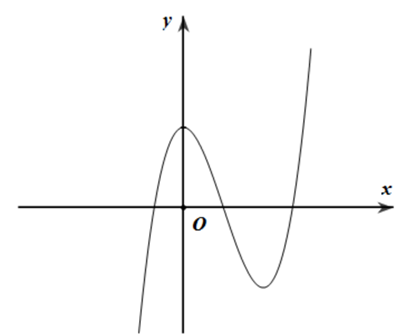
Cho hàm số f(x) có đồ thị như hình dưới đây:
Giá trị lớn nhất của hàm số đã cho trên [-1;3] là:
-
A.
y = 1
-
B.
y = 2
-
C.
y = -2
-
D.
y = 3
Đáp án : D
Quan sát đồ thị và nhận xét.
Hàm số đạt giá trị lớn nhất y = 3.
-
A.
0
-
B.
2
-
C.
1
-
D.
4
Đáp án : D
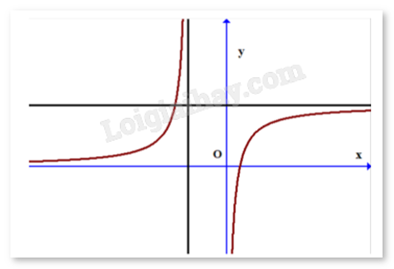
Quan sát đồ thị và nhận xét.
Có tất cả 4 đường tiệm cận.
Đồ thị \(y = \frac{{{x^2} - 3x + 2}}{{x - 1}}\) có tất cả bao nhiêu đường tiệm cận đứng?
-
A.
3
-
B.
1
-
C.
0
-
D.
2
Đáp án : B
Tìm đường tiệm cận đứng thông qua giới hạn của hàm số.
Ta có: \(y = \frac{{{x^2} - 3x + 2}}{{{x^2} - 1}} = \frac{{(x - 1)(x - 2)}}{{(x - 1)(x + 1)}} = \frac{{x - 2}}{{x + 1}}.\)
\( \Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{x - 2}}{{x + 1}} = - \infty .\)
Vậy x = -1 là tiệm cận đứng của đồ thị hàm số.
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) là?
-
A.
(3;2)
-
B.
(-3;2)
-
C.
(-1;3)
-
D.
(1;-3)
Đáp án : A
Tìm giao điểm hai đường tiệm cận của đồ thị hàm số.
Vậy tâm đối xứng của đồ thị có tọa độ (3;2).
Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } y = 2\) suy ra đuờng thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
Ta có \(\mathop {\lim }\limits_{x \to {3^ + }} y = + \infty ;\) \(\mathop {\lim }\limits_{x \to {3^ - }} y = - \infty \) suy ra đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
Vậy tâm đối xứng của đồ thị có tọa độ (3;2).
Trong không gian cho điểm O và bốn điểm A, B, C, D không thẳng hàng. Điều kiện cần và đủ để A, B, C, D tạo thành hình bình hành là?
-
A.
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
-
B.
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
-
C.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \frac{1}{2}\overrightarrow {OD} \)
-
D.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \frac{1}{2}\overrightarrow {OD} \)
Đáp án : B
Dựa vào lí thuyết phép cộng (trừ) các vecto trong không gian, các vecto bằng nhau, đối nhau, quy tắc hình bình hành.
Điều kiện cần và đủ để ABCD là hình bình hành là: \(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC} \) (quy tắc hình bình hành).
Với mọi điểm O bất kì khác A, B, C, D, ta có:
\(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC} \Leftrightarrow \overrightarrow {OD} - \overrightarrow {OB} = \overrightarrow {OA} - \overrightarrow {OB} + \overrightarrow {OC} - \overrightarrow {OB} \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} .\)\(\)
-
A.
\(y = {x^3} - 3{x^2} + 2\)
-
B.
\(y = - {x^3} + 3{x^2} + 2\)
-
C.
\(y = {x^3} + 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} + 2\)
Đáp án : A
Quan sát đồ thị và nhận xét.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên a > 0. Loại B, D.
Hàm số đạt cực trị tại \({x_1} = 0\) và \({x_2} > 0\).
Xét hàm số \(y = {x^3} + 3{x^2} + 2\) có \(y' = 3{x^2} + 6x = 0\) suy ra x = -2 hoặc x = 0.
Suy ra \(y = {x^3} + 3{x^2} + 2\) đạt cực trị tại \({x_1} = 0\) và \({x_2} < 0\). Loại C.
Giá trị lớn nhất của hàm số \(\frac{{2x + 1}}{{x - 2}}\) trên đoạn \([ - \frac{1}{2};1]\) bằng:
-
A.
0
-
B.
\(\frac{1}{2}\)
-
C.
-3
-
D.
1
Đáp án : A
Xét sự biến thiên và tìm các giá trị của y tại x khi y’ = 0, khi x với giá trị ở hai đầu mút.
Tập xác định \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
\(y' = \frac{{ - 5}}{{{{(x - 2)}^2}}} < 0,\forall x \in \left[ { - \frac{1}{2};1} \right]\)
\(y\left( { - \frac{1}{2}} \right) = 0,\) \(y\left( 1 \right) = - 3\).
Vậy giá trị lớn nhất của hàm số trên đoạn \([ - \frac{1}{2};1]\) bằng 0.
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ:
Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = {x^3} - 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} - 1\)
Đáp án : B
Quan sát bảng biến thiên, tìm đạo hàm, xét các điểm cực trị và các giá trị của hàm số tại điểm đó, thay số vào f(x), f’(x) để tìm các hệ số của phương trình.
Ta có: \(f'(x) = 3a{x^2} + 2bx + c\). Đồ thị đạt cực trị tại các điểm (0;1) và (-2;-3) nên f’(0) = 0, f’(-2) = 0.
Đồ thị hàm số đi qua các điểm (-2;-3) và (0;1) nên f(-2) = -3, f(0) = 1.
Ta có hệ phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{f'(0) = 0}\\{f(0) = 1}\\{f'( - 2) = 0}\\{f( - 2) = - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{12a - 4b = 0}\\{ - 8a + 4b + 1 = - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{a = - 1}\\{b = - 3}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^3} - 3{x^2} + 1\).
Công thức tính tích vô hướng của 2 vecto là?
-
A.
\(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow {a.} \overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
-
B.
\(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
-
C.
\(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
-
D.
\(\overrightarrow {a.} \overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right)\)
Đáp án : B
Dựa vào lý thuyết công thức tính tích vô hướng.
Công thức tính tích vô hướng của 2 vecto là: \(\overrightarrow {a.} \overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow {a,} \overrightarrow b } \right).\)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Xét các vecto \(\overrightarrow x = 2\overrightarrow a - \overrightarrow b \); \(\overrightarrow y = - 4\overrightarrow a + 2\overrightarrow b \); \(\overrightarrow z = - 3\overrightarrow b - 2\overrightarrow c \). Chọn khẳng định đúng?
-
A.
Hai vecto \(\overrightarrow y ,\overrightarrow z \) cùng phương
-
B.
Hai vecto \(\overrightarrow x ,\overrightarrow y \) cùng phương
-
C.
Hai vecto \(\overrightarrow x ,\overrightarrow z \) cùng phương
-
D.
Ba vecto \(\overrightarrow x ,\overrightarrow y ,\overrightarrow z \) đồng phẳng.
Đáp án : B
Sử dụng lí thuyết hai vecto cùng phương. \(\overrightarrow x \) cùng phương \(\overrightarrow y \) khi và chỉ khi \(\overrightarrow x = k\overrightarrow y \) với \(k \ne 0\).
Nhận thấy: \(\overrightarrow y = - 4\overrightarrow a + 2\overrightarrow b = - 2\left( {2\overrightarrow a + \overrightarrow b } \right) = - 2\overrightarrow x \) nên hai vecto \(\overrightarrow x ,\overrightarrow y \) cùng phương.
a) Hàm số f(x) đồng biến trên mỗi khoảng (-1;0) và (0;1)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng -3
d) Đồ thị hàm số không có đường tiệm cận
a) Hàm số f(x) đồng biến trên mỗi khoảng (-1;0) và (0;1)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng -3
d) Đồ thị hàm số không có đường tiệm cận
Quan sát đồ bảng biến thiên và nhận xét.
a) Sai. Hàm số f(x) nghịch biên trên (0;1) và đồng biến trên (-1;0).
b) Đúng. Số điểm cực trị của hàm số đã cho là 3 (x = -1, x = 0, x = 1).
c) Sai. Hàm số f(x) không có giá trị lớn nhất.
d) Đúng. Đồ thị hàm số liên tục trên và không có tiệm cận.
Cho hàm số \(y=x - \sqrt {{x^2} + 1} \).
a) Hàm số đã cho nghịch biến trên R
b) Đồ thị hàm số đã cho có cực tiểu
c) Đồ thị hàm số đã cho có 1 tiệm cận ngang
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
a) Hàm số đã cho nghịch biến trên R
b) Đồ thị hàm số đã cho có cực tiểu
c) Đồ thị hàm số đã cho có 1 tiệm cận ngang
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
Lập bảng biến thiên và nhận xét.
Tập xác định: \(D = \mathbb{R}\).
\(y' = 1 - \frac{x}{{\sqrt {{x^2} + 1} }} = \frac{{\sqrt {{x^2} + 1} - x}}{{\sqrt {{x^2} + 1} }} \).
Vì \(\sqrt {{x^2} + 1} > \sqrt {{x^2}} = \left| x \right| \Rightarrow \sqrt {{x^2} + 1} > x \Rightarrow \sqrt {{x^2} + 1} - x > 0\).
Mà \(\sqrt {{x^2} + 1} > 0\).
Vậy y’ > 0 với mọi x.
Ta có bảng biến thiên:
a) Sai. Hàm số đồng biến trên R.
b) Sai. Đồ thị hàm số đã cho không có cực tiểu.
c) Đúng. Đồ thị hàm số đã cho có tiệm cận ngang y = 0 vì \(\mathop {\lim }\limits_{x \to + \infty } y = 0\).
d) Đúng. Thay tọa độ x = 0, y = 0 của O(0;0) vào phương trình xem có thỏa mãn không:
\(0 = 0 - \sqrt {{0^2} + 1} \) (vô lí).
Vậy đồ thị hàm số không đi qua gốc tọa độ.
a) \(\overrightarrow {AB} = \overrightarrow {DC} \)
b) \(\overrightarrow {AC} = \overrightarrow {BD} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 2\overrightarrow {SO} \)
a) \(\overrightarrow {AB} = \overrightarrow {DC} \)
b) \(\overrightarrow {AC} = \overrightarrow {BD} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 2\overrightarrow {SO} \)
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc trung điểm, quy tắc trọng tâm.
a) Đúng. Vì hai vecto trên cùng hướng và cùng độ dài.
b) Sai. Vì hai vecto trên không cùng hướng.
c) Sai. Vì O là trung điểm của AC nên \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \).
d) Sai. Vì \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \).
Cho hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có \(AB = a\), \(BC = 2a\), \(A{A_1} = 3a\).
a) \(\left( {\overrightarrow {A{B_1}} ;\overrightarrow {{C_1}D} } \right) = {45^o}\)
b) \(\overrightarrow {{A_1}B} .\overrightarrow {{D_1}D} = 9{a^2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {{C_1}{A_1}} .\overrightarrow {{C_1}{B_1}} \)
d) \(\overrightarrow {{A_1}{D_1}} .\overrightarrow {{C_1}C} = 0\)
a) \(\left( {\overrightarrow {A{B_1}} ;\overrightarrow {{C_1}D} } \right) = {45^o}\)
b) \(\overrightarrow {{A_1}B} .\overrightarrow {{D_1}D} = 9{a^2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {{C_1}{A_1}} .\overrightarrow {{C_1}{B_1}} \)
d) \(\overrightarrow {{A_1}{D_1}} .\overrightarrow {{C_1}C} = 0\)
Sử dụng lý thuyết các vecto bằng nhau, các vecto đối nhau, góc giữa hai vecto.
a) Sai. Vì hai vecto trên ngược hướng nên \(\left( {\overrightarrow {A{B_1}} ;\overrightarrow {{C_1}D} } \right) = {180^o}\).
b) Đúng. \(\overrightarrow {{A_1}B} .\overrightarrow {{D_1}D} = \overrightarrow {{A_1}B} .\overrightarrow {{A_1}A} = \left| {\overrightarrow {{A_1}B} } \right|.\left| {\overrightarrow {{A_1}A} } \right|\cos \left( {\overrightarrow {{A_1}B} ,\overrightarrow {{A_1}A} } \right) = a\sqrt {10} .3a.\frac{{3a}}{{a\sqrt {10} }} = 9{a^2}\).
c) Đúng. \(\overrightarrow {AC} .\overrightarrow {AD} = - \overrightarrow {{C_1}{A_1}} .\left( { - \overrightarrow {{C_1}{B_1}} } \right) = \overrightarrow {{C_1}{A_1}} .\overrightarrow {{C_1}{B_1}} \).
d) Đúng. \(\overrightarrow {{A_1}{D_1}} .\overrightarrow {{C_1}C} = \overrightarrow {{A_1}{D_1}} .\overrightarrow {{D_1}D} = 0\) (vì \(\overrightarrow {{A_1}{D_1}} \) và \(\overrightarrow {{D_1}D} \) vuông góc với nhau).
Giá trị lớn nhất của hàm số \(y = x{(5 - 2x)^2}\) trên [0;3] là một phân số có dạng \(\frac{a}{b}\). Tính a + 2b.
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0
- Tìm giá trị lớn nhất điểm cực đại, cực tiểu của hàm số
Ta có: \(y' = 1{(5 - 2x)^2} + x.2(5 - 2x).(5 - 2x)' = 25 - 29x + 4{x^2} - 20x + 8{x^2} = 12{x^2} - 40x + 25\).
\(y' = 0\) khi \(x = \frac{5}{2}\) hoặc \(x = \frac{5}{6}\).
Ta có: \(y(0) = 0\); \(y\left( {\frac{5}{6}} \right) = \frac{{250}}{{27}}\); \(y\left( {\frac{5}{2}} \right) = 0\); \(y(3) = 3\).
Vậy giá trị lớn nhất của hàm số trên [0;3] là \(\frac{{250}}{{27}}\) khi \(x = \frac{5}{6}\).
Vậy \(a = 250,b = 27\). Khi đó \(a + 2b = 250 + 2.27 = 304.\)
Khoảng cách từ điểm A(-5;1) đến đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}}\) là bao nhiêu?
Đáp án:
Đáp án:
Tìm đường tiệm cận đứng của đồ thị bằng cách tìm giới hạn. Từ đó tính khoảng cách từ A đến tiệm cận.
Tập xác định: \(D = [ - 1;1]\backslash \{ 0\} \).
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}} = + \infty \), \(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}} = - \infty \).
Suy ra đường thẳng x = 0 (trục Oy) là đường tiệm cận đứng của đồ thị hàm số.
Vì hoành độ điểm A là -5 nên khoảng cách \(d(A,Oy) = \left| { - 5} \right| = 5\).
Trong không gian Oxyz, cho hình bình hành ABCD. Biết A(1;0;1), B(2;1;2), và D(1;-1;1). Tọa độ điểm C là (a;b;c). Tính tổng a + b + c.
Đáp án:
Đáp án:
Sử dụng quy tắc hình bình hành.
Vì ABCD là hình bình hành nên \(\overrightarrow {DC} = \overrightarrow {AB} \).
Ta có: \(\overrightarrow {DC} = (a - 1;b + 1c - 1)\) và \(\overrightarrow {AB} = (1;1;1)\).
Suy ra \(\left\{ {\begin{array}{*{20}{c}}{a - 1 = 1}\\{b + 1 = 1}\\{c - 1 = 1}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = 0}\\{c = 2}\end{array}} \right.\)
Vậy \(a = 2,b = 0,c = 2\). Khi đó \(a + b + c = 2 + 0 + 2 = 4\).
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G(x) = 0,025{x^2}(30 - x)\), trong đó x là liều lượng thuốc được tiêm cho bênh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án:
Đáp án:
Lập bảng biến thiên cho hàm số tính độ giảm huyết áp đó rồi tìm giá trị lớn nhất của hàm số đó.
Xét hàm số \(G(x) = 0,75{x^2} - 0,025{x^3};x \in (0; + \infty )\).
Ta có: \(G'(x) = 1,5x - 0,075{x^2} = 0 \Leftrightarrow \) x = 0 hoặc x = 20.
Bảng biến thiên:
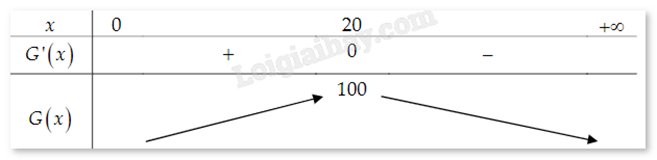
Từ bảng biến thiên, hàm G(x) đạt giá trị lớn nhất tại x = 20. Khi đó, độ giảm huyết áp là 100.
Một con nhện đang treo mình dưới một sợi tơ theo phương thẳng đứng thì bị một cơn gió thổi theo phương ngang làm dây treo lệch đi so với phương thẳng đứng một góc \({30^o}\). Biết trọng lượng của con nhện là P = 0,1 N. Xác định độ lớn của lực mà gió tác dụng lên con nhện ở vị trí cân bằng (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Tính lực F thông qua góc lượng giác.
Khi con nhện và sợi tơ cân bằng như hình dưới:
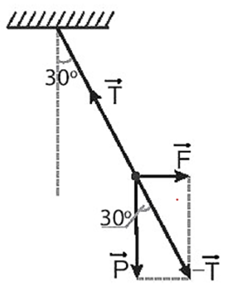
Ta có: \(\tan {30^o} = \frac{F}{P}\), suy ra \(F = P.\tan {30^o} = 0,1.\frac{1}{{\sqrt 3 }} \approx 0,06\) (N).
Hình vẽ dưới đây mô tả một sân cầu long với kích thước theo chuẩn quốc tế. Ta chọn hệ trục Oxyz cho sân đó như hình vẽ (đơn vị trên mỗi trục là mét). Giả sử AB là một trụ cầu lông để căng lưới. Gọi (x;y;z) là tọa độ của \(\overrightarrow {AB} \). Tính x + y + x.
Đáp án:
Đáp án:
Tìm tọa độ của A, B bằng cách quan sát hình vẽ, từ đó tính tọa độ \(\overrightarrow {AB} \).
Quan sát hình vẽ, thấy điểm A có tọa độ \(\left( {6,1;\frac{{13,4}}{2};0} \right) = \left( {6,1;6,7;0} \right)\).
Điểm B có tọa độ \(\left( {6,1;\frac{{13,4}}{2};1,55} \right) = \left( {6,1;6,7;1,55} \right)\).
Suy ra \(\overrightarrow {AB} = (0;0;1,55)\).
Vậy x + y + z = 0 + 0 + 1,55 = 1,55.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) xác định trên R{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây sai?
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
