Đề thi giữa kì 1 Toán 12 - Đề số 10
Đề thi giữa kì 1 Toán 12 - Đề số 10
Đề bài
-
A.
\(\left( { - \infty ;2} \right)\)
-
B.
\(\left( {2; + \infty } \right)\)
-
C.
\(\left( { 0;2} \right)\)
-
D.
\(\left( { - \infty ;0} \right)\)
Hàm số nào dưới đây đồng biến trên khoảng \(( - \infty ; + \infty )\)?
-
A.
\(y = - {x^3} - 2x + 1\)
-
B.
\(y = \frac{{x - 2}}{{x + 1}}\)
-
C.
\(y = 3{x^3} + 3x - 2\)
-
D.
\(y = 2{x^3} - 5x + 1\)
-
A.
-2
-
B.
-3
-
C.
3
-
D.
2
Cho hàm số y = f(x) có đạo hàm \(f'(x) = ({x^2} - 4)(x + 2)(x - 3)\) và liên tục trên \(\mathbb{R}\). Số điểm cực trị của hàm số đã cho là
-
A.
5
-
B.
2
-
C.
3
-
D.
1
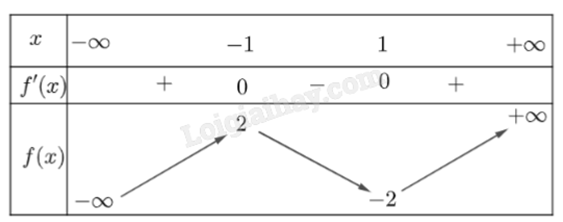
Cho hàm số y = f(x) có bảng biến thiên như hình. Giá trị nhỏ nhất của hàm số y = f(x) trên [-1;1] bằng
-
A.
-3
-
B.
-1
-
C.
-2
-
D.
1
Giá trị lớn nhất của hàm số \(\frac{{2x + 1}}{{x - 2}}\) trên đoạn \([ - \frac{1}{2};1]\) bằng:
-
A.
0
-
B.
\(\frac{1}{2}\)
-
C.
-3
-
D.
1
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\backslash \{ 1\} \) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f(x) là

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Số đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt {{x^2} - 4x + 3} }}{{{x^2} - 4}}\) là
-
A.
1
-
B.
2
-
C.
3
-
D.
4
-
A.
\(f(x) = {x^3} + 3x + 1\)
-
B.
\(f(x) = {x^3} - 3x - 1\)
-
C.
\(f(x) = {x^3} - 3x + 1\)
-
D.
\(f(x) = - {x^3} - 3x + 1\)
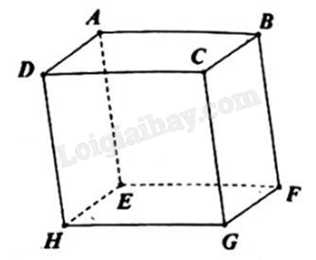
Cho hình hộp ABCD.EFGH (minh họa như hình bên). Vecto nào sau đây bằng vecto \(\overrightarrow {FH} \)?
-
A.
\(\overrightarrow {BD} \)
-
B.
\(\overrightarrow {DB} \)
-
C.
\(\overrightarrow {BA} \)
-
D.
\(\overrightarrow {AB} \)
-
A.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{C^{\prime}B^{\prime}}$.
-
B.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC}$.
-
C.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC^{\prime}}$.
-
D.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{A^{\prime}A}$.
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
-
A.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{C^{\prime}B^{\prime}}$.
-
B.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC}$.
-
C.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC^{\prime}}$.
-
D.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{A^{\prime}A}$.
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
Cho hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\)có đồ thị như hình vẽ.
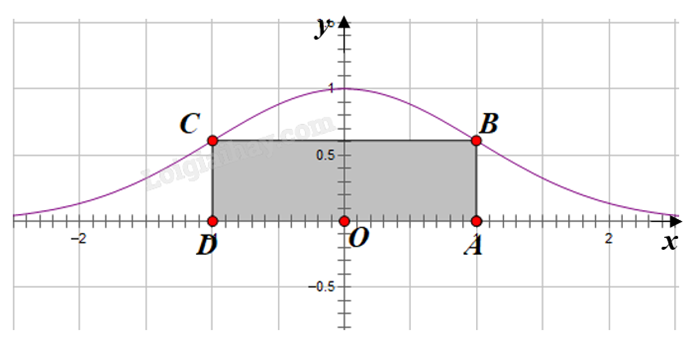
Biết ABCD là hình chữ nhật thay đổi sao cho hai điểm B, C luôn thuộc đồ thị hàm số đã cho. Hai điểm A, D nằm trên trục hoành (điểm A thuộc tia Ox).
a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.
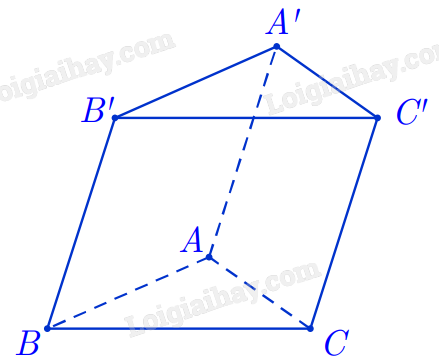
Cho hình chóp tứ giác đều $S.ABCD$ có độ dài tất cả các cạnh đều bằng $a$. Đáy $ABCD$ có tâm là $O$.
Các mệnh đề sau đúng hay sai?
a) $\overset{\rightarrow}{OA} + \overset{\rightarrow}{OB} + \overset{\rightarrow}{OC} + \overset{\rightarrow}{OD} = 4\overset{\rightarrow}{SO}$.
b) $\overset{\rightarrow}{SA} + \overset{\rightarrow}{SC} = \overset{\rightarrow}{SB} + \overset{\rightarrow}{SD}$.
c) $\left( {\overset{\rightarrow}{SA},\,\overset{\rightarrow}{AC}} \right) = 45{^\circ}$.
d) $\overset{\rightarrow}{SA} \cdot \overset{\rightarrow}{AC} = - a^{2}$.
Lời giải và đáp án
-
A.
\(\left( { - \infty ;2} \right)\)
-
B.
\(\left( {2; + \infty } \right)\)
-
C.
\(\left( { 0;2} \right)\)
-
D.
\(\left( { - \infty ;0} \right)\)
Đáp án : C
Hàm số nghịch biến trên khoảng đồ thị đi xuống từ trái sang phải.
Quan sát đồ thị, ta thấy đồ thị đi xuống từ trái sang trong khoảng \(\left( { 0;2} \right)\) nên hàm số nghịch biến trên khoảng đó.
Hàm số nào dưới đây đồng biến trên khoảng \(( - \infty ; + \infty )\)?
-
A.
\(y = - {x^3} - 2x + 1\)
-
B.
\(y = \frac{{x - 2}}{{x + 1}}\)
-
C.
\(y = 3{x^3} + 3x - 2\)
-
D.
\(y = 2{x^3} - 5x + 1\)
Đáp án : C
Tính đạo hàm của từng hàm số rồi xét sự biến thiên.
Xét đáp án A: \(y' = - 3{x^2} - 2 < 0\), \(\forall x \in \mathbb{R}\) nên hàm số nghịch biến trên \(\mathbb{R}\). Loại A.
Xét đáp án B: Hàm số không liên tục trên \(\mathbb{R}\). Loại B.
Xét đáp án C: \(y' = 9{x^2} + 3 > 0\), \(\forall x \in \mathbb{R}\) nên hàm số đồng biến trên \(\mathbb{R}\). Chọn C.
Xét đáp án D: \(y' = 6{x^2} - 5 = 0 \Leftrightarrow \pm \frac{{\sqrt {30} }}{6}\) nên hàm số không đồng biến trên \(\mathbb{R}\). Loại D.
-
A.
-2
-
B.
-3
-
C.
3
-
D.
2
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Giá trị cực đại của hàm số đã cho bằng 2.
Cho hàm số y = f(x) có đạo hàm \(f'(x) = ({x^2} - 4)(x + 2)(x - 3)\) và liên tục trên \(\mathbb{R}\). Số điểm cực trị của hàm số đã cho là
-
A.
5
-
B.
2
-
C.
3
-
D.
1
Đáp án : B
Lập bảng biến thiên và xét dấu.
Ta có bảng xét dấu:

Vậy f(x) có hai điểm cực trị là x = 2 và x = 3.
Cho hàm số y = f(x) có bảng biến thiên như hình. Giá trị nhỏ nhất của hàm số y = f(x) trên [-1;1] bằng

-
A.
-3
-
B.
-1
-
C.
-2
-
D.
1
Đáp án : C
Quan sát bảng biến thiên và nhận xét.
Quan sát bảng biến thiên, thấy \(f(x) \ge - 2\) với mọi x thuộc [-1;1].
Vậy giá trị nhỏ nhất của f(x) trên [-1;1] là -2.
Giá trị lớn nhất của hàm số \(\frac{{2x + 1}}{{x - 2}}\) trên đoạn \([ - \frac{1}{2};1]\) bằng:
-
A.
0
-
B.
\(\frac{1}{2}\)
-
C.
-3
-
D.
1
Đáp án : A
Bước 1: Tìm tập xác định (trong trường hợp xét trên đoạn [a;b], tập xác định đang xét chính là đoạn đó).
Bước 2: Tính đạo hàm f’(x). Tìm các giá trị thuộc đoạn [a;b] mà tại đó f’(x) = 0 hoặc f’(x) không tồn tại. (Các điểm này còn được gọi là điểm cực trị hoặc điểm dừng nếu đạo hàm bằng 0, hoặc điểm kì dị nếu đạo hàm không tồn tại).
Bước 3: Tính giá trị của hàm số tại các điểm vừa tìm được ở Bước 2 và tại hai đầu mút của đoạn [a;b]. Tức là tính các giá trị .
Giá trị lớn nhất trong số các giá trị vừa tính chính là GTLN của hàm số trên đoạn [a;b].
Giá trị nhỏ nhất trong số các giá trị vừa tính chính là GTNN của hàm số trên đoạn [a;b].
Tập xác định \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
\(y' = \frac{{ - 5}}{{{{(x - 2)}^2}}} < 0,\forall x \in \left[ { - \frac{1}{2};1} \right]\)
\(y\left( { - \frac{1}{2}} \right) = 0,\) \(y\left( 1 \right) = - 3\).
Vậy giá trị lớn nhất của hàm số trên đoạn \([ - \frac{1}{2};1]\) bằng 0.
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\backslash \{ 1\} \) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f(x) là

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Ta có $\lim_{x \to 1^+} y = -\infty$; $\lim_{x \to 1^-} x = +\infty $ nên ta có một tiệm cận đứng là $x=1$.
Mặt khác $\lim_{x \to +\infty} y = -1$; $\lim_{x \to -\infty} y = 1 $ nên ta có hai tiệm cận ngang là $y=1$ và $y=-1$.
Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.
Số đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt {{x^2} - 4x + 3} }}{{{x^2} - 4}}\) là
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } f(x) = {y_0}\).
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = {\rm{\;}} + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = {\rm{\;}} - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = {\rm{\;}} + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = {\rm{\;}} - \infty \).
Tiệm cận ngang:
TXĐ: \(D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\backslash \left\{ { - 2} \right\}\)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} - 4x + 3} }}{{{x^2} - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} }}{{x\left( {x - \frac{4}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} }}{{x - \frac{4}{x}}}\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \sqrt {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} = \sqrt 1 = 1\) và \(\mathop {\lim }\limits_{x \to + \infty } \left( {x - \frac{4}{x}} \right) = + \infty \) suy ra \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} }}{{x - \frac{4}{x}}} = 0\).
Vậy đồ thị có tiệm cận ngang là y = 0.
Tiệm cận đứng:
Vì \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} - 4x + 3} }}{{{x^2} - 4}}\) không xác định nên x = 2 không phải tiệm cận đứng.
Vì \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{\sqrt {{x^2} - 4x + 3} }}{{{x^2} - 4}} = - \infty \) và \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{\sqrt {{x^2} - 4x + 3} }}{{{x^2} - 4}} = + \infty \) nên x = -2 là tiệm cận đứng.
Vậy đồ thị có tiệm cận đứng là x = -2.
-
A.
\(f(x) = {x^3} + 3x + 1\)
-
B.
\(f(x) = {x^3} - 3x - 1\)
-
C.
\(f(x) = {x^3} - 3x + 1\)
-
D.
\(f(x) = - {x^3} - 3x + 1\)
Đáp án : C
Quan sát đồ thị và nhận xét. Sử dụng phương pháp loại trừ.
Hàm số có dạng \(y = f(x) = a{x^3} + bx + c\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) nên a > 0. Loại D.
Đồ thị cắt trục tung tại điểm có tung độ dương nên c > 0. Loại B.
Xét đáp án A: \(f'(x) = 3{x^2} + 3 = 0 \Leftrightarrow {x^2} = - 1\) (vô lí) nên hàm số \(f(x) = {x^3} + 3x + 1\) không có cực trị. Loại A.
Cho hình hộp ABCD.EFGH (minh họa như hình bên). Vecto nào sau đây bằng vecto \(\overrightarrow {FH} \)?

-
A.
\(\overrightarrow {BD} \)
-
B.
\(\overrightarrow {DB} \)
-
C.
\(\overrightarrow {BA} \)
-
D.
\(\overrightarrow {AB} \)
Đáp án : A
Hai vecto bằng nhau nếu chúng cùng hướng và có độ dài bằng nhau.
\(\overrightarrow {FH} = \overrightarrow {BD} \) vì chúng cùng hướng và FH = BD.
-
A.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{C^{\prime}B^{\prime}}$.
-
B.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC}$.
-
C.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC^{\prime}}$.
-
D.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{A^{\prime}A}$.
Đáp án : B
Áp dụng quy tắc ba điểm.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BA} + \overset{\rightarrow}{AC} = \overset{\rightarrow}{BC}$.
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
Đáp án : C
Đưa về hai vecto chung gốc để xác định góc.
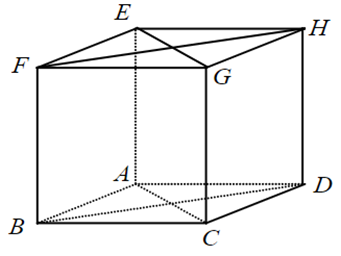
Ta có: EG//AC (do ACGE là hình bình hành), suy ra \(\left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^o}\).
-
A.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{C^{\prime}B^{\prime}}$.
-
B.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC}$.
-
C.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC^{\prime}}$.
-
D.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{A^{\prime}A}$.
Đáp án : B
Áp dụng quy tắc ba điểm.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BA} + \overset{\rightarrow}{AC} = \overset{\rightarrow}{BC}$.
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
Đáp án : C
Đưa về hai vecto chung gốc để xác định góc.

Ta có: EG//AC (do ACGE là hình bình hành), suy ra \(\left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^o}\).
Cho hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\)có đồ thị như hình vẽ.

Biết ABCD là hình chữ nhật thay đổi sao cho hai điểm B, C luôn thuộc đồ thị hàm số đã cho. Hai điểm A, D nằm trên trục hoành (điểm A thuộc tia Ox).
a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.
a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.
Tìm tập xác định, tính đạo hàm rồi lập bảng biến thiên, tìm giá trị lớn nhất.
a) Đúng. Hàm số mũ \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Sai. Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y'\, = {\left( { - \frac{1}{2}{x^2}} \right)^\prime }{e^{ - \frac{1}{2}{x^2}}} = - x{e^{ - \frac{1}{2}{x^2}}}\).
c) Sai. Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với x > 0 thì cạnh AD = 2x, cạnh \(AB = {e^{ - \frac{1}{2}{x^2}}}\).
Diện tích hình chữ nhật ABCD được tính theo công thức \(S\left( x \right) = 2x{e^{ - \frac{1}{2}{x^2}}}\).
d) Đúng. Xét hàm số \(S\left( x \right) = 2x{e^{ - \frac{1}{2}{x^2}}}\) trên khoảng \(\left( {0; + \infty } \right)\).
\(S'\left( x \right) = 2{e^{ - \frac{1}{2}{x^2}}} - 2{x^2}{e^{ - \frac{1}{2}{x^2}}} = 2{e^{ - \frac{1}{2}{x^2}}}\left( {1 - {x^2}} \right) = 0 \Leftrightarrow 1 - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\).
Bảng biến thiên:
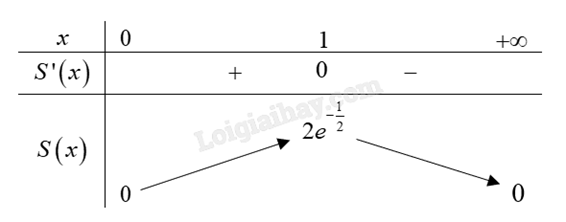
Hàm số S(x) đạt giá trị lớn nhất khi x = 1. Khi đó AD = 2.
Cho hình chóp tứ giác đều $S.ABCD$ có độ dài tất cả các cạnh đều bằng $a$. Đáy $ABCD$ có tâm là $O$.
Các mệnh đề sau đúng hay sai?
a) $\overset{\rightarrow}{OA} + \overset{\rightarrow}{OB} + \overset{\rightarrow}{OC} + \overset{\rightarrow}{OD} = 4\overset{\rightarrow}{SO}$.
b) $\overset{\rightarrow}{SA} + \overset{\rightarrow}{SC} = \overset{\rightarrow}{SB} + \overset{\rightarrow}{SD}$.
c) $\left( {\overset{\rightarrow}{SA},\,\overset{\rightarrow}{AC}} \right) = 45{^\circ}$.
d) $\overset{\rightarrow}{SA} \cdot \overset{\rightarrow}{AC} = - a^{2}$.
a) $\overset{\rightarrow}{OA} + \overset{\rightarrow}{OB} + \overset{\rightarrow}{OC} + \overset{\rightarrow}{OD} = 4\overset{\rightarrow}{SO}$.
b) $\overset{\rightarrow}{SA} + \overset{\rightarrow}{SC} = \overset{\rightarrow}{SB} + \overset{\rightarrow}{SD}$.
c) $\left( {\overset{\rightarrow}{SA},\,\overset{\rightarrow}{AC}} \right) = 45{^\circ}$.
d) $\overset{\rightarrow}{SA} \cdot \overset{\rightarrow}{AC} = - a^{2}$.
Áp dụng tính chất trung điểm và tích vô hướng của hai vecto.

a) Sai. Vì \(S.ABCD\) là hình chóp tứ giác đều nên đáy \(ABCD\) là hình vuông.
Suy ra tâm \(O\) là trung điểm của các đường chéo \(AC\) và \(BD\).
Do đó, \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) và \(\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \).
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
b) Đúng. Với điểm \(S\), ta có: \(\left\{ \begin{array}{l}\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \\\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \end{array} \right.\).
Suy ra \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
c) Sai. Tứ giác \(ABCD\) là hình vuông có độ dài mỗi cạnh là \(a\) nên độ dài đường chéo \(AC\) là \(a\sqrt 2 \). Tam giác \(SAC\) có \(SA = SC = a\) và \(AC = a\sqrt 2 \) nên tam giác \(SAC\) vuông cân tại \(S\), suy ra \(\widehat {SAC} = 45^\circ \). Do đó, \(\left( {\overrightarrow {SC} ,\,\overrightarrow {AC} } \right) = 180^\circ - \widehat {SAC} = 180^\circ - 45^\circ = 135^\circ \).
d) Đúng. \(\overrightarrow {SA} \cdot \overrightarrow {AC} = \left| {\overrightarrow {SA} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot \cos 135^\circ = a \cdot a\sqrt 2 \cdot \left( { - \frac{{\sqrt 2 }}{2}} \right) = - {a^2}\).
a) Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số.
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số.
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ (nếu có và dễ tìm),...
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
b) Quan sát đồ thị và tìm khoảng cách giữa 2 cực trị. Dùng định lí Pytago để tìm khoảng cách đó.
a) Tập xác định: \(D = \mathbb{R}\).
- Chiều biến thiên:
\(y' = {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Trên các khoảng (\( - \infty \); 0), (2; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (0; 2) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
- Cực trị:
Hàm số đạt cực đại tại x = 0 và \({y_{cd}} = 4\).
Hàm số đạt cực tiểu tại x = 2 và \({y_{ct}} = \frac{8}{3}\).
- Các giới hạn tại vô cực:
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (\frac{1}{3}{x^3} - {x^2} + 4) = - \infty \);
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (\frac{1}{3}{x^3} - {x^2} + 4) = + \infty \).
- Bảng biến thiên:
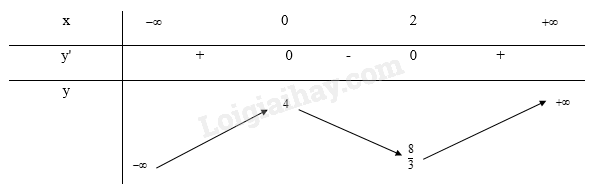
Khi x = 0 thì y = 4 nên (0; 4) là giao điểm của đồ thị với trục Oy.
Ta có: \(y = 0 \Leftrightarrow \frac{1}{3}{x^3} - {x^2} + 4 = 0 \Leftrightarrow x = - 1,61\).
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-1,61; 0).
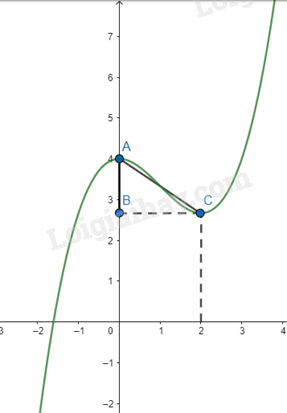
b) Khoảng cách giữa 2 cực trị là \(AC = \sqrt {{{(2 - 0)}^2} + {{\left( {\frac{8}{3} - 4} \right)}^2}} = \frac{{2\sqrt {13} }}{3}\).
Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}\).
Xét \(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \frac{{20}}{{x + 3}} = 0\).
Vậy đường thẳng \(y = x - 6\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).
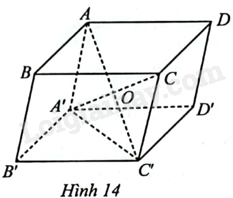
Sử dụng quy tắc hình hộp.
a) Theo quy tắc hình hộp ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Do đó \(\left| {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right| = \left| {\overrightarrow {AC'} } \right| = AC' = 2AO = 2{\rm{a}}\).
b) Theo quy tắc hình hộp ta có: \(\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} = \overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {C'C} = \overrightarrow {C'A} \).
Do đó \(\left| {\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} } \right| = \left| {\overrightarrow {C'A} } \right| = C'A = 2AO = 2{\rm{a}}\).
Đề thi giữa kì 1 Toán 12 - Đề số 9
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây sai?
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) xác định trên R{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:











Danh sách bình luận