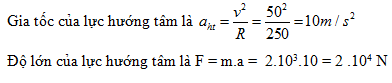50 bài tập Lực hướng tâm mức độ vận dụng

Câu hỏi 1 :

Chọn câu trả lời đúng khi nói về lực tác dụng lên vật chuyển động tròn đều ?

A Ngoàicác lực cơ học, vật còn chịu thêm tác dụng của lực hướng tâm
B Hợp lực của tất cả các lực tác dụng lên vật đóng vai trò là lực hướng tâm
C Vật không chịu tác dụng của lực nào ngoài lực hướng tâm
D Hợp lực của tất cả các lực tác dụng lên vật nằm theo phương tiếp tuyến với quỹ đạo tại điểm khảo sát

Đáp án: B

Lời giải chi tiết:

Đáp án B

Đáp án - Lời giải

Câu hỏi 2 :

Khi nói về chuyển động tròn của một vật, câu nào sau đây là sai ?

A Lực quán tính li tâm và lực hướng tâm ngược chiều nhau
B Lực quán tính li tâm và lực hướng tâm có cùng giá và cùng độ lớn như nhau
C Nếu coi lực quán tính li tâm là lực tác dụng thì lực hướng tâm là phản lực và ngược lại
D Lực quán tính li tâm và lực hướng tâm là hai cân bằng nhau

Đáp án: C

Lời giải chi tiết:

Đáp án C

Đáp án - Lời giải

Câu hỏi 3 :

Trong các phát biểu sau, phát biểu nào SAI:

A Khi vật chuyển động tròn đều, hợp lực tác dụng lên vật bằng 0.
B Khi vật chuyển động tròn đều, hợp lực tác dụng lên vật có hướng hướng vào tâm.
C Khi vật chuyển động thẳng đều, hợp lực tác dụng lên vật bằng 0.
D Lực hướng tâm không phải là một loại lực trong tự nhiên.

Đáp án: A

Lời giải chi tiết:

Đáp án A

Đáp án - Lời giải

Câu hỏi 4 :

Một ôtô có khối lượng 1200kg chuyển động đều qua một đoạn cầu vượt (coi là cung tròn) với tốc độ có độ lớn là 36km/h. Biết bán kính cong của đoạn cầu vượt là 50m. Lấy g = 10m/s². Áp lực của ôtô vào mặt đường tại điểm cao nhất theo đơn vị kN :

A 119,5
B 117,6
C 14,4
D 9,6

Đáp án: D

Lời giải chi tiết:

Đáp án D

Đáp án - Lời giải

Câu hỏi 5 :

Một vật khối lượng m đặt trên đĩa quay đều với vận tốc góc w . Vật đã vạch nên đường tròn bán kính R. Vật đã chuyển động tròn nên lực đóng vai trò lực hứơng tâm là:

A Trọng lực
B Phản lực của đĩa
C Lực ma sát nghỉ
D Hợp lực của 3 lực trên.

Đáp án: D

Đáp án - Lời giải

Câu hỏi 6 :

Ở những đoạn đường vòng, mặt đường được nâng lên một bên. Việc làm này nhằm mục đích nào kể sau đây?

A Giới hạn vận tốc của xe
B Tạo lực hướng tâm
C Tăng lực ma sát
D Cho nước mưa thoát dễ dàng.

Đáp án: B

Lời giải chi tiết:

Ở những đoạn đường vòng, mặt đường được nâng lên một bên. Việc làm này nhằm mục đích tạo lực hướng tâm

Đáp án - Lời giải

Câu hỏi 7 :

Một xe đua chạy quanh một đường tròn nằm ngang, bán kính 250m. Vận tốc xe không đổi có độ lớn là 50m/s. Khối lượng xe là 2.10³ kg . Lực hướng tâm tác dụng lên xe lúc này là

A lực đẩy của động cơ
B lực hãm
C lực ma sát
D lực của vô – lăng ( tay lái )

Đáp án: C

Đáp án - Lời giải

Câu hỏi 8 :

Một vật nặng 4,0kg được gắn vào một dây thừng dài 2m. Nếu vật đó quay tự do thành một vòng tròn quanh trục thẳng đứng gắn với đầu dây thì sức căng của dây là bao nhiêu khi căng tối đa và vật có vận tốc 5m/s ?

A 5,4N
B 10,8N
C 21,6N
D 50N

Đáp án: D

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 9 :

Một xe đua chạy quanh một đường tròn nằm ngang, bán kính 250m. Vận tốc xe không đổi có độ lớn là 50m/s. Khối lượng xe là 2.10³ kg. Độ lớn của lực hướng tâm của chiếc xe là:

A 10 N
B 4 .10² N
C 4 . 10³ N
D 2 .10⁴ N

Đáp án: D

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 10 :

Gọi m là khối lượng của vật chuyển động tròn đều, v là tốc độ dài của vật, r là bán kính của quỹ đạo tròn. Biểu thức xác định độ lớn lực hướng tâm có dạng

A
\[{\user2{F}_{\user2{ht}}} = \frac{{\user2{m}{\user2{v}^\user2{2}}}}{{{\user2{r}^\user2{2}}}}\user2{.}\]
B

\[{\user2{F}_{\user2{ht}}} = \frac{{\user2{m}{\user2{r}^\user2{2}}}}{\user2{v}}\user2{.}\]
C
\[{\user2{F}_{\user2{ht}}} = \frac{{\user2{m}{\user2{v}^\user2{2}}}}{{{\user2{r}^{}}}}\user2{.}\]
D
\[{\user2{F}_{\user2{ht}}} = \frac{{\user2{m}{\user2{v}^\user2{2}}}}{{\user2{2}{\user2{r}^{}}}}\user2{.}\]

Đáp án: C

Phương pháp giải:

Công thức tính lực hướng tâm

Lời giải chi tiết:

Công thức tính lực hướng tâm là

\({\user2{F}_{\user2{ht}}} = \frac{{\user2{m}{\user2{v}^\user2{2}}}}{{{\user2{r}^{}}}}\user2{.}\)

Đáp án - Lời giải

Câu hỏi 11 :

Một ô tô có khối lượng 1,5 tấn chuyển động đều qua một đoạn cầu vượt (coi là cung tròn) với tốc độ 54 km/h. Hỏi áp lực của ô tô vào mặt đường tại điểm cao nhất bằng bao nhiêu? Biết bán kính cong của đoạn cầu vượt là 100 m. Lấy g = 10 m/s².

A 11 625 N.
B 3375 N
C 18375 N.
D 15000 N.

Đáp án: A

Phương pháp giải:

- Lực hướng tâm: \({F_{ht}} = m{a_{ht}} = \frac{{m{v^2}}}{R}\)

- Áp dụng định luật II Niu - tơn.

Lời giải chi tiết:

Đáp án A

Ta có: v = 54km/h = 15m/s; R = 50m; m = 1500kg; \(g = 10m/{s^2}\)

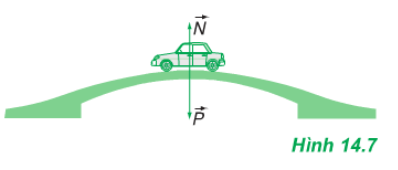
Khi ô tô chuyển động đến điểm cao nhất, các lực tác dụng lên xe được biểu diễn như hình vẽ:

Áp dụng đinh luật II Niu - tơn ta có: \(\vec P + \vec N = m\overrightarrow {{a_{ht}}} (*)\)

Chọn chiều dương hướng vào tâm, chiếu phương trình (*) lên phương bán kính ta được:

\(P - N = \frac{{m{v^2}}}{R} \Rightarrow N = P - \frac{{m{v^2}}}{R} = mg - \frac{{m{v^2}}}{R}{\rm{ }} \Rightarrow N = 1500.10 - \frac{{{{1500.15}^2}}}{{100}} = 11625N{\rm{ }}\)

Đáp án - Lời giải

Câu hỏi 12 :

Ở những đoạn đường vòng, mặt đường được nâng lên một bên. Việc làm này nhằm mục đích:

A tăng lực ma sát.
B giới hạn vận tốc của xe.
C tạo lực hướng tâm nhờ phản lực của đường.
D giảm lực ma sát.

Đáp án: C

Lời giải chi tiết:

Đáp án C

Đáp án - Lời giải

Câu hỏi 13 :

Một vật có khối lượng 300g chuyển động tròn đều trong thời gian 1 phút đi được 120 vòng. Biết bán kính của quỹ đạo tròn là 10cm. Tìm lực hướng tâm tác dụng lên vật trong quá trình chuyển động?

Phương pháp giải:

Áp dụng các công thức trong chuyển động tròn đều

Lời giải chi tiết:

Chu kỳ chuyển động: T = 0,5s suy ra ω = 4π (rad/s)

R = 10cm = 0,1m, m = 300g = 0,3kg

Lực hướng tâm: F_ht = ma_ht = mRω² = 4,8N

Đáp án - Lời giải

Câu hỏi 14 :

a) Viết công thức của lực hướng tâm.
b) Cột dây vào một đùm chìa khóa rồi quay cho nó chuyển động tròn đều quanh ngón tay trỏ, lực nào đóng vai trò là lực hướng tâm giữ vật. Tính độ lớn lực hướng tâm đó biết chùm chìa khóa có khối lượng 50g, bá n kính quỹ đạo là 0,5m và tốc độ góc của vật là 10rad/s

A a. \({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r\)

b. F = 2,5N
B a. \({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r\)

b. F = 22,5N
C a. \({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}\)

b. F = 2,5N
D a. \({F_{ht}} = m.{a_{ht}} = m.{\omega}.r\)

b. F = 2,5N

Đáp án: A

Phương pháp giải:

Áp dụng công thức tính lực hướng tâm :

\({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r\)

Lời giải chi tiết:

a) công thức tính lực hướng tâm :

\({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r\)

b)

Lực đóng vai trò lực hướng tâm trong chuyển động của chìa khóa là lực căng dây T, giúp vật không bị văng ra xa.

Áp dụng công thức tính lực hướng tâm :

\({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r = 0,{05.10^2}.0,5 = 2,5N\)

Đáp án - Lời giải

Câu hỏi 15 :

Một vệ tinh nhân tạo có khối lượng m chuyển động tròn đều quanh Trái Đất ở độ cao h= 1600 km. Trái Đất có khối lượng là M = 6.10²⁴ kg và bán kính R= 6400km. Cho hằng số hấp dẫn là G=6,67.10-11Nm² /kg² .

a. Hãy tính vận tốc chuyển động của vệ tinh trên quỹ đạo.

b. Tính chu kỳ chuyển động của vệ tinh.

A a. 707284m/s

b. 710683s
B a. 7072,84m/s

b. 71068,3s
C a. 70,7284m/s

b. 7106,83s
D a. 7072,84m/s

b. 7106,83s

Đáp án: D

Phương pháp giải:

a) Lực đóng vai trò lực hướng tâm giữ vệ tinh chuyển động tròn đều quanh Trái đất chính là lực hấp dẫn giữa Trái Đất và vệ tinh

\({F_{hd}} = G.\frac{{m.M}}{{{{(R + h)}^2}}}\)

. còn lực hướng tâm có liên hệ với vận tốc dài (vận tốc chuyển động của vệ tinh)

\({F_{ht}} = m.{a_{ht}} = m.\frac{{{v^2}}}{R}\)

b) Chu kì chuyển động của vệ tinh là thời gian nó đi hết 1 vòng quanh Trái Đất

\(v = r.\omega = r.\frac{{2\pi }}{T} \Rightarrow T = \frac{{2\pi r}}{v}\)

Lời giải chi tiết:

a) Lực đóng vai trò lực hướng tâm giữ vệ tinh chuyển động tròn đều quanh Trái đất chính là lực hấp dẫn giữa Trái Đất và vệ tinh.

\({F_{hd}} = G.\frac{{m.M}}{{{{(R + h)}^2}}}\) = \({F_{ht}} = m.{a_{ht}} = m.\frac{{{v^2}}}{R}\)

Vậy ta có

\(\begin{array}{l}
G.\frac{{m.M}}{{{{(R + h)}^2}}} = \frac{{m.{v^2}}}{{(R + h)}}\\
\Leftrightarrow 6,{67.10^{ - 11}}.\frac{{m{{.6.10}^{24}}}}{{{{(6400000 + 1600000)}^2}}} = \frac{{m.{v^2}}}{{6400000 + 1600000}}\\
\Leftrightarrow v = 7072,84m/s
\end{array}\)

b) Áp dụng công thức

\(v = r.\omega = r.\frac{{2\pi }}{T} \Rightarrow T = \frac{{2\pi (R + h)}}{v} = \frac{{2.\pi .(6400000 + 1600000)}}{{7072,84}} = 7106,83s\)

Đáp án - Lời giải

Câu hỏi 16 :

Nêu định nghĩa lực hướng tâm, viết công thức.

Áp dụng : Một xe có khối lượng 120 kg đi quanh vòng xoay với tốc độ không đổi 4 m/s. Tính độ lớn lực hướng tâm tác dụng lên xe ? Biết bán kính vòng xoay bằng 10m.

A - Định nghĩa lực hướng tâm: Lực (hay hợp lực) tác dụng vào một vật chuyển động tròn đều và gât ra cho vật gia tốc hướng tâm gọi là lực hướng tâm).

- Công thức: \({{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}r=\frac{m{{v}^{2}}}{r}\)

- Áp dụng: 192N
B - Định nghĩa lực hướng tâm: Lực (hay hợp lực) tác dụng vào một vật chuyển động tròn đều và gât ra cho vật gia tốc hướng tâm gọi là lực hướng tâm).

- Công thức: \({{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}r=\frac{m{{v}^{2}}}{r}\)

- Áp dụng: 102N
C - Định nghĩa lực hướng tâm: Lực (hay hợp lực) tác dụng vào một vật chuyển động tròn đều và gât ra cho vật gia tốc hướng tâm gọi là lực hướng tâm).

- Công thức: \({{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}r=\frac{m{{v}^{2}}}{r}\)

- Áp dụng: 210N
D - Định nghĩa lực hướng tâm: Lực (hay hợp lực) tác dụng vào một vật chuyển động tròn đều và gât ra cho vật gia tốc hướng tâm gọi là lực hướng tâm).

- Công thức: \({{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}r=\frac{m{{v}^{2}}}{r}\)

- Áp dụng: 112N

Đáp án: A

Phương pháp giải:

- Định nghĩa lực hướng tâm: Lực (hay hợp lực) tác dụng vào một vật chuyển động tròn đều và gât ra cho vật gia tốc hướng tâm gọi là lực hướng tâm).

- Công thức: \({{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}r=\frac{m{{v}^{2}}}{r}\)

Lời giải chi tiết:

- Định nghĩa lực hướng tâm: Lực (hay hợp lực) tác dụng vào một vật chuyển động tròn đều và gât ra cho vật gia tốc hướng tâm gọi là lực hướng tâm).

- Công thức: \({{F}_{ht}}=m{{a}_{ht}}=m{{\omega }^{2}}r=\frac{m{{v}^{2}}}{r}\)

Áp dụng:

Độ lớn lực hướng tâm: \({{F}_{ht}}=\frac{m{{v}^{2}}}{r}=\frac{{{120.4}^{2}}}{10}=192N\)

Đáp án - Lời giải

Câu hỏi 17 :

Một vật có khối lượng 2 kg chuyển động tròn đều với tốc độ góc 2 rad/s. Biết bán kính quỹ đạo là R = 5m. Hãy tính lực hướng tâm tác dụng lên vật.

A 40N
B 50N
C 60N
D 70N

Đáp án: A

Phương pháp giải:

- Gia tốc hướng tâm: \({{a}_{ht}}=mr{{\omega }^{2}}=\frac{m{{v}^{2}}}{r}\)

- Lực hướng tâm: F_ht = ma_ht

Lời giải chi tiết:

Lực hướng tâm tác dụng lên vật:

F_ht = ma_ht = mRω² = 2.5.2² = 40N

Đáp án - Lời giải

Câu hỏi 18 :

Một ô tô có khối lượng 1200kg chuyển động đều qua một đoạn cầu vượt dạng cung tròn với tốc độ là 36km/h. Biết bán kính cong của đoạn cầu vượt là 50m. Lấy g = 10m/s². Áp lực của ô tô lên mặt đường tại điểm cao nhất là

A 11950N
B 11760N
C 14400N
D 9600N

Đáp án: D

Phương pháp giải:

Tại điểm cao nhất hợp lực của N và P đóng vai trò lực hướng tâm.

N hướng lên trên, P hướng xuống dưới.

Công thức tính lực hướng tâm: \({{F}_{ht}}=m\frac{{{v}^{2}}}{R}\)

Lời giải chi tiết:

Tại điểm cao nhất hợp lực của N và P đóng vai trò lực hướng tâm.

N hướng lên trên, P hướng xuống dưới nên F_ht = P – N

Ta có: \(P-N={{F}_{ht}}=\frac{m{{v}^{2}}}{R}\Rightarrow N=P-\frac{m{{v}^{2}}}{R}=mg-\frac{m{{v}^{2}}}{R}\)

Với m = 1200kg ; v = 36km/h = 10m/s ; R = 50m

Thay vào ta được N = 9600N

Đáp án - Lời giải

Câu hỏi 19 :

Một quả cầu có khối lượng m = 50 (g) treo ở đầu B của sợi dây OB = l = 90cm. Quay cho quả cầu chuyển động tròn trong mặt phẳng thẳng đứng quanh tâm O. Tìm lực căng của dây khi B ở vị trí thấp hơn O, OB hợp với phương thẳng đứng một góc 60⁰ và vận tốc quả cầu khi đó là 3 (m/s), lấy g = 10m/s².

Phương pháp giải:

Vẽ hình và phân tích lực

Viết phương trình định luật II NiuTơn:

\(\vec T + \vec P = m.{\vec a_{ht}}\,\,\,(1)\)

Chiếu (1) lên trục hướng tâm

Công thức gia tốc hướng tâm:

\({a_{ht}} = m\frac{{{v^2}}}{l}\)

Lời giải chi tiết:

Tóm tắt:

m = 50 (g) treo ở đầu B của sợi dây OB = l = 90 cm.

Quả cầu chuyển động tròn trong mặt phẳng thẳng đứng quanh tâm O.

Tìm T khi B ở vị trí thấp hơn O, OB hợp với phương thẳng đứng một góc 60⁰ và v = 3 (m/s), g = 10m/s².

Giải :

Ta có hình vẽ:

- Phương trình định luật II NiuTơn:

\(\vec T + \vec P = m.{\vec a_{ht}}\,\,(1)\)

- Chiếu (1) lên trục hướng tâm:

\(T - P.cos{60^0} = \frac{{m{v^2}}}{l}\, \Rightarrow T = m.\left( {g.cos{{60}^0} + \frac{{{v^2}}}{l}} \right) = 0,75(N)\)

Đáp án - Lời giải

Câu hỏi 20 :

Một vật có khối lượng 0,1 kg chuyển động tròn đều trên đường tròn có bán kính r = 100 cm với tốc độ góc ω = 10 rad/s. Lực hướng tâm tác dụng lên vật có độ lớn bằng

A 14 N
B 10 N
C 16 N
D 12 N

Đáp án: B

Phương pháp giải:

Áp dụng công thức tính lực hướng tâm:

\({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r\)

Lời giải chi tiết:

Độ lớn lực hướng tâm: \({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.r\) = 0,1.10².1 = 10 N

Chọn B

Đáp án - Lời giải

Câu hỏi 21 :

Một xe đua chạy quanh một đường tròn nằm ngang, bán kính 500m. Vận tốc của xe không đổi có độ lớn 50m/s. Khối lượng xe là 1500kg. Độ lớn của lực hướng tâm của chiếc xe là :

A 15000N
B 7500N
C 12000N
D 5000N

Đáp án: B

Phương pháp giải:

Lực hướng tâm : \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{R} = m{\omega ^2}R\)

Lời giải chi tiết:

Có : \(\left\{ \begin{array}{l}v = 50m/s\\R = 500m\\m = 1500kg\end{array} \right. \Rightarrow {F_{ht}} = \dfrac{{m{v^2}}}{R} = \dfrac{{{{1500.50}^2}}}{{500}} = 7500N\)

Chọn B.

Đáp án - Lời giải

Câu hỏi 22 :

Một vệ tinh nhân tạo bay quanh Trái Đất ở độ cao h bằng bán kính R của Trái Đất. Cho R = 6 400km và lấy g = 10m/s². Hãy tính tốc độ và chu kì quay của vệ tinh.

A \(v = 3656,9m/s;T = 34217s\)
B \(v = 5656,9m/s;T = 14217s\)
C \(v = 4656,9m/s;T = 24217s\)
D \(v = 6656,9m/s;T = 44217s\)

Đáp án: B

Phương pháp giải:

+ Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\)

Trong đó G là hằng số hấp dẫn, có giá trị bằng: \(G = 6,{67.10^{ - 11}}\dfrac{{N.{m^2}}}{{k{g^2}}}\)

+ Lực hướng tâm : \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{R} = m{\omega ^2}R\)

+ Công thức tính tốc độ dài và chu kì

Lời giải chi tiết:

Khối lượng của Trái Đất và vệ tinh lần lượt là M và m.

Bán kính của Trái Đất là R = 6400km.

Vệ tinh nhân tạo bay quanh Trái Đất ở độ cao h = R

→ Khoảng cách từ vệ tinh đến tâm Trái Đất là: \(r = R + h = R + R = 2R\)

Khi vệ tinh chuyển động tròn đều quanh Trái Đất, lực hấp dẫn của Trái Đất tác dụng lên vệ tinh đóng vai trò là lực hướng tâm. Ta có:

\({F_{hd}} = {F_{ht}} \Leftrightarrow \dfrac{{GmM}}{{{{\left( {R + h} \right)}^2}}} = \dfrac{{m{v^2}}}{{\left( {R + h} \right)}} \Rightarrow v = \sqrt {\dfrac{{GM}}{{R + h}}} = \sqrt {\dfrac{{GM}}{{2R}}} \,\,\,\left( 2 \right)\)

Mặt khác: \(g = \dfrac{{GM}}{{{R^2}}} \Rightarrow GM = g{R^2}\,\,\,\left( 2 \right)\)

Thay (2) vào (1) ta có: \(v = \sqrt {\dfrac{{g{R^2}}}{{2R}}} = \sqrt {\dfrac{{gR}}{2}} \, = \sqrt {\dfrac{{{{10.6400.10}^3}}}{2}} = 5656,9m/s\)

Ta có: \(v = \omega r = \dfrac{{2\pi }}{T}.\left( {R + h} \right) \Rightarrow T = \dfrac{{2\pi .\left( {R + R} \right)}}{v} = \dfrac{{4\pi .R}}{v} = \dfrac{{4\pi {{.6400.10}^3}}}{{5656,9}} = 14217s\)

Chọn B.

Đáp án - Lời giải

Câu hỏi 23 :

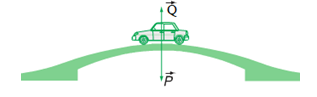
Một ô tô có khối lượng 1500kg chuyển động đều qua một đoạn cầu vượt (coi là cung tròn) với vận tốc 54km/h. Biết bán kính cong của đoạn cầu vượt là 25m. Lấy g = 10m/s². Áp lực của ô tô vào mặt đường tại điểm cao nhất bằng :

A 10950N
B 11560N
C 9600N
D 9000N

Đáp án: D

Phương pháp giải:

Xét chuyển động tròn đều của ô tô. Ta có : \(\overrightarrow Q + \overrightarrow P = \overrightarrow {{F_{ht}}} \,\,\,\left( * \right)\)

Lực hướng tâm : \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{R} = m{\omega ^2}R\)

Lời giải chi tiết:

Xét chuyển động tròn đều của ô tô. Ta có : \(\overrightarrow Q + \overrightarrow P = \overrightarrow {{F_{ht}}} \,\,\,\left( * \right)\)

Chiếu biểu thức (*) lên phương bán kính hướng vào tâm ta được :

\( - Q + P = {F_{ht}} \Rightarrow Q = P - {F_{ht}} = mg - \dfrac{{m{v^2}}}{R}\)

Mặt khác áp lực N luôn bằng phản lực Q

→ Áp lực của ô tô lên mặt cầu lúc này bằng :

\(N = Q = mg - \dfrac{{m{v^2}}}{R} = 1500.15 - 1500.\dfrac{{{{15}^2}}}{{25}} = 9000N\)

Chọn D.

Đáp án - Lời giải

Câu hỏi 24 :

Diễn viên xiếc (khối lượng tổng cộng là 60kg) đi xe đạp trên vòng xiếc bán kính 6,4m. Lấy g = 10m/s². Để đi qua điểm cao nhất mà không rơi thì người đó phải đi với tốc độ tối thiểu bằng :

A 15m/s
B 8m/s
C 12m/s
D 9,3m/s

Đáp án: B

Phương pháp giải:

Để không bị rơi xuống thì lực ép:\(N \ge 0\)

Lực hướng tâm : \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{R} = m{\omega ^2}R\)

Lời giải chi tiết:

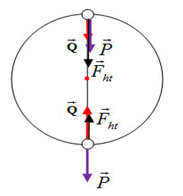
Để không bị rơi xuống thì \(N \ge 0\) (lực ép)

Xét chuyển động của diễn viên tại điểm cao nhất ta có: \(\overrightarrow P + \overrightarrow Q = \overrightarrow {{F_{ht}}} \,\,\,\left( * \right)\)

Chiếu (*) theo phương bán kính hướng vào tâm ta được:

\(P + Q = {F_{ht}} \Rightarrow Q = {F_{ht}} - P = \dfrac{{m{v^2}}}{R} - mg\)

Mà \(N = Q \Rightarrow N = \dfrac{{m{v^2}}}{R} - mg\)

Để người không rơi khỏi vòng xiếc tại vị trí cao nhất thì:

\(\begin{array}{l}N \ge 0 \Leftrightarrow \dfrac{{m{v^2}}}{R} - mg \ge 0 \Rightarrow v \ge \sqrt {gR} \Leftrightarrow v \ge \sqrt {10.6,4} \\v \ge 8m/s \Rightarrow {v_{\min }} = 8m/s\end{array}\)

Chọn B.

Đáp án - Lời giải

Câu hỏi 25 :

Biểu thức tính độ lớn của lực hướng tâm là :