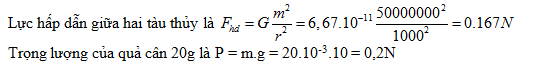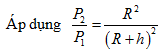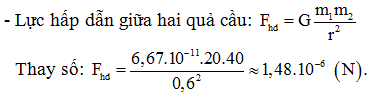Lời giải chi tiết:

Lời giải chi tiết:

Lời giải chi tiết:

Độ lớn lực tác dụng vào vật là

Trọng lực của vật là P = m.g = 8.10 = 80N

Ta thấy độ lớn lực gây ra gia tốc nhỏ hơn trọng lực của vật

Lời giải chi tiết:

Phương pháp giải:

Áp dụng công thức tính lực hấp dẫn. F = Gm₁m₂/r²

Lời giải chi tiết:

Lực hấp dẫn giữa Trái Đất và Mặt Trăng:

\(F=G\frac{m{}_{1}{{m}_{2}}}{{{r}^{2}}}={{6,67.10}^{-11}}.\frac{{{6.10}^{24}}{{.7,2.10}^{22}}}{{{({{38.10}^{7}})}^{2}}}={{2.10}^{20}}N\)

Phương pháp giải:

Áp dụng công thức tính lực hấp dẫn: \(F = G\frac{{mM}}{{{{\left( {R + h} \right)}^2}}}\)

Lời giải chi tiết:

Trọng lượng của phi hành gia tại mặt đất là:

\(P = G\frac{{mM}}{{{R^2}}} = 700\,\,\left( N \right)\)

Tại điểm cách tâm trái đất 5R thì trọng lượng của người đó là:

\(P' = G\frac{{mM}}{{R{'^2}}} = G\frac{{mM}}{{{{\left( {5R} \right)}^2}}} = \frac{1}{{25}}G\frac{{mM}}{{{R^2}}} = \frac{1}{{25}}P = \frac{1}{{25}}.700 = 28\,\,\left( N \right)\)

Phương pháp giải:

Công thức lực hấp dẫn 

\(F = G.\frac{{{m_1}.{m_2}}}{{{r^2}}}\)

, sau khi tính được lực hấp dẫn, ta có thẻ tính được gia tốc của các vật khi chịu tác dụng của lực này bằng định luật II Niu – Tơn: F = m.a để xét xem chúng có chuyển động lại gần nhau hay không?

Lời giải chi tiết:

a) Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai chất điểm bất kỳ tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

Công thức lực hấp dẫn \(F = G.\frac{{{m_1}.{m_2}}}{{{r^2}}}\). 

b)

Lực hấp dẫn giữa hai tàu là

\(F = G.{{{m_1}.{m_2}} \over {{r^2}}} \Leftrightarrow F = {6,67.10^{ - 11}}.{{100000000.100000000} \over {{{500}^2}}} = 2,668N\)

Lực hút này quá nhỏ, nên hai tàu không tiến hại gần nhau được

Ta có thể thử tính gia tốc của hai tàu khi chịu tác dụng của lực này

\(a = \frac{F}{m} = \frac{{2,668}}{{100000000}} = 2,{668.10^{ - 8}}m/{s^2}\)

Phương pháp giải:

Định luật vạn vật hấp dẫn : Lực hấp dẫn giữa hai chất điểm bất kỳ tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khảng cách giữa chúng.  

            \({F_{hd}} = G\frac{{{m_1}{m_2}}}{{{r^2}}}\)

Áp dụng thay số vào biểu thức trên

Lời giải chi tiết:

Định luật vạn vật hấp dẫn : Lực hấp dẫn giữa hai chất điểm bất kỳ tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khảng cách giữa chúng.              

            \({F_{hd}} = G\frac{{{m_1}{m_2}}}{{{r^2}}}\)

Áp dụng : m₁= m₂ = 45kg; r = 10cm = 0,1m

Lực hấp dẫn giữa chúng có độ lớn:    \({F_{hd}} = {6,67.10^{ - 11}}\frac{{45.45}}{{{{0,1}^2}}} = {1,35.10^{ - 5}}N\)

Phương pháp giải:

Áp dụng công thức tính lực hấp dẫn \({{F}_{hd}}=G\frac{Mm}{{{\left( R+h \right)}^{2}}}\)

Lời giải chi tiết:

Đáp án B

+ Lực hút của Trái Đất lên vật ở độ cao \(h\) được xác định bằng biểu thức \({{F}_{hd}}=G\frac{Mm}{{{\left( R+h \right)}^{2}}}\).

$\left\{ \matrix{
{F_h} = G{{Mm} \over {{{\left( {R + h} \right)}^2}}} = 5 \hfill \cr
{F_0} = G{{Mm} \over {{R^2}}} = 45 \hfill \cr} \right.N = > {{h + R} \over R} = 3 = > h = 2R$

Phương pháp giải:

Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\)

Trong đó G là hằng số hấp dẫn, có giá trị bằng: \(G = 6,{67.10^{ - 11}}\dfrac{{N.{m^2}}}{{k{g^2}}}\)

Lời giải chi tiết:

Ta có: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\)

Theo bài ra ta có : \(\left\{ \begin{array}{l}{m_1}' = 3{m_1}\\{m_2}' = 3{m_2}\\r' = 3r\end{array} \right. \Rightarrow {F_{hd}}' = \dfrac{{G.3{m_1}.3{m_2}}}{{{{\left( {3r} \right)}^2}}} = \dfrac{{G.{m_1}.{m_2}}}{{{r^2}}} = {F_{hd}}\)

Chọn D.

Phương pháp giải:

Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\)

Trong đó G là hằng số hấp dẫn, có giá trị bằng: \(G = 6,{67.10^{ - 11}}\dfrac{{N.{m^2}}}{{k{g^2}}}\)

Lời giải chi tiết:

Khoảng cách giữa tâm hai quả cầu là: \(r = 25dm = 2,5m\)

Lực hấp dẫn giữa hai quả cầu: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}} = \dfrac{{6,{{67.10}^{ - 11}}{{.2000}^2}}}{{2,{5^2}}} = 4,{2688.10^{ - 5}}N\)

Chọn A.

Phương pháp giải:

Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\)

Trong đó G là hằng số hấp dẫn, có giá trị bằng: \(G = 6,{67.10^{ - 11}}\dfrac{{N.{m^2}}}{{k{g^2}}}\)

Lời giải chi tiết:

Bán kính của mỗi quả cầu: \(R = 50cm = 0,5m\)

Ta có: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}} \Rightarrow {\left( {{F_{hd}}} \right)_{\max }} \Leftrightarrow {r_{\min }}\)

Lực hấp dẫn lớn nhất khi hai quả cầu tiếp xúc nhau \( \Rightarrow {r_{\min }} = {R_1} + {R_2} = 2R = 2.0,5 = 1m\)

\( \Rightarrow {F_{hd\max }} = \dfrac{{G{m_1}{m_2}}}{{r_{\min }^2}} = \dfrac{{6,{{67.10}^{ - 11}}{{.500}^2}}}{{{1^2}}} = 1,{6675.10^{ - 5}}N\)

Chọn C.

Phương pháp giải:

+ Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai chất điểm bất kì tỉ lệ thuận với tích hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng: \({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}\)

Trong đó G là hằng số hấp dẫn, có giá trị bằng: \(G = 6,{67.10^{ - 11}}\dfrac{{N.{m^2}}}{{k{g^2}}}\)

+ Công thức trọng lượng của vật: \(P = m.g\)

Lời giải chi tiết:

Lực hấp dẫn giữa hai tàu là:

\({F_{hd}} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}} = \dfrac{{6,{{67.10}^{ - 11}}.100\,{{000.10}^3}.100\,{{000.10}^3}}}{{{{500}^2}}} = 2,668N\)

Trọng lượng của một quả cân có khối lượng 50g là:

\(P = mg = {50.10^{ - 3}}.10 = 0,5N < {F_{hd}}\)

Chọn A.

Phương pháp giải:

Trọng lượng của vật: \(P = mg = G.\dfrac{{m.M}}{{{{\left( {R + h} \right)}^2}}}\)

Trong đó: h là độ cao của vật so với mặt đất.

Lời giải chi tiết:

Trọng lượng trên mặt đất (h = 0): \(P = mg = G.\dfrac{{m.M}}{{{R^2}}}\)

Trọng lượng ở độ cao h (h ≠ 0): \(P' = mg' = G.\dfrac{{m.M}}{{{{\left( {R + h} \right)}^2}}}\)

Để \(P' = \dfrac{1}{9}P \Leftrightarrow \dfrac{P}{{P'}} = 9 \Leftrightarrow \dfrac{g}{{g'}} = \dfrac{{{{\left( {R + h} \right)}^2}}}{{{R^2}}} = 9 \Leftrightarrow \dfrac{{R + h}}{R} = 3 \Rightarrow h = 2R = 12800km\)

Chọn D.

Phương pháp giải:

Trọng lượng của vật: \(P = mg = G.\dfrac{{m.M}}{{{{\left( {R + h} \right)}^2}}}\)

Trong đó: h là độ cao của vật so với mặt đất;  m là khối lượng của vật; M và R là khối lượng và bán kính của Trái Đất.

Lời giải chi tiết:

Độ lớn của trọng lực: \(P = mg = G.\dfrac{{m.M}}{{{{\left( {R + h} \right)}^2}}}\)

Tại mặt đất: \(h = 0 \Rightarrow {P_1} = mg = G.\dfrac{{m.M}}{{{R^2}}}\)

Ở độ cao cách tâm Trái Đất một khoảng 2R: \( \Rightarrow h = R \Rightarrow {P_2} = mg = G.\dfrac{{m.M}}{{{{\left( {R + R} \right)}^2}}} = G.\dfrac{{m.M}}{{4{R^2}}}\)

Lấy: \(\dfrac{{{P_2}}}{{{P_1}}} = \dfrac{{G.\dfrac{{m.M}}{{4{R^2}}}}}{{G.\dfrac{{m.M}}{{{R^2}}}}} = \dfrac{1}{4} \Rightarrow {P_2} = \dfrac{{{P_1}}}{4} = \dfrac{{20}}{4} = 5N\)

Chọn C.

Phương pháp giải:

Công thức tính gia tốc trọng trường tại mặt đất là và ở độ sâu d so với mặt đất:

\(\left\{ \begin{array}{l}{g_0} = \dfrac{{GM}}{{{R^2}}}\\{g_d} = \dfrac{{GM.\left( {R - d} \right)}}{{{R^3}}}\end{array} \right. \Rightarrow {g_d} = {g_0}.\dfrac{{R - d}}{R}\)

Lời giải chi tiết:

Ở độ sâu d so với mặt đất, gia tốc rơi tự do của một vật là: \({g_d} = g\dfrac{{\left( {R - d} \right)}}{R}\)

Chọn C.

Phương pháp giải:

Trọng lượng của một vật trên mặt đất : \(P = G.\dfrac{{mM}}{{{R^2}}}\)

Trọng lượng của một vật ở độ cao h : \({P_h} = G.\dfrac{{mM}}{{{{\left( {R + h} \right)}^2}}}\)

Lời giải chi tiết:

Vật ở trên mặt đất : \(P = G.\dfrac{{mM}}{{{R^2}}} = 9N\)

Khi chuyển vật tới một điểm cách tâm Trái Đất 3R :

\({P_h} = G.\dfrac{{mM}}{{{{\left( {3R} \right)}^2}}} = \dfrac{1}{9}G.\dfrac{{mM}}{{{R^2}}} = \dfrac{P}{9} = \dfrac{9}{9} = 1N\)

Chọn D.

Phương pháp giải:

Trọng lực của một vật là lực hấp dẫn giữa Trái Đất và vật đó

Lời giải chi tiết:

Một người khối lượng 50kg hút Trái Đất với một lực bằng :

\(P = m.g = 9,81.50 = 490,5N\)

Chọn A.

Phương pháp giải:

Áp dụng công thức gia tốc rơi tự do

Lời giải chi tiết:

Ta có g = GM/(R+h)²

Tại mặt đất có h = 0:                           GM/(R)²  = 9,8

Tại độ cao 1/5 bán kính trái đất: g’ = GM/(R+R/5)²= 6,8m/s²

Phương pháp giải:

Áp dụng công thức tính lực đàn hồi và biểu thức định luật 2 Niu tơn

Lời giải chi tiết:

a) Khi m = 200g = 0,2kg. Vật cân bằng:

                                    P = F_đh

                                mg = k(l – l₀)

                        k = 200N/m

b) Treo thêm vật Δm, vật cân bằng:

                                    P’ = F_đh’

                                    (m + Δm)g = k.0,06                

                                    Δm = 1kg