30 bài tập trắc nghiệm tích của một vecto với một số
Làm đề thiCâu hỏi 1 :
Với hai véc tơ không cùng phương \(\overrightarrow a \) và \(\overrightarrow b \). Xét hai véc tơ \(\overrightarrow u = 2\overrightarrow a - 3\overrightarrow b \)và \(\overrightarrow v = \overrightarrow a + \left( {x - 1} \right)\overrightarrow b \). Tìm \(x\) để \(\overrightarrow u \)và \(\overrightarrow v \) cùng phương.
- A \(x = \dfrac{1}{2}\).
- B \(x = - \dfrac{3}{2}\).
- C \(x = - \dfrac{1}{2}\).
- D \(x = \dfrac{3}{2}\).
Đáp án: C
Phương pháp giải:
Hai véctơ \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương khi và chỉ khi tồn tại hằng số \(k \ne 0\) sao cho \(\overrightarrow u = k\overrightarrow v \).
Lời giải chi tiết:
Để \(\overrightarrow u = 2\overrightarrow a - 3\overrightarrow b \)và \(\overrightarrow v = \overrightarrow a + \left( {x - 1} \right)\overrightarrow b \) cùng phương thì \(\dfrac{{x - 1}}{{ - 3}} = \dfrac{1}{2} \Leftrightarrow x - 1 = - \dfrac{3}{2} \Leftrightarrow x = - \dfrac{1}{2}.\)
Chọn: C.
Câu hỏi 2 :
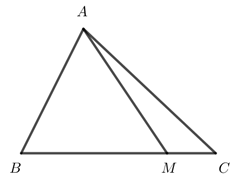
Cho tam giác ABC, lấy điểm M trên cạnh BC sao cho BM = 3MC. Biểu diễn \(\overrightarrow {AM} \) theo 2 vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) ta được:
- A \(\overrightarrow {AM} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)
- B
\(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
- C \(\overrightarrow {AM} = \frac{4}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
- D
\(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{4}{3}\overrightarrow {AC} \)
Đáp án: B
Phương pháp giải:
Sử dụng quy tắc 3 điểm để cộng vectơ.
Lời giải chi tiết:
\(\begin{array}{l}\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \\\overrightarrow {AM} = \overrightarrow {AB} + \frac{3}{4}\overrightarrow {BC} \\\overrightarrow {AM} = \overrightarrow {AB} + \frac{3}{4}\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\\\overrightarrow {AM} = \overrightarrow {AB} - \frac{3}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \\\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \end{array}\)
Đáp án B.
Câu hỏi 3 :
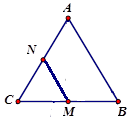
Cho tam giác \(ABC\) có \(M,\,\,N\) lần lượt là trung điểm của cạnh \(AB,\,\,AC.\) Gọi \(K\) là trung điểm \(MN.\) Hãy biểu diễn vectơ \(\overrightarrow {AK} \) theo hai vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} .\)
- A \(\overrightarrow {AK} = - \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} .\)
- B \(\overrightarrow {AK} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\)
- C \(\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} .\)
- D \(\overrightarrow {AK} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} .\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức trung điểm.
Lời giải chi tiết:
\(\overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AM} + \overrightarrow {AN} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} .\)
Chọn C.
Câu hỏi 4 :
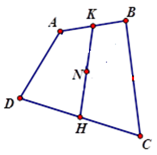
Cho tứ giác \(ABCD\). Xác định điểm \(N\) sao cho \(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} + \overrightarrow {ND} = \overrightarrow 0 \)
- A N là trung điểm của KH, K, H lần lượt là trung điểm của AC, BD.
- B N là trung điểm của KH, K, H lần lượt là trọng tâm tam giác ABC, BCD.
- C N là trung điểm của KH, K, H lần lượt là trung điểm của AD, BC.
- D N là trung điểm của KH, K, H lần lượt là trung điểm của AB, CD.
Đáp án: D
Phương pháp giải:
Áp dụng quy tắc trung điểm.
Lời giải chi tiết:
Gọi K, H lần lượt là trung điểm của AB, CD ta có
\(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} + \overrightarrow {ND} = \overrightarrow 0 \Leftrightarrow 2\overrightarrow {NK} + 2\overrightarrow {NH} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {NK} + \overrightarrow {NH} = \overrightarrow 0 \Leftrightarrow N\) là trung điểm của \(KH.\)
Chọn D.
Câu hỏi 5 :
Cho tứ giác \(ABCD\). Xác định điểm \(M,\,N,\,P\) sao cho \(3\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} = \overrightarrow 0 \)
- A P là trung điểm \(AG,\,\,G\) là trọng tâm tam giác \(ACD.\)
- B P là trung điểm \(AG,\,\,G\) là trọng tâm tam giác \(BAD.\)
- C P là trung điểm \(AG,\,\,G\) là trọng tâm tam giác \(BCD.\)
- D P là trung điểm \(AG,\,\,G\) là trọng tâm tam giác \(ABC.\)
Đáp án: C
Phương pháp giải:
Áp dụng quy tắc trung điểm và trọng tâm tam giác.
Lời giải chi tiết:
Gọi \(G\) là trọng tâm tam giác \(BCD\) khi đó ta có \(\overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} = 3\overrightarrow {PG} \)
Suy ra: \(3\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} = \overrightarrow 0 \Leftrightarrow 3\overrightarrow {PA} + 3\overrightarrow {PG} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {PA} + \overrightarrow {PG} = \overrightarrow 0 \Leftrightarrow P\) là trung điểm \(AG\).
Chọn C.
Câu hỏi 6 :
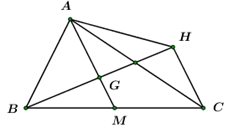
Cho tam giác ABC. Gọi H là điểm đối xứng với B qua G với G là trọng tâm tam giác. Chọn khẳng định đúng?
- A \(\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \)
- B \(\overrightarrow {CH} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
- C Cả A, B đều đúng
- D Cả A, B đều sai
Đáp án: C
Phương pháp giải:
Áp dụng quy tắc hình bình hành, quy tắc trung điểm để tách và rút gọn.
Lời giải chi tiết:
Áp dụng quy tắc hình bình hành ta có:
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {AH} = 2\overrightarrow {AG} \\ \Rightarrow \overrightarrow {AH} = 2\overrightarrow {AG} - \overrightarrow {AB} = \frac{2}{3}\overrightarrow {AM} - \overrightarrow {AB} \\ = \frac{2}{3}\left( {\overrightarrow {AC} + \overrightarrow {AB} } \right) - \overrightarrow {AB} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \\ \Rightarrow \overrightarrow {CH} = \overrightarrow {AH} - \overrightarrow {AC} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} .\end{array}\)
Chọn C.
Câu hỏi 7 :
Cho tứ giác \(ABCD\). Gọi I, J lần lượt là trung điểm của AB và CD. Khẳng định nào sau đây đúng?
- A \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {IJ} \)
- B \(\overrightarrow {AC} + \overrightarrow {BD} = \frac{1}{2}\overrightarrow {IJ} \)
- C \(\overrightarrow {AC} + \overrightarrow {BD} = 3\overrightarrow {IJ} \)
- D \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {IJ} \)
Đáp án: D
Phương pháp giải:
Áp dụng quy tắc 3 điểm, quy tắc trung điểm để tách và triệt tiêu.
Lời giải chi tiết:
Theo quy tắc ba điểm ta có: \(\overrightarrow {AC} = \overrightarrow {AI} + \overrightarrow {IJ} = \overrightarrow {AI} + \overrightarrow {IJ} + \overrightarrow {JC} \)
Tương tự: \(\overrightarrow {BD} = \overrightarrow {BI} + \overrightarrow {IJ} + \overrightarrow {JD} \)
Mà I, J lần lượt là trung điểm của AB và CD nên \(\overrightarrow {AI} + \overrightarrow {BI} = \overrightarrow 0 ,\,\,\overrightarrow {JC} + \overrightarrow {JD} = \overrightarrow 0 \)
Vậy \(\overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AI} + \overrightarrow {BI} } \right) + \left( {\,\,\overrightarrow {JC} + \overrightarrow {JD} } \right) + 2\overrightarrow {IJ} = 2\overrightarrow {IJ} .\)
Chọn D.
Câu hỏi 8 :
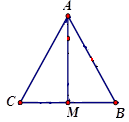
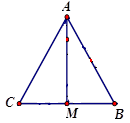
Cho tam giác đều \(ABC\) cạnh a, điểm \(M\) là trung điểm \(BC\). Tính độ dài của \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \)
- A \(a\)
- B \(2a\)
- C \(3a\)
- D \(4a\)
Đáp án: A
Phương pháp giải:
Biến đổi để áp dụng quy tắc 3 điểm.
Lời giải chi tiết:
Do \(\frac{1}{2}\overrightarrow {CB} = \overrightarrow {CM} \) suy ra theo quy tắc ba điểm ta có:
\(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} = \overrightarrow {CM} + \overrightarrow {MA} = \overrightarrow {CA} \)
Vậy \(\left| {\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} } \right| = CA = a.\)
Chọn A.
Câu hỏi 9 :
Cho \(\Delta ABC,\) gọi \(M\) là điểm thuộc cạnh \(BC\) sao cho \(BM = 3MC.\) Khẳng định nào sau đây là khẳng định đúng?
- A \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
- B \(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
- C \(\overrightarrow {AM} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)
- D \(\overrightarrow {AM} = \frac{5}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
Đáp án: B
Phương pháp giải:
Áp dụng quy tắc cộng vecto.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{3}{4}\overrightarrow {BC} = \overrightarrow {AB} + \frac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} .\)
Chọn B.
Câu hỏi 10 :
Cho tam giác đều \(ABC\) cạnh a. Tính độ dài của \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \)
- A \(\frac{{a\sqrt 3 }}{4}\)
- B \(\frac{{a\sqrt 3 }}{2}\)
- C \(\frac{{a\sqrt 3 }}{5}\)
- D \(\frac{{a\sqrt 3 }}{6}\)
Đáp án: B
Phương pháp giải:
Gọi M là trung điểm của BC. Áp dụng quy tắc trừ và định lý Pitago để tính
Lời giải chi tiết:
Gọi M là trung điểm của BC.
Vì \(\frac{1}{2}\overrightarrow {BC} = \overrightarrow {BM} \) nên theo quy tắc trừ ta có \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} = \overrightarrow {BA} - \overrightarrow {BM} = \overrightarrow {MA} \)
Theo định lí Pitago ta có: \(MA = \sqrt {A{B^2} - B{M^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Vậy \(\left| {\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} } \right| = MA = \frac{{a\sqrt 3 }}{2}\)
Chọn B.
Câu hỏi 11 :
Cho tam giác \(ABC\). Xác định điểm \(M\) sao cho \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
- A M là trung điểm AE, với E là trung điểm AC
- B M là trung điểm AF, với F là trung điểm AB
- C M là trung điểm AG, với G là trọng tâm ABC
- D M là trung điểm AI, với I là trung điểm BC
Đáp án: D
Phương pháp giải:
Áp dụng quy tắc trung điểm.
Lời giải chi tiết:
Gọi I là trung điểm BC suy ra \(\overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MI} \)
Do đó \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {MA} + 2\overrightarrow {MI} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MI} = \overrightarrow 0 \)
Suy ra M là trung điểm AI.
Chọn D.
Câu hỏi 12 :
Cho tam giác đều \(ABC\) cạnh a. Gọi điểm \(M\), \(N\) lần lượt là trung điểm \(BC,\,\,CA\). Tính độ dài của \(\frac{1}{2}\overrightarrow {BC} - 2\overrightarrow {MN} \)
- A \(\frac{{7a\sqrt 3 }}{2}\)
- B \(\frac{{a\sqrt 3 }}{2}\)
- C \(\frac{{5a\sqrt 3 }}{2}\)
- D \(\frac{{3a\sqrt 3 }}{2}\)
Đáp án: B
Phương pháp giải:
Sử dụng tính chất trung điểm .
Đường trung tuyến của tam giác đều cạnh \(a\) có độ dài bằng \(\frac{{a\sqrt 3 }}{2}.\)
Lời giải chi tiết:
Theo quy tắc trừ ta có: \(\frac{1}{2}\overrightarrow {BC} - 2\overrightarrow {MN} = \overrightarrow {BM} - \overrightarrow {BA} = \overrightarrow {AM} \)
\( \Rightarrow \left| {\frac{1}{2}\overrightarrow {BC} - 2\overrightarrow {MN} } \right| = AM = \frac{{a\sqrt 3 }}{2}\)
Chọn B.
Câu hỏi 13 :
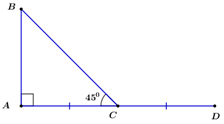
Cho tam giác ABC vuông có \(AB = AC = 3\). Tích vô hướng \(\overrightarrow {AC} .\overrightarrow {CB} \) bằng:
- A \(0\)
- B \(-9\)
- C \(3\)
- D \(9\)
Đáp án: B
Phương pháp giải:
Sử dụng tính chất tam giác vuông cân, định lý Pytago.
Công thức tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\)
Lời giải chi tiết:
Ta có tam giác ABC vuông có \(AB = AC = 3\)
\( \Rightarrow \)Tam giác ABC vuông cân tại A.
\( \Rightarrow \angle ACB = \angle ABC = {45^o}\) (định lý tổng 3 góc trong tam giác)
Gọi D là điểm đối xứng với A qua C \( \Rightarrow \angle BCD = {180^o} - \angle ACB = {135^o};\;CD = AC = 3;\;\overrightarrow {AC} = \overrightarrow {CD} .\)
Áp dụng định lý Pytago cho tam giác ABC vuông cân tại A\( \Rightarrow CB = \sqrt {A{B^2} + A{C^2}} = 3\sqrt 2 \)
\(\overrightarrow {AC} .\overrightarrow {CB} = \overrightarrow {CD} .\overrightarrow {CB} = \left| {\overrightarrow {CD} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {CD} ,\overrightarrow {CB} } \right) = CD.CB.\cos \angle BCD = 3.3\sqrt 2 .\cos {135^o} = - 9\)
Chọn B.
Câu hỏi 14 :
Vectơ \( - 2\overrightarrow a \) và vec tơ \(\overrightarrow a \;\;\;\left( {\overrightarrow a \ne \overrightarrow 0 } \right)\) là hai vectơ
- A Đối nhau
- B Ngược hướng
- C Bằng nhau
- D Cùng hướng
Đáp án: B
Phương pháp giải:
Cho 2 vectơ \(\overrightarrow a \;\;\left( {\overrightarrow a \ne 0} \right)\) và \(\overrightarrow b = k\overrightarrow a \)
+) Nếu \(k > 0\) thì 2 vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) cùng hướng.
+) Nếu \(k < 0\) thì 2 vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) ngược hướng.
Lời giải chi tiết:
Vectơ \( - 2\overrightarrow a \) và vectơ \(\overrightarrow a \;\;\left( {\overrightarrow a \ne 0} \right)\) là hai vectơ ngược hướng.
Chọn B.
Câu hỏi 15 :
Cho hình bình hành ABCD tâm O. I, J thỏa mãn: \(3\overrightarrow {IA} + 2\overrightarrow {IC} - 2\overrightarrow {ID} = \overrightarrow O ;\,\,\overrightarrow {JA} - 2\overrightarrow {JB} + 2\overrightarrow {JC} = \overrightarrow 0 \) . Chứng minh 3 điểm O, I, J thẳng hàng.
Lời giải chi tiết:
+) Chọn \(\overrightarrow {OA} ,\,\,\overrightarrow {OB} \) . Ta có:
\(\begin{array}{l}3\overrightarrow {IA} + 2\overrightarrow {IC} - 2\overrightarrow {ID} = 3\left( {\overrightarrow {OA} - \overrightarrow {OI} } \right) + 2\left( {\overrightarrow {OC} - \overrightarrow {OI} } \right) - 2\left( {\overrightarrow {OD} - \overrightarrow {OI} } \right)\\ = - 3\overrightarrow {OI} + 3\overrightarrow {OA} + 2\overrightarrow {OC} - 2\overrightarrow {OD} \\ = - 3\overrightarrow {OI} + 3\overrightarrow {OA} - 2\overrightarrow {OA} + 2\overrightarrow {OB} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {OI} = \frac{1}{3}\left( {\overrightarrow {OA} + 2\overrightarrow {OB} } \right)\,\,\,\left( 1 \right)\end{array}\)
+) Lại có:
\(\begin{array}{l}\overrightarrow {JA} - 2\overrightarrow {JB} + 2\overrightarrow {JC} = \left( {\overrightarrow {OA} - \overrightarrow {OJ} } \right) - 2\left( {\overrightarrow {OB} - \overrightarrow {OJ} } \right) + 2\left( {\overrightarrow {OC} - \overrightarrow {OJ} } \right)\\ = - \overrightarrow {OJ} + \overrightarrow {OA} - 2\overrightarrow {OB} + 2\overrightarrow {OC} \\ = - \overrightarrow {OJ} + \overrightarrow {OA} - 2\overrightarrow {OB} - 2\overrightarrow {OA} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {OJ} = - \overrightarrow {OA} - 2\overrightarrow {OB} \,\,\,\left( 2 \right)\end{array}\)
+) Từ (1) và (2) ta có: \(\overrightarrow {OI} = \frac{{ - 1}}{3}\overrightarrow {OJ} \) Suy ra 3 điểm O, I, J thẳng hàng.
Câu hỏi 16 :
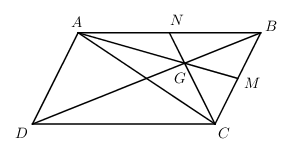
Cho hình bình hành ABCD có N là trung điểm của AB và G là trọng tâm tam giác ABC. Phân tích \(\overrightarrow {GA} \) theo \(\overrightarrow {BD} \) và \(\overrightarrow {NC} \)?
- A \(\overrightarrow {GA} = \frac{{ - 1}}{3}\overrightarrow {BD} + \frac{2}{3}\overrightarrow {NC} \)
- B \(\overrightarrow {GA} = \frac{1}{3}\overrightarrow {BD} - \frac{4}{3}\overrightarrow {NC} \)
- C \(\overrightarrow {GA} = \frac{1}{3}\overrightarrow {BD} + \frac{2}{3}\overrightarrow {NC} \)
- D \(\overrightarrow {GA} = \frac{1}{3}\overrightarrow {BD} - \frac{2}{3}\overrightarrow {NC} \)
Đáp án: D
Phương pháp giải:
Sử dụng công thức ba điểm, công thức trung điểm.
Lời giải chi tiết:
Gọi M là trung điểm của BC ta có: \(\overrightarrow {GA} = \frac{2}{3}\overrightarrow {MA} = \frac{{ - 2}}{3}\overrightarrow {AM} \)
\(\begin{array}{l}\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {AC} } \right)\\ = \frac{1}{2}\left( {\overrightarrow {BC} + \overrightarrow {DB} + \overrightarrow {AC} } \right) = \frac{{ - 1}}{2}\overrightarrow {BD} - \frac{1}{2}\left( {\overrightarrow {CB} + \overrightarrow {CA} } \right)\\ = \frac{{ - 1}}{2}\overrightarrow {BD} - \overrightarrow {CN} = \frac{{ - 1}}{2}\overrightarrow {BD} + \overrightarrow {NC} \\ \Rightarrow \overrightarrow {GA} = \frac{{ - 2}}{3}\left( {\frac{{ - 1}}{2}\overrightarrow {BD} + \overrightarrow {NC} } \right) = \frac{1}{3}\overrightarrow {BD} - \frac{2}{3}\overrightarrow {NC} \end{array}\)
Chọn đáp án D.
Câu hỏi 17 :
Cho tam giác ABC và điểm I thỏa mãn \(\overrightarrow {IA} = 3\overrightarrow {IB} \). Phân tích \(\overrightarrow {CI} \) theo \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \).
- A \(\overrightarrow {CI} = \frac{1}{2}\left( {\overrightarrow {CA} - 3\overrightarrow {CB} } \right)\)
- B \(\overrightarrow {CI} = \overrightarrow {CA} - 3\overrightarrow {CB} \)
- C \(\overrightarrow {CI} = \frac{1}{2}\left( {3\overrightarrow {CB} - \overrightarrow {CA} } \right)\)
- D \(\overrightarrow {CI} = 3\overrightarrow {CB} - \overrightarrow {CA} \)
Đáp án: C
Phương pháp giải:
Sử dụng công thức ba điểm.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\overrightarrow {CB} = \overrightarrow {CA} + \overrightarrow {AB} \,\,\,\,\,\,\left( 1 \right)\\\overrightarrow {CB} = \overrightarrow {CI} + \overrightarrow {IB} \Rightarrow 2\overrightarrow {CB} = 2\overrightarrow {CI} + 2\overrightarrow {IB} \,\,\,\left( 2 \right)\end{array}\)
Cộng vế theo vế của (1) với (2) ta được: \(3\overrightarrow {CB} = \overrightarrow {CA} + \overrightarrow {AB} + 2\overrightarrow {CI} + 2\overrightarrow {IB} \)
Do \(\overrightarrow {AB} = - 2\overrightarrow {IB} \Rightarrow \overrightarrow {AB} + 2\overrightarrow {IB} = \overrightarrow 0 \)
\( \Rightarrow 3\overrightarrow {CB} = \overrightarrow {CA} + 2\overrightarrow {CI} \Rightarrow 2\overrightarrow {CI} = 3\overrightarrow {CB} - \overrightarrow {CA} \Rightarrow \overrightarrow {CI} = \frac{1}{2}\left( {3\overrightarrow {CB} - \overrightarrow {CA} } \right)\).
Chọn đáp án C.
Câu hỏi 18 :
Cho tam giác OAB. Gọi M, N lần lượt là trung điểm của OA, OB . Khi đó, nếu \(\overrightarrow {MN} = m\overrightarrow {OA} + n\overrightarrow {OB} \) thì
- A
\(m + n = - 1\)
- B
\(m + n = 4\)
- C
\(m + n = 0\)
- D \(m + n = 1\)
Đáp án: C
Phương pháp giải:
+) Chứng minh MN là đường trung bình của tam giác ABC.
+) Sử dụng công thức ba điểm.
Lời giải chi tiết:
M, N lần lượt là trung điểm của OA, OB \( \Rightarrow \) MN là đường trung bình của tam giác OAB
\( \Rightarrow \overrightarrow {MN} = \frac{1}{2}\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {AO} + \overrightarrow {OB} } \right) = - \frac{1}{2}\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \)
Mà \(\overrightarrow {MN} = m\overrightarrow {OA} + n\overrightarrow {OB} \)
\(\begin{array}{l} \Rightarrow m = - \frac{1}{2},\,\,n = \frac{1}{2}\\ \Rightarrow m + n = 0\end{array}\)
Chọn: C
Câu hỏi 19 :
Cho \(\Delta {\rm{ABC}}\), M là điểm trên cạnh BC sao cho \(MB = 2MC\). Đẳng thức vectơ nào sau đây đúng?
- A
\(\overrightarrow {AM} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)
- B
\(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
- C
\(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
- D \(\overrightarrow {AM} = - \frac{3}{4}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
Đáp án: C
Phương pháp giải:
+) Từ tỉ số đoạn thẳng suy ra tỉ số vectơ.
+) Sử dụng công thức 3 điểm.
Lời giải chi tiết:
M là điểm trên cạnh BC sao cho MB = 2MC
\(\begin{array}{l} \Rightarrow \overrightarrow {MB} = - 2\overrightarrow {MC} \Leftrightarrow \overrightarrow {MA} + \overrightarrow {AB} = - 2\overrightarrow {MA} - 2\overrightarrow {AC} \Leftrightarrow 3\overrightarrow {MA} = - 2\overrightarrow {AC} - \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {AM} = \frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} \Leftrightarrow \overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \end{array}\)
Chọn: C
Câu hỏi 20 :
Cho tam giác \(ABC,{\rm{ }}M\) và \(N\) là hai điểm thỏa mãn: \(\overrightarrow {BM} = \overrightarrow {BC} - 2\overrightarrow {AB} ;\,\,\,\overrightarrow {CN} = x\overrightarrow {AC} - \overrightarrow {BC} .\) Xác định \(x\) để \(A,{\rm{ }}M,{\rm{ }}N\) thẳng hàng.
- A \(3.\)
- B \( - \dfrac{1}{3}.\)
- C \(2.\)
- D \( - \dfrac{1}{2}.\)
Đáp án: D
Phương pháp giải:
Để A, M, N thẳng hàng \( \Rightarrow \overrightarrow {AN} = k\overrightarrow {AM} \,\,\left( {k \in R} \right)\).
Lời giải chi tiết:
\(\begin{array}{l}
\,\,\,\,\,\overrightarrow {BM} = \overrightarrow {BC} - 2\overrightarrow {AB} \\
\Rightarrow - \overrightarrow {AB} + \overrightarrow {AM} = \overrightarrow {BC} - 2\overrightarrow {AB} \\
\Rightarrow \overrightarrow {AM} = \overrightarrow {BC} - \overrightarrow {AB} = \overrightarrow {BC} - \overrightarrow {AC} - \overrightarrow {CB} = 2\overrightarrow {BC} - \overrightarrow {AC} \\
\,\,\,\,\,\,\overrightarrow {CN} = x\overrightarrow {AC} - \overrightarrow {BC} \\
\Rightarrow - \overrightarrow {AC} + \overrightarrow {AN} = x\overrightarrow {AC} - \overrightarrow {BC} \\
\Leftrightarrow \overrightarrow {AN} = \left( {x + 1} \right)\overrightarrow {AC} - \overrightarrow {BC} \\
\Leftrightarrow \overrightarrow {AN} = - \overrightarrow {BC} + \left( {x + 1} \right)\overrightarrow {AC}
\end{array}\)
Để A, M, N thẳng hàng \( \Rightarrow \overrightarrow {AN} = k\overrightarrow {AM} \)
\( \Rightarrow \left\{ \begin{array}{l}
- 1 = 2k\\
x + 1 = - k
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
k = - \dfrac{1}{2}\\
x = - \dfrac{1}{2}
\end{array} \right.\)
Chọn D.
Câu hỏi 21 :
Cho tam giác \(ABC\) có \(I,{\rm{ }}D\) lần lượt là trung điểm\(AB,{\rm{ }}CI\). Đẳng thức nào sau đây đúng?
- A \(\overrightarrow {BD} = \dfrac{1}{2}\overrightarrow {AB} - \dfrac{3}{4}\overrightarrow {AC} \).
- B \(\overrightarrow {BD} = - \dfrac{3}{4}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AC} \).
- C \(\overrightarrow {BD} = - \dfrac{1}{4}\overrightarrow {AB} + \dfrac{3}{2}\overrightarrow {AC} \).
- D \(\overrightarrow {BD} = - \dfrac{3}{4}\overrightarrow {AB} - \dfrac{1}{2}\overrightarrow {AC} \).
Đáp án: B
Phương pháp giải:
Sử dụng công thức ba điểm và công thức trung điểm.
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\overrightarrow {BD} = \dfrac{1}{2}\left( {\overrightarrow {BI} + \overrightarrow {BC} } \right) = \dfrac{1}{2}.\dfrac{1}{2}\overrightarrow {BA} + \dfrac{1}{2}\overrightarrow {BC} = \dfrac{1}{4}\overrightarrow {BA} + \dfrac{1}{2}\overrightarrow {BC} \\ = - \dfrac{1}{4}\overrightarrow {AB} + \dfrac{1}{2}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = - \dfrac{1}{4}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AC} - \dfrac{1}{2}\overrightarrow {AB} = - \dfrac{3}{4}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AC} \end{array}\)
Chọn B.
Câu hỏi 22 :
Cho tam giác ABC. Gọi M là trung điểm của AB, D là trung điểm của BC, N là điểm thuộc AC sao cho \(\overrightarrow {CN} = 2\overrightarrow {NA} \), K là trung điểm của MN. Khẳng định nào sau đây đúng?
- A \(\overrightarrow {KD} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
- B \(\overrightarrow {KD} = \frac{1}{4}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
- C \(\overrightarrow {KD} = 3\overrightarrow {AB} - 4\overrightarrow {AC} \)
- D \(\overrightarrow {KD} = 4\overrightarrow {AB} + 3\overrightarrow {AC} \)
Đáp án: A
Phương pháp giải:
Sử dụng hệ thức trung điểm đoạn thẳng và quy tắc 3 điểm để tìm mối qua hệ giữa \(\overrightarrow {KD} ,\,\,\overrightarrow {AB} ,\,\,\overrightarrow {AC} \)
Quy tắc trung điểm: M là trung điểm của AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \) và với I bất kì ta có: \(\overrightarrow {IA} + \overrightarrow {IB} = 2\overrightarrow {IM} .\)
Lời giải chi tiết:
Ta có M là trung điểm của AB \( \Rightarrow \overrightarrow {MB} = \frac{1}{2}\overrightarrow {AB} \)
N là điểm thuộc AC sao cho \(\overrightarrow {CN} = 2\overrightarrow {NA} \Rightarrow \overrightarrow {NC} = \frac{2}{3}\overrightarrow {AC} \)
K là trung điểm của MN \( \Rightarrow \overrightarrow {KM} + \overrightarrow {KN} = \overrightarrow 0 \)
Ta có D là trung điểm của BC \( \Rightarrow \overrightarrow {KB} + \overrightarrow {KC} = 2\overrightarrow {KD} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {KD} = \frac{{\overrightarrow {KB} + \overrightarrow {KC} }}{2} = \frac{{\overrightarrow {KM} + \overrightarrow {MB} + \overrightarrow {KN} + \overrightarrow {NC} }}{2}\\ = \frac{{\left( {\overrightarrow {KM} + \overrightarrow {KN} } \right) + \frac{1}{2}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} }}{2} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\end{array}\)
Chọn A.
Câu hỏi 23 :
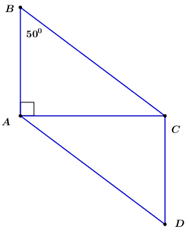
Cho tam giác ABC vuông tại A và có \(\angle B = {50^o}\). Hệ thức nào sau đây sai?
- A \(\left( {\overrightarrow {AB} ,\overrightarrow {CB} } \right) = {130^o}\)
- B \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {140^o}\)
- C \(\left( {\overrightarrow {BC} ,\overrightarrow {AC} } \right) = {40^o}\)
- D \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {50^o}\)
Đáp án: C
Phương pháp giải:
Sử dụng định lý tổng 3 góc trong tam giác, tứ giác, đưa các vectơ về cùng một gốc để tìm góc giữa chúng.
Lời giải chi tiết:
Lấy điểm D sao cho ABCD là hình bình hành
\( \Rightarrow \left\{ \begin{array}{l}\angle BAD = \angle BCD\\\angle ABC = \angle CDA\end{array} \right.\) (tính chất hình bình hành)
\( \Rightarrow \angle BAD = \dfrac{{{{360}^o} - 2.\angle B}}{2} = {130^o}\) (định lý tổng 4 góc trong tứ giác)
Ta có \(\overrightarrow {BC} = \overrightarrow {AD} \) (ABCD là hình bình hành)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \angle BAD = {130^o}\)
Chọn D.
Câu hỏi 24 :
Cho tam giác ABC với trọng tâm G . Đặt \(\overrightarrow {CA} = \overrightarrow a \,\,,\,\,\overrightarrow {CB} = \overrightarrow b \) . Biểu thị vectơ \(\overrightarrow {AG} \) theo hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ta được:
- A \(\overrightarrow {AG} = \frac{{2\overrightarrow a - \overrightarrow b }}{3}\)
- B \(\overrightarrow {AG} = \frac{{ - 2\overrightarrow a + \overrightarrow b }}{3}\)
- C \(\overrightarrow {AG} = \frac{{2\overrightarrow a + \overrightarrow b }}{3}\)
- D \(\overrightarrow {AG} = \frac{{\overrightarrow a - \overrightarrow {2b} }}{3}\)
Đáp án: B
Phương pháp giải:
Sử dụng các quy tắc cộng trừ vectơ để biến đổi \(\overrightarrow {AG} \) theo hai vectơ \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \)
G là trọng tâm của tam giác ABC \( \Rightarrow \overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 .\)
Lời giải chi tiết:
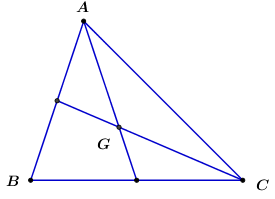
G là trọng tâm của tam giác ABC \( \Rightarrow \overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AG} = - \overrightarrow {BG} - \overrightarrow {CG} = - \overrightarrow {BC} - \overrightarrow {CA} - \overrightarrow {AG} - \overrightarrow {CA} - \overrightarrow {AG} \\ \Leftrightarrow \overrightarrow {AG} = \overrightarrow {CB} - 2\overrightarrow {CA} - 2\overrightarrow {AG} \\ \Leftrightarrow 3\overrightarrow {AG} = - 2\overrightarrow {CA} + \overrightarrow {CB} \\ \Rightarrow \overrightarrow {AG} = \frac{{ - 2\overrightarrow {CA} + \overrightarrow {CB} }}{3} = \frac{{ - 2\overrightarrow a + \overrightarrow b }}{3}.\end{array}\)
Chọn B.
Câu hỏi 25 :
Gọi điểm M là điểm thuộc cạnh BC của tam giác ABC sao cho BM = 3MC . Khi đó \(\overrightarrow {AM} \) bằng:
- A \(\frac{1}{2}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} \)
- B \(\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
- C \(\frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} \)
- D \(\frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)
Đáp án: B
Phương pháp giải:
Sử dụng quy tắc 3 điểm, các tính chất vectơ để tính \(\overrightarrow {AM} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{3}{4}\overrightarrow {BC} = \overrightarrow {AB} + \frac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)
\( = \overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
Chọn B.
Câu hỏi 26 :
Cho tam giác đều \(ABC\) cạnh a. Tính độ dài của \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} .\)
- A \(\frac{{a\sqrt {21} }}{3}\)
- B \(\frac{{a\sqrt {21} }}{2}\)
- C \(\frac{{a\sqrt {21} }}{4}\)
- D \(\frac{{a\sqrt {21} }}{7}\)
Đáp án: B
Phương pháp giải:
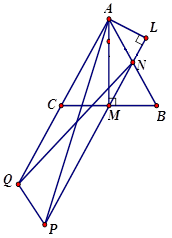
Gọi \(N\) là trung điểm \(AB\), \(Q\) là điểm đối xứng của \(A\) qua \(C\) và \(P\) là đỉnh của hình bình hành \(AQPN\)để áp dụng quy tắc hình bình hành. Gọi \(L\) là hình chiếu của \(A\) lên \(QN\) để tính.
Lời giải chi tiết:
Gọi \(N\) là trung điểm \(AB\), \(Q\) là điểm đối xứng của \(A\) qua \(C\) và \(P\) là đỉnh của hình bình hành \(AQPN\).
Khi đó ta có: \(\frac{1}{2}\overrightarrow {AB} = \overrightarrow {AN} ,\,\,2\overrightarrow {AC} = \overrightarrow {AQ} \)
Suy ra theo quy tắc hình bình hành ta có: \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow {AN} + \overrightarrow {AQ} = \overrightarrow {AP} \)
Gọi \(L\) là hình chiếu của \(A\) lên \(PN.\)
Vì \(MN//AC \Rightarrow \angle ANL = \angle MNB = \angle CAB = {60^0}\)
Xét tam giác vuông \(ANL\) ta có \(\begin{array}{l}\sin \angle ANL = \frac{{AL}}{{AN}} \Rightarrow AL = AN.\sin \angle ANL = \frac{a}{2}\sin {60^0} = \frac{{a\sqrt 3 }}{4}\\\cos \angle ANL = \frac{{NL}}{{AN}} \Rightarrow NL = AN.\cos \angle ANL = \frac{a}{2}\cos {60^0} = \frac{a}{4}\end{array}\)
Ta lại có: \(AQ = PN \Rightarrow PL = PN + NL = AQ + NL = 2a + \frac{a}{4} = \frac{{9a}}{4}\)
Áp dụng định lí Pitago trong tam giác \(ALP\) ta có:
\(A{P^2} = A{L^2} + P{L^2} = \frac{{3{a^2}}}{{16}} + \frac{{81{a^2}}}{{16}} = \frac{{21{a^2}}}{4} \Rightarrow AP = \frac{{a\sqrt {21} }}{2}\)
Vậy \(\left| {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} } \right| = AP = \frac{{a\sqrt {21} }}{2}.\)
Chọn B.
Câu hỏi 27 :
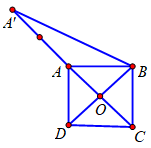
Cho hình vuông \(ABCD\) cạnh a. Tính độ dài vectơ \(\overrightarrow u = 4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \).
- A \(\left| {\overrightarrow u } \right| = a\sqrt 5 \)
- B \(\left| {\overrightarrow u } \right| = \frac{1}{2}a\sqrt 5 \)
- C \(\left| {\overrightarrow u } \right| = 3a\sqrt 5 \)
- D \(\left| {\overrightarrow u } \right| = 2a\sqrt 5 \)
Đáp án: A
Phương pháp giải:
Gọi \(O\) là tâm hình vuông. Lấy điểm \(A'\) trên tia \(OA\)sao cho \(OA' = 3OA\). Áp dụng các quy tắc để biến đổi và tính \(\overrightarrow u \).
Lời giải chi tiết:
Gọi \(O\) là tâm hình vuông.
Theo quy tắc ba điểm ta có
\(\begin{array}{l}\overrightarrow u = 4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \\\,\,\,\,\, = 4\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) - 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right) - 2\left( {\overrightarrow {MO} + \overrightarrow {OD} } \right)\\\,\,\,\,\, = 4\overrightarrow {OA} - 3\overrightarrow {OB} + \overrightarrow {OC} - 2\overrightarrow {OD} \end{array}\)
Mà \(\overrightarrow {OD} = - \overrightarrow {OB} ,\,\,\overrightarrow {OC} = - \overrightarrow {OA} \)
\( \Rightarrow \overrightarrow u = 4\overrightarrow {OA} - 3\overrightarrow {OB} + \overrightarrow {OC} - 2\overrightarrow {OD} = 4\overrightarrow {OA} - 3\overrightarrow {OB} - \overrightarrow {OA} + 2\overrightarrow {OB} = 3\overrightarrow {OA} - \overrightarrow {OB} \)
Lấy điểm \(A'\) trên tia \(OA\)sao cho \(OA' = 3OA,\) khi đó: \(\overrightarrow {OA'} = 3\overrightarrow {OA} \)
\( \Rightarrow \overrightarrow u = \overrightarrow {OA'} - \overrightarrow {OB} = \overrightarrow {BA'} .\)
Mặt khác: \(BA' = \sqrt {O{B^2} + OA{'^2}} = \sqrt {O{B^2} + 9O{A^2}} = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + 9.{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = a\sqrt 5 \)
\( \Rightarrow \left| {\overrightarrow u } \right| = BA' = a\sqrt 5 .\)
Chọn A.
Câu hỏi 28 :
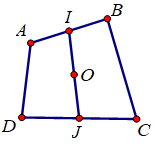
Cho tứ giác \(ABCD\), với M là điểm bất kì. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Khẳng định nào sau đây đúng?
- A \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 3\overrightarrow {MO} \)
- B \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 2\overrightarrow {MO} \)
- C \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MO} \)
- D \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
Đáp án: D
Phương pháp giải:
Áp dụng hệ thức trung điểm để chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \). Từ đó tách để suy ra đpcm.
Lời giải chi tiết:
Theo hệ thức trung điểm ta có \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} ,\,\,\overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {OJ} \)
Mặt khác \(O\) là trung điểm \(IJ \Rightarrow \overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow 0 .\)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 2\left( {\overrightarrow {OI} + \overrightarrow {OJ} } \right) = \overrightarrow 0 .\)
Do đó với mọi điểm \(M\) thì:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \\ \Leftrightarrow \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MC} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MD} } \right) = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} .\end{array}\)
Chọn D.
Câu hỏi 29 :
Cho tam giác \(ABC\) có điểm M thuộc cạnh BC. Chọn khẳng định đúng?
- A \(\overrightarrow {AM} = \frac{{2MC}}{{BC}}\overrightarrow {AB} + \frac{{MB}}{{BC}}\overrightarrow {AC} \)
- B \(\overrightarrow {AM} = \frac{{MC}}{{BC}}\overrightarrow {AB} + \frac{{2MB}}{{BC}}\overrightarrow {AC} \)
- C \(\overrightarrow {AM} = \frac{{MC}}{{BC}}\overrightarrow {AB} - \frac{{MB}}{{BC}}\overrightarrow {AC} \)
- D \(\overrightarrow {AM} = \frac{{MC}}{{BC}}\overrightarrow {AB} + \frac{{MB}}{{BC}}\overrightarrow {AC} \)
Đáp án: D
Phương pháp giải:
Chứng minh \(\frac{{MC}}{{BC}}\overrightarrow {MB} + \frac{{MB}}{{BC}}\overrightarrow {MC} = \overrightarrow 0 \) và \(\frac{{MB}}{{BC}} + \frac{{MC}}{{BC}} = 1\). Áp dụng để biến đổi.
Lời giải chi tiết:
Ta có: \(M \in BC \Rightarrow \overrightarrow {BC} = - \frac{{BC}}{{MB}}\overrightarrow {MB} = \frac{{BC}}{{MC}}\overrightarrow {MC} \Rightarrow \frac{{MC}}{{BC}}\overrightarrow {MB} + \frac{{MB}}{{BC}}\overrightarrow {MC} = \overrightarrow 0 \) và \(\frac{{MB}}{{BC}} + \frac{{MC}}{{BC}} = 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} = \overrightarrow {AM} + \frac{{MC}}{{BC}}\overrightarrow {MB} + \frac{{MB}}{{BC}}\overrightarrow {MC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {AM} \left( {\frac{{MB}}{{BC}} + \frac{{MC}}{{BC}}} \right) + \frac{{MC}}{{BC}}\overrightarrow {MB} + \frac{{MB}}{{BC}}\overrightarrow {MC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{MC}}{{BC}}\left( {\overrightarrow {AM} + \overrightarrow {MB} } \right) + \frac{{MB}}{{BC}}\left( {\overrightarrow {AM} + \overrightarrow {MC} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{MC}}{{BC}}\overrightarrow {AB} + \frac{{MB}}{{BC}}\overrightarrow {AC} .\end{array}\)
Chọn D.
Câu hỏi 30 :
Cho tam giác \(ABC\) đều tâm O. M là điểm tùy ý trong tam giác. Hạ MD, ME, MF tương ứng vuông góc với BC, CA, AB. Chọn khẳng định đúng?
- A \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\overrightarrow {MO} \)
- B \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = 2\overrightarrow {MO} \)
- C \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
- D \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = 3\overrightarrow {MO} \)
Đáp án: C
Phương pháp giải:
Qua M kẻ các đường thẳng song song với các cạnh D ABC. Sử dụng tính chất tam giác đều và quy tắc hình bình hành để biến đổi.
Lời giải chi tiết:
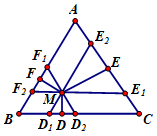
Qua \(M\) kẻ các đường thẳng song song với các cạnh của \(\Delta ABC:\) \({F_1},\,\,{F_2} \in AB;\,\,\,{E_1},\,\,{E_2} \in AC,\,\,\,{D_1},\,\,{D_2} \in BC\) sao cho \({F_1}{D_2}//DC,\,\,{D_1}{E_2}//AB,\,\,\,{F_2}{E_1}//BC.\)
Dễ thấy các tam giác đều \(M{D_1}{D_2},\,\,M{E_1}{E_2},\,\,M{F_1}{F_2}\) và các hình bình hành \(M{F_1}A{E_2},\,\,M{E_1}C{D_2},\,\,M{D_1}B{F_2}\).
Ta có: \(\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{D_1}} + {{\overrightarrow {MD} }_2}} \right),\,\,\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{E_1}} + \overrightarrow {M{E_2}} } \right),\,\,\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{F_1}} + \overrightarrow {M{F_2}} } \right)\)
Cộng từng vế 3 đẳng thức và nhóm ta được:
\(\begin{array}{l}\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{D_1}} + \overrightarrow {M{D_2}} + \overrightarrow {M{E_1}} + \overrightarrow {M{E_2}} + \overrightarrow {M{F_1}} + \overrightarrow {M{F_2}} } \right)\\ = \frac{1}{2}\left[ {\left( {\overrightarrow {M{D_1}} + \overrightarrow {M{F_2}} } \right) + \left( {\overrightarrow {M{F_1}} + \overrightarrow {M{E_2}} } \right) + \left( {\overrightarrow {M{E_1}} + \overrightarrow {M{D_2}} } \right)} \right]\\ = \frac{1}{2}\left( {\overrightarrow {MB} + \overrightarrow {MA} + \overrightarrow {MC} } \right)\\ = \frac{1}{2}.3\overrightarrow {MO} = \frac{3}{2}\overrightarrow {MO} .\end{array}\)
Chọn C.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục