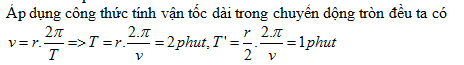Lời giải chi tiết:

Lời giải chi tiết:

Đáp án C

Phương pháp giải:

Phương pháp:

- Tốc độ góc ω = 2πf

- Tốc độ dài: v = ω.r

Lời giải chi tiết:

Cách giải:

Ta có:

  + Tần số f = 400 vòng/phút = \(\frac{{20}}{3}\) vòng/s

  + Bán kính; r = 0,8m

Tốc độ góc của một điểm bất kì ở đầu cánh quạt là: \(\omega  = 2\pi f = 2\pi .\frac{{20}}{3} = 41,87\,rad/s\)

Tốc độ dài của điểm trên đầu cánh quạt là: \(v = r.\omega  = 0,8.41,87{\rm{  = 33,5}}m/s\)

Chọn B

Phương pháp giải:

Phương pháp:

Công thức tính gia tốc hướng tâm  là: \({a_{ht}} = {\omega ^2}r = \frac{{4{\pi ^2}.r}}{{{T^2}}} \Rightarrow T = 2\pi \sqrt {\frac{r}{{{a_{ht}}}}} \)

Lời giải chi tiết:

Cách giải:

Ta có: \({a_{ht}} = {\omega ^2}r = \frac{{4{\pi ^2}.r}}{{{T^2}}} \Rightarrow T = 2\pi \sqrt {\frac{r}{{{a_{ht}}}}}  = 2\pi .\sqrt {\frac{{100}}{4}}  = 10\pi \left( s \right)\)

Chọn D

Phương pháp giải:

Công thức liên hệ giữa tốc độ dài và tốc độ góc: \(\omega  = \dfrac{v}{r}\)

Công thức tính chu kì: \(T = \dfrac{{2\pi }}{\omega }\)

Lời giải chi tiết:

Vệ tinh chuyển động tròn đều với bán kính \(r = R + h = 6400 + 400 = 6800km\), có tâm trùng với tâm Trái Đất.

Ta có tốc độ dài v = 7,820km/s

Tốc độ góc : \(\omega  = \dfrac{v}{r} = \dfrac{{7,82}}{{6800}} = 1,{15.10^{ - 3}}rad/s\)

Chu kì: \(T = \dfrac{{2\pi }}{\omega } \approx 5461s\)

Chọn A

Phương pháp giải:

Chu kì của chuyển động tròn đều là thời gian để vật đi được một vòng.

Công thức liên hệ giữa tần số và chu kì: \(T = \frac{1}{f}\)

Lời giải chi tiết:

Ta có: f = 60 vòng/phút = 1 vòng/s

Chu kì của chuyển động tròn đều là: \(T = \frac{1}{f} = 1s\)

Vậy thời gian để hòn đá quay hết một vòng là 1s

Chọn B

Lời giải chi tiết:

Đáp án A

Áp dụng công thức tính vận tốc dài trong chuyển dộng tròn đều ta có 

Phương pháp giải:

Phương pháp:

Công thức tính gia tốc hướng tâm  là: \({a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r\)

Công thức liên hệ giữa tần số và tốc độ góc: ω = 2πf

Lời giải chi tiết:

Cách giải:

Tần số: f = 5 vòng/phút \( = \frac{1}{{12}}\) vòng/s

Tốc độ góc của chuyển động tròn đều là: \(\omega  = 2\pi .f = 2\pi .\frac{1}{{12}} = \frac{\pi }{6}\,rad/s\)

Gia tốc hướng tâm của em bé đó là: \({a_{ht}} = {\omega ^2}r = {\left( {\frac{\pi }{6}} \right)^2}.3 \approx 0,82m/{s^2}\)

Chọn D

Phương pháp giải:

Công thức liên hệ giữa tốc độ dài và tốc độ góc: \(\omega  = \dfrac{v}{r}\)

Lời giải chi tiết:

A và B có cùng tốc độ góc ω. Gọi r_A ; r_B là bán kính quỹ đạo chuyển động tròn đều của A và B.

Ta có: \({r_A} - {r_B} = 20cm\,\,\,\,\left( 1 \right)\)

Tốc độ dài của A và B là \(\left\{ \begin{array}{l}{v_A} = \omega {r_A} = 60cm/s\\{v_B} = \omega {r_B} = 20cm/s\end{array} \right. \Rightarrow {r_A} = 3{r_B}\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow {r_A} = 30cm \Rightarrow \omega  = \dfrac{{{v_A}}}{{{r_A}}} = \dfrac{{60}}{{30}} = 2rad/s\)

Chọn C

Phương pháp giải:

Tốc độ góc: \(\omega  = \dfrac{{2\pi }}{T}\)

Công thức tính góc quét được trong thời gian ∆t là: \(\alpha  = \omega .\Delta t\)

Lời giải chi tiết:

Tốc độ góc của kim phút và kim giờ: 

\(\left\{ \matrix{
{\omega _{phut}} = {\pi \over {1800}}rad/s = {\omega _1} \hfill \cr
{\omega _{gio}} = {{2\pi } \over {43200}} = {\pi \over {21600}}rad/s = {\omega _2} \hfill \cr} \right.\)

Gọi ∆t là thời gian ngắn nhất từ lúc 15h đến khi hai kim trùng nhau.

Góc kim giờ quét trong ∆t là: \(\alpha  = {\omega _{gio}}\Delta t = {\pi  \over {21600}}.\Delta t\,\,\,\left( {rad} \right)\)

Góc kim phút quét trong ∆t là: \(\beta  = {\omega _{phut}}\Delta t = {\pi  \over {1800}}.\Delta t\,\,\,\left( {rad} \right)\)

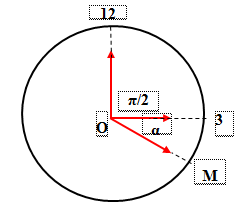
Từ hình vẽ ta có :

\(\beta  - \alpha  = {\pi  \over 2} \Rightarrow {{\pi .\Delta t} \over {1800}} - {{\pi .\Delta t} \over {21600}} = {\pi  \over 2} \Rightarrow \Delta t = 981,82s \approx 16,36phut\)

Chọn A

Phương pháp giải:

Tần số : \(f = \dfrac{1}{T}\)

Chu kì T là thời gian vật quay hết 1 vòng.

Lời giải chi tiết:

Chu kì của kim phút là : \(T = 1h = 3600s\)

Tần số của kim phút là : \(f = \dfrac{1}{T} = \dfrac{1}{{3600}}{s^{ - 1}}\)

Chọn D.

Phương pháp giải:

Công thức tính tốc độ góc: \(\omega  = \dfrac{{2\pi }}{T}\)

Lời giải chi tiết:

R₁ = 15cm; R₂ = 20cm

Chu kì của kim giờ: T₂ = 12h = 43200s

Chu kì của kim phút: T₂ = 1h = 3600s

Tốc độ góc: \(\left\{ \begin{array}{l}{\omega _1} = \dfrac{{2\pi }}{{{T_1}}} \approx 1,{454.10^{ - 4}}\,\,rad/s\\{\omega _2} = \dfrac{{2\pi }}{{{T_2}}} \approx 1,{744.10^{ - 3}}\,\,rad/s\end{array} \right.\)

Lúc 12h hai kim trùng nhau.

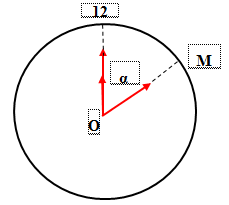
Ta có: \({\alpha _2} - {\alpha _1} = 2\pi  \Leftrightarrow {\omega _2}t - {\omega _1}t = 2\pi  \Rightarrow t = \dfrac{{2\pi }}{{{\omega _2} - {\omega _1}}} \approx 3928s \approx 1h5ph28s\)

Chọn C

Phương pháp giải:

Phương pháp:

Gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r\)

Tốc độ dài: \(v = \omega r = \frac{{2\pi }}{T}.r\)

Lời giải chi tiết:

Cách giải:

Chu kì: T = 90 phút = 5400 s

Có: r = 6380 + 320 = 6700km = 6700 000 m

Vận tốc: \(v = \omega r = \frac{{2\pi }}{T}.r = \frac{{2.3,14}}{{5400}}.6700000 \approx 7792m/s\)

Gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r} = \frac{{{{7792}^2}}}{{6700000}} \approx 9,062m/{s^2}\)

Chọn A

Phương pháp giải:

Phương pháp:

- Công thức liên hệ giữa chu kì và tốc độ góc: \(T = \frac{{2\pi }}{\omega } \Rightarrow \omega  = \frac{{2\pi }}{T}\)

- Công thức liên hệ giữa tốc độ dài và tốc độ góc: v = ωr

Lời giải chi tiết:

Cách giải:

Bán kính của Trái Đất là: R = 6400 km = 6400 000 m

Coi chuyển động của tàu thủy neo tại một điểm trên đường xích đạo là chuyển động tròn đều với bán kính là bán kính Trái Đất và tâm là tâm Trái Đất.

Trái Đất quay quanh trục của nó được một vòng mất 24h  → Chu kì quay của 1 điểm nằm trên đường xích đạo quanh trục Trái Đất là:

T = 24h = 24.3600 = 86400s

Tốc độ góc của tàu đối với trục quay của Trái Đất là:

\(\omega  = \frac{{2\pi }}{T} = \frac{{2.3,14}}{{86400}} = 7,{269.10^{ - 5}}\,rad/s\)

Tốc độ dài của tàu đối với trục quay của Trái Đất là:

\(v = \omega .r = 7,{269.10^{ - 5}}.6400000 = 465,216m/s\)

Chọn B

Phương pháp giải:

Tốc độ góc: v = ωR; R là bán kính của đường tròn

Lời giải chi tiết:

v_A = 50cm/s; v_B = 10cm/s; AB = 20cm.

Ta có: \(\left\{ \begin{array}{l}{v_A} = {R_A}.\omega \\{v_B} = {R_B}.\omega \\{R_A} - {R_B} = AB\end{array} \right. \Rightarrow {v_A} - {v_B} = \left( {{R_A} - {R_B}} \right)\omega  \Rightarrow \omega  = \dfrac{{{v_A} - {v_B}}}{{{R_A} - {R_B}}} = \dfrac{{50 - 10}}{{20}} = 2rad/s\)

\( \Rightarrow \left\{ \begin{array}{l}{R_A} = \dfrac{{{v_A}}}{\omega } = \dfrac{{50}}{2} = 25cm\\{R_B} = \dfrac{{{v_B}}}{\omega } = \dfrac{{10}}{2} = 5cm\end{array} \right.\)

Chọn A