-
Đề thi chính thức tốt nghiệp THPT môn Vật lí
-
Đề thi thử tốt nghiệp THPT môn Vật lí
-
Đề tham khảo thi tốt nghiệp THPT môn Vật lí
- Đề tham khảo thi tốt nghiệp THPT môn Vật lí - Đề số 1
- Đề tham khảo thi tốt nghiệp THPT môn Vật lí - Đề số 2
- Đề tham khảo thi tốt nghiệp THPT môn Vật lí - Đề số 3
- Đề tham khảo thi tốt nghiệp THPT môn Vật lí - Đề số 4
- Đề tham khảo thi tốt nghiệp THPT môn Vật lí - Đề số 5
- Đề tham khảo thi tốt nghiệp THPT môn Vật lí - Đề số 6
Đề tham khảo thi THPT môn Vật lí - Đề số 6 (hay, chi tiết)
Trong điều kiện chuẩn về nhiệt độ và áp suất thì
Đề bài
Trong điều kiện chuẩn về nhiệt độ và áp suất thì
-
A.
số phân tử trong một đơn vị thể tích của các chất khí khác nhau là như nhau.
-
B.
các phân tử của các chất khí khác nhau chuyển động với vận tốc như nhau.
-
C.
khoảng cách giữa các phân tử rất nhỏ so với kích thước của các phân tử.
-
D.
các phân tử khí khác nhau va chạm vào thành bình tác dụng vào thành bình những lực bằng nhau.
Khi truyền nhiệt cho một khối khí thì khối khí có thể
-
A.
tăng nội năng và thực hiện công.
-
B.
giảm nội năng và nhận công.
-
C.
giảm nội năng.
-
D.
nhận công.
Câu nào sau đây nói về nhiệt lượng là không đúng?
-
A.
Nhiệt lượng là số đo độ tăng nội năng của vật trong quá trình truyền nhiệt.
-
B.
Một vật lúc nào cũng có nội năng nên lúc nào cũng có nhiệt lượng.
-
C.
Đơn vị của nhiệt lượng cũng là đơn vị của nội năng.
-
D.
Nhiệt lượng không phải là nội năng.
Phóng xạ là
-
A.
quá trình hạt nhân nguyên tử phát các tia không nhìn thấy.
-
B.
quá trình phân rã tự phát của một hạt nhân không bền vững.
-
C.
quá trình hạt nhân nguyên tử hấp thụ năng lượng để phát ra các tia \(\alpha ,\beta \).
-
D.
quá trình hạt nhân nguyên tử nặng bị phá vỡ thành các hạt nhân nhỏ hơn.
Phát biểu nào sau đây là không đúng khi nói về điện từ trường
-
A.
Khi một điện trường biến thiên theo thời gian, nó sinh ra một từ trường xoáy.
-
B.
Điện trường xoáy là điện trường có các đường sức là những đường cong.
-
C.
Khi một từ trường biến thiên theo thời gian, nó sinh ra một điện trường.
-
D.
Từ trường xoáy có các đường sức từ bao quanh các đường sức điện.
Ban đầu một mẫu chất phóng xạ nguyên chất có \({N_0}\) hạt nhân. Biết chu kì bán rã của chất phóng xạ này là T. Sau thời gian 5T, kể từ thời điểm ban đầu số hạt nhân chưa phân rã của mẫu chất phóng xạ này là
-
A.
\(\frac{{{N_0}}}{{32}}\)
-
B.
\(\frac{{31{N_0}}}{{32}}\)
-
C.
\(\frac{{{N_0}}}{5}\)
-
D.
\(\frac{{{N_0}}}{{10}}\)
Trên hình bên là hai đường đẳng nhiệt của cùng một lượng khí lý tưởng ở hai nhiệt độ khác nhau,
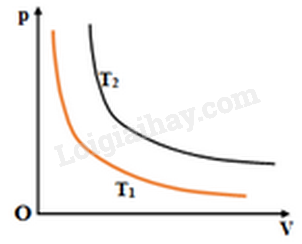
Thông tin đúng khi so sánh nhiệt độ T1 và T2 là
-
A.
\({T_2} > {T_1}.\)
-
B.
\({T_2} = {T_1}.\)
-
C.
\({T_2} < {T_1}.\)
-
D.
\({T_2} \le {T_1}.\)
Trong quá trình truyền sóng điện từ, vector cường độ điện trường \(\overrightarrow E \) và vector cảm ứng từ \(\overrightarrow B \) luôn
-
A.
có phương vuông góc với nhau và vuông góc với phương truyền sóng.
-
B.
có phương song song và cùng chiều.
-
C.
có phương song song và ngược chiều.
-
D.
có phương trùng với phương truyền sóng.
Trong hai nhiệt lượng kế có chứa hai chất lỏng khác nhau ở hai nhiệt độ ban đầu khác nhau. Người ta dùng một nhiệt kế, lần lượt nhúng đi nhúng lại vào nhiệt lượng kế 1 rồi vào nhiệt lượng kế 2. Số chỉ của nhiệt kế lần lượt là 80°C, 16°C, 78°C, 19°C. Đến lần nhúng tiếp theo nhiệt kế chỉ
-
A.
75°C.
-
B.
76°C.
-
C.
77°C.
-
D.
78°C.
Cuộn thứ cấp của một máy biến áp có 800 vòng. Từ thông trong lõi biến thế biến thiên với tần số 50 Hz và giá trị từ thông cực đại qua một vòng dây bằng 2,4 mWb. Suất điện động hiệu dụng cuộn thứ cấp có giá trị xấp xỉ bằng
-
A.
220 V.
-
B.
456,8 V.
-
C.
426,5 V.
-
D.
140 V.
Trong việc truyền tải điện năng đi xa, để giảm công suất tiêu hao trên đường dây \(n\) lần thì cần phải
-
A.
giảm điện áp xuống n lần.
-
B.
giảm điện áp xuống \({n^2}\) lần.
-
C.
tăng điện áp lên n lần.
-
D.
tăng điện áp lên \(\sqrt n \) lần.
Polonium \(_{84}^{210}{P_0}\) phóng xạ \(\alpha \) và biến đổi thành chì Pb. Biết khối lượng các hạt nhân P0; \(\alpha \); Pb lần lượt là: \(209,937303u;\) \(4,001506u;\) \(205,929442u\) và \(1u = 931,5MeV/{c^2}\). Năng lượng tỏa ra khi một hạt nhân Polonium phân rã xấp xỉ bằng
-
A.
\(5,92MeV\).
-
B.
\(2,96MeV\).
-
C.
\(29,60MeV\).
-
D.
\(59,20MeV\).
Để xác định nhiệt hóa hơi của nước người ta làm thí nghiệm sau. Đưa \(10{\rm{ gam}}\)hơi nước ở \({100^0}C\)vào một nhiệt lượng kế chứa \(290{\rm{ gam}}\) nước ở \({20^0}C.\)Nhiệt độ cuối của hệ là \({40^0}C,\)biết nhiệt dung của nhiệt lượng kế là \(46{\rm{ J/K,}}\) nhiệt dung riêng của nước là \(4,18{\rm{ J/g}}{\rm{.K}}.\). Nhiệt hóa hơi của nước là
-
A.
\({\rm{2,02}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
-
B.
\({\rm{2,27}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
-
C.
\({\rm{2,45}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
-
D.
\({\rm{2,68}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
Phát biểu nào sau đây là SAI khi nói về độ phóng xạ (hoạt độ phóng xạ) ?
-
A.
Độ phóng xạ là đại lượng đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ.
-
B.
Đơn vị đo độ phóng xạ là Becquerel \(\left( {Bq} \right).\)
-
C.
Với mỗi lượng chất phóng xạ xác định thì độ phóng xạ tỉ lệ với số nguyên tử của lượng chất đó.
-
D.
Độ phóng xạ của một lượng chất phóng xạ phụ thuộc nhiệt độ của lượng chất đó.
Khi nói về khối lượng phân tử của chất khí \({{\rm{H}}_{\rm{2}}}{\rm{,}}\) \(He,\) \({O_2}\) và \({N_2}\) thì
-
A.
khối lượng phân tử của các khí H2, He,O2 và N2 đều bằng nhau.
-
B.
khối lượng phân tử của O2 nặng nhất trong 4 loại khí trên.
-
C.
khối lượng phân tử của N2 nặng nhất trong 4 loại khí trên.
-
D.
khối lượng phân tử của He nhẹ nhất trong 4 loại khí trên.
Khi ấn từ từ pit tông xuống để nén khí trong xi lanh thì
-
A.
nhiệt độ khí thay đổi.
-
B.
áp suất khí tăng, thể tích khí tăng.
-
C.
áp suất tỉ lệ thuận với thể tích.
-
D.
áp suất khí tăng, thể tích khí giảm.
Hạt nhân X phóng xạ biến đổi thành hạt nhân bên Y. Ban đầu (t = 0) có một mẫu chất X nguyên chất. Tại thời điểm \({t_1}\) và \({t_2}\) tỉ số giữa số hạt nhân Y và số hạt nhân X ở trong mẫu tương ứng là 2 và 3. Tại thời điểm \({t_3} = 2{t_1} + 3{t_2},\)tỉ số đó là
-
A.
17.
-
B.
575.
-
C.
107.
-
D.
72.
Polonium \({}_{84}^{210}{P_0}\)là chất phóng xạ có chu kì bán rã ngày và biến đổi thành hạt nhân chì. Vào lúc \(0\,h\) ngày \(25/1/2024,\) một mẫu phóng xạ có khối lượng \(100{\rm{\;g}}\) được phát hiện, trong đó \(80{\rm{\% }}\) khối lượng của mẫu là chất phóng xạ Polonium \(\;_{84}^{210}{\rm{Po,}}\) phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt \(\alpha \) sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu. Lấy khối lượng của các hạt nhân bằng số khối của chúng tính theo đơn vị \(u.\) Vào ngày nào sau đây khối lượng của mẫu có giá trị là \(99,852\,g\,\,?\)
-
A.
16/2/2024
-
B.
14/2/2024
-
C.
28/4/2024
-
D.
20/12/2024
Một vòng dây kim loại hình tròn đường kính 5 cm được đặt trong vùng từ trường đều có các đường sức từ vuông góc với mặt phẳng vòng dây. Hai đầu của vòng dây được nối với bóng đèn nhỏ tạo thành mạch kín. Lấy \(\pi = 3,14\). Biết điện trở của vòng dây kim loại và bóng đèn lần lượt là \({R_1} = 2\,\Omega \)và \({R_2} = 1{\rm{ }}\Omega \). Tại thời điểm ban đầu (t = 0), người ta bắt đầu thay đổi độ lớn cảm ứng từ theo đồ thị như hình vẽ. Xét tính đúng/sai trong các phát biểu sau:
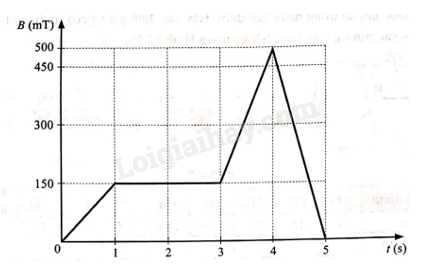
a) Tổng thời gian đèn sáng trong quá trình thay đổi nói trên là 3 s.
b) Suất điện động cảm ứng sinh ra trong khoảng thời gian từ \(t = 0s\)đến \(t = 1s\) là \(1,1775{\rm{ }}mV\).
c) Độ sáng của đèn trong khoảng thời gian từ \(t = 0{\rm{ }}s\)đến \(t = 1{\rm{ }}s\)mạnh hơn trong khoảng thời gian từ \(t = 3\,s\) đến \(t = 4{\rm{ }}s\).
d) Nhiệt lượng tỏa ra trên bóng đèn trong một giây cuối cùng của quá trình thay đổi độ lớn cảm ứng từ xấp xỉ \(1,{1.10^{ - 7}}J\).
Một hạt nhân nguyên tử hydrogen chuyển động với vận tốc v đến va chạm với hạt nhân nguyên tử \(_3^7Li\) đứng yên và bị hạt nhân Lithium bắt giữ. Sau va chạm xuất hiện hai hạt \(\alpha \) bay ra cùng giá trị vận tốc \(v'\). Quỹ đạo của hai hạt \(\alpha \) đối xứng với nhau và hợp với đường nối dài của quỹ đạo hạt prôtôn góc \(\varphi = 80^\circ \). (\({m_p} = 1,007u\); \({m_{He}} = 4,000u\); \({m_{Li}} = 7,000u\), \(u = 1,{66055.10^{ - 27}}kg\)).
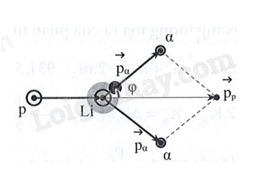
a) Phản ứng hạt nhân là: \({}_1^1p + {}_3^7Li \to 2{}_2^4He\)
b) Phản ứng trên là thu năng lượng
c) Động năng của hạt nhân proton là 2,06 (MeV)
d) Vận tốc v của hạt nhân proton là \({3.10^7}\)(m/s)
Một học sinh đã làm thí nghiệm như sau:
Cho 1 lít nước (coi là 1kg nước) ở 100C vào ấm điện để đun. Theo thời gian học sinh đó ghi được các số liệu sau đây:
- Để đun nóng nước từ 100C đến 1000C cần 18 phút.
- Để cho 200g nước trong ấm hóa hơi khi sôi cần 23 phút.
Bỏ qua nhiệt dung của ấm, biết nhiệt dung riêng của nước là 4,18.103J/(kg.K).
a) Nhiệt lượng cần cung cấp để làm nóng 1 lít nước từ 00C đến 1000C là 376200 J.
b) Công suất của bếp điện là 1045 W.
c) Nhiệt lượng cần cung cấp để hóa hơi 200 g nước ở nhiệt độ sôi là 248700 J.
d) Nhiệt hóa hơi riêng của nước ở 1000C xấp xỉ 2,4.106 J/kg.
Một quả bóng thám không khi ở mặt đất được bơm khí hydrogen áp suất p1 = 105Pa, nhiệt độ 270C. Khi này bóng có bán kính r1 = 1m. Lấy \(\pi = 3,14\).
a) Thể tích quả bóng là V1 = 3m3.
b) Khối lượng hydrogen trong quả bóng là m1 = 0,336kg.
c) Khi lên đến độ cao h, bóng có áp suất là p2 = 0,3.105Pa, nhiệt độ T2 = 200K, coi bóng hoàn toàn đàn hồi, lúc này bóng nở ra có bán kính r2 =1,25m.
d) Động năng trung bình của các phân tử ở mặt đất bằng 1,5 lần ở độ cao h.
Tính nhiệt lượng (theo đơi vị kJ làm tròn đến chữ số thứ nhất sau dấu phẩy) cần cung cấp cho miếng nhôm khối lượng 100 gam ở nhiệt độ 200C, để nó hóa lỏng hoàn toàn ở nhiệt độ 6580C. Biết nhôm có nhiệt dung riêng 896 J/kg.K và nhiệt nóng chảy 39.104 J/kg.
Khối lượng riêng của một chất khí ở áp suất 300 mmHg là 0,3 kg/m3. Vận tốc căn quân phương của các phân tử khí khi đó gần bằng bao nhiêu?
Một hỗn hợp phóng xạ có hai chất phóng xạ X và Y. Biết chu kì bán rã của X và Y lần lượt là \({T_1} = 1h\) và \({T_2} = 2h\), và lúc đầu số hạt X bằng số hạt Y. Tính khoảng thời gian theo đơn vị h để số hạt nguyên chất của hỗn hợp chỉ còn một nửa số hạt lúc đầu. Kết quả làm tròn đến hai chữ số sau dấu phẩy.
Sử dụng các thông tin sau cho 2 câu tiếp theo. Cuộn dây kim loại có điện trở suất \(\rho = {2.10^{ - 8}}\Omega .m\) gồm 1000 vòng được cuốn sát nhau (không chồng lên nhau) tạo thành ống dây hình trụ, đường kính cuộn dây \(d = 10cm\), tiết diện dây 0,2 mm2 có trục song song với \(\overrightarrow B \) của từ trường đều. Tốc độ biến thiên thiên \(\frac{{\Delta B}}{{\Delta t}} = 0,2\left( {\frac{T}{s}} \right)\) Lấy \(\pi = 3,14\)
Điện trở của cuộn dây có giá trị bằng bao nhiêu
Tính độ lớn suất điện động xuất hiện trong khung (Làm tròn kết quả đến chữ số hàng trăm)
Hiện nay Uranium tự nhiên chứa hai đồng vị phóng xạ \(^{235}U\) và \(^{238}U,\) với tỉ lệ số hạt \(^{235}U\)và số hạt \(^{238}U\) là \(\frac{7}{{1000}}.\) Biết chu kì bán rã \(^{235}U\) và \(^{238}U\) lần lượt là \(7,{00.10^8}\) năm và \(4,{50.10^9}\) năm. Cách đây bao nhiêu tỉ năm, Uranium tự nhiên có tỷ lệ số hạt \(^{235}U\) và số \(^{238}U\) là \(\frac{3}{{100}}?\)(Kết quả làm tròn đến 2 chử số thập phân sau dấu phẩy)?
Lời giải và đáp án
Trong điều kiện chuẩn về nhiệt độ và áp suất thì
-
A.
số phân tử trong một đơn vị thể tích của các chất khí khác nhau là như nhau.
-
B.
các phân tử của các chất khí khác nhau chuyển động với vận tốc như nhau.
-
C.
khoảng cách giữa các phân tử rất nhỏ so với kích thước của các phân tử.
-
D.
các phân tử khí khác nhau va chạm vào thành bình tác dụng vào thành bình những lực bằng nhau.
Đáp án : A
Sử dụng định luật khí lý tưởng pV = nRT. Ở cùng nhiệt độ và áp suất, số mol khí trong một thể tích nhất định là như nhau. Theo giả thuyết của thuyết động học phân tử khí, ở cùng điều kiện chuẩn, số phân tử khí trong một đơn vị thể tích là như nhau.
Trong điều kiện chuẩn về nhiệt độ và áp suất (điều kiện tiêu chuẩn áp suất 1 atm, nhiệt độ 273 0 K, thể tích 22,4 lít) thì số phân tử trong một đơn vị thể tích của các chất khí khác nhau là như nhau.
Đáp án: A
Khi truyền nhiệt cho một khối khí thì khối khí có thể
-
A.
tăng nội năng và thực hiện công.
-
B.
giảm nội năng và nhận công.
-
C.
giảm nội năng.
-
D.
nhận công.
Đáp án : A
Sử dụng nguyên lý I nhiệt động lực học \({\rm{\Delta }}U = Q - A\)
Khi truyền nhiệt cho một khối khí thì có thể làm tăng nội năng của khối khí, đồng thời khối khí dãn nở và sinh công.
Ví dụ nhiệt lượng cung cấp cho khối khí trong quá trình đẳng áp, ngoài việc dùng để làm nóng khí (tăng nội năng) còn làm cho chất khí dãn nở (khí thực hiện công).
Đáp án: A
Câu nào sau đây nói về nhiệt lượng là không đúng?
-
A.
Nhiệt lượng là số đo độ tăng nội năng của vật trong quá trình truyền nhiệt.
-
B.
Một vật lúc nào cũng có nội năng nên lúc nào cũng có nhiệt lượng.
-
C.
Đơn vị của nhiệt lượng cũng là đơn vị của nội năng.
-
D.
Nhiệt lượng không phải là nội năng.
Đáp án : B
Nhiệt lượng là số đo độ biến thiên nội năng trong quá trình truyền nhiệt. Một vật lúc nào cũng có nội năng nhưng không có nghĩa là lúc nào cũng có nhiệt lượng, vì nhiệt lượng chỉ xuất hiện khi có sự trao đổi nhiệt.
Nhiệt lượng là số đo độ biến thiên nội năng của vật trong quá trình truyền nhiệt.
Một vật lúc nào cũng có nội năng nhưng không tham gia vào quá trình truyền nhiệt thì nội năng không biến đổi nên không có nhiệt lượng được nhận thêm hay mất đi.
Đáp án: B
Phóng xạ là
-
A.
quá trình hạt nhân nguyên tử phát các tia không nhìn thấy.
-
B.
quá trình phân rã tự phát của một hạt nhân không bền vững.
-
C.
quá trình hạt nhân nguyên tử hấp thụ năng lượng để phát ra các tia \(\alpha ,\beta \).
-
D.
quá trình hạt nhân nguyên tử nặng bị phá vỡ thành các hạt nhân nhỏ hơn.
Đáp án : B
Phóng xạ là quá trình một hạt nhân không bền tự phát phân rã thành hạt nhân khác và phát ra bức xạ. Không cần hấp thụ năng lượng bên ngoài.
- Phóng xạ là hiện tượng hạt nhân nguyên tử của một số nguyên tố (kém bền vững) tự phóng ra các bức xạ rồi biến đổi thành hạt nhân nguyên tử của các nguyên tố khác (bền vững hơn).
- Như vậy phóng xạ quá trình phân rã tự phát của một hạt nhân không bền vững.
Đáp án: B
Phát biểu nào sau đây là không đúng khi nói về điện từ trường
-
A.
Khi một điện trường biến thiên theo thời gian, nó sinh ra một từ trường xoáy.
-
B.
Điện trường xoáy là điện trường có các đường sức là những đường cong.
-
C.
Khi một từ trường biến thiên theo thời gian, nó sinh ra một điện trường.
-
D.
Từ trường xoáy có các đường sức từ bao quanh các đường sức điện.
Đáp án : B
Khi một điện trường biến thiên theo thời gian, nó sinh ra một từ trường xoáy. Điện trường xoáy có các đường sức là đường cong kín, không chỉ là đường cong.
Điện trường xoáy có các đường sức là những đường cong kín, không phải chỉ là những đường cong.
Đáp án: B
Ban đầu một mẫu chất phóng xạ nguyên chất có \({N_0}\) hạt nhân. Biết chu kì bán rã của chất phóng xạ này là T. Sau thời gian 5T, kể từ thời điểm ban đầu số hạt nhân chưa phân rã của mẫu chất phóng xạ này là
-
A.
\(\frac{{{N_0}}}{{32}}\)
-
B.
\(\frac{{31{N_0}}}{{32}}\)
-
C.
\(\frac{{{N_0}}}{5}\)
-
D.
\(\frac{{{N_0}}}{{10}}\)
Đáp án : A
Công thức phân rã phóng xạ \(N = {N_0}.{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\)
\(N = {N_0}{.2^{\frac{{ - t}}{T}}} = {N_0}{.2^{ - 5}} = \frac{{{N_0}}}{{32}}\)
Đáp án: A
Trên hình bên là hai đường đẳng nhiệt của cùng một lượng khí lý tưởng ở hai nhiệt độ khác nhau,
Thông tin đúng khi so sánh nhiệt độ T1 và T2 là
-
A.
\({T_2} > {T_1}.\)
-
B.
\({T_2} = {T_1}.\)
-
C.
\({T_2} < {T_1}.\)
-
D.
\({T_2} \le {T_1}.\)
Đáp án : A
Trên đồ thị đẳng nhiệt, đường nằm trên ứng với nhiệt độ cao hơn. Sử dụng phương trình trạng thái khí lý tưởng để so sánh vận tốc phân tử khí.
\({T_2} > {T_1}\)do Từ \({V_o}\) kẻ đường thẳng song song với trục Op, cắt hai đường đẳng nhiệt tại hai vị trí (1) và (2) . Khi đó ta có \({p_2} > {p_1}\)nên các phân tử chất khí ở trạng thái (2) chuyển động nhanh hơn các phân tử chất khí ở trạng thái (1) nên \({T_2} > {T_1}.\)
Đáp án: A
Trong quá trình truyền sóng điện từ, vector cường độ điện trường \(\overrightarrow E \) và vector cảm ứng từ \(\overrightarrow B \) luôn
-
A.
có phương vuông góc với nhau và vuông góc với phương truyền sóng.
-
B.
có phương song song và cùng chiều.
-
C.
có phương song song và ngược chiều.
-
D.
có phương trùng với phương truyền sóng.
Đáp án : A
Trong sóng điện từ: E vuông góc với B, cả hai vuông góc với phương truyền sóng.
Trong quá trình truyền sóng điện từ, vector cường độ điện trường \(\overrightarrow E \) và vector cảm ứng từ \(\overrightarrow B \) luôn có phương vuông góc với nhau và vuông góc với phương truyền sóng
Đáp án: A
Trong hai nhiệt lượng kế có chứa hai chất lỏng khác nhau ở hai nhiệt độ ban đầu khác nhau. Người ta dùng một nhiệt kế, lần lượt nhúng đi nhúng lại vào nhiệt lượng kế 1 rồi vào nhiệt lượng kế 2. Số chỉ của nhiệt kế lần lượt là 80°C, 16°C, 78°C, 19°C. Đến lần nhúng tiếp theo nhiệt kế chỉ
-
A.
75°C.
-
B.
76°C.
-
C.
77°C.
-
D.
78°C.
Đáp án : B
Nhiệt kế trao đổi nhiệt với các chất lỏng theo phương trình cân bằng nhiệt. Dựa vào quy luật trung bình cộng dần của nhiệt độ trong quá trình truyền nhiệt
Gọi nhiệt dung của bình 1,2 và nhiệt kế lần lượt là c1, c2, c3.
Khi nhúng nhiệt kế vào bình 1 thì nhiệt độ cân bằng là \({78^ \circ }C\) ta có \({c_3}\left( {78 - 16} \right) = {c_1}\left( {80 - 78} \right) \Rightarrow {c_1} = 31{c_3}\)
Khi nhúng nhiệt kế vào bình 2 thì nhiệt độ cân bằng là \({19^ \circ }C\) ta có \({c_3}\left( {78 - 19} \right) = {c_2}\left( {19 - 16} \right) \Rightarrow {c_2} = \frac{{59}}{3}{c_3}\)
Đến lần nhúng tiếp theo vào bình 1 thì
\({t_5} = \frac{{{c_1}.78 + {c_3}.19}}{{{c_1} + {c_3}}} = \frac{{31.78 + 1.19}}{{31 + 1}} = \frac{{2437}}{{32}} \approx {76^ \circ }C.\)
Đáp án: B
Cuộn thứ cấp của một máy biến áp có 800 vòng. Từ thông trong lõi biến thế biến thiên với tần số 50 Hz và giá trị từ thông cực đại qua một vòng dây bằng 2,4 mWb. Suất điện động hiệu dụng cuộn thứ cấp có giá trị xấp xỉ bằng
-
A.
220 V.
-
B.
456,8 V.
-
C.
426,5 V.
-
D.
140 V.
Đáp án : C
Công thức suất điện động cảm ứng: \(e = - N\frac{{\Delta \Phi }}{{\Delta t}} = 2\pi fN{\Phi _0}\sin \omega t\)
Do cấu tạo của máy biến áp, hầu như mọi đường sức từ chỉ chạy trong lõi biến áp nên từ thông qua mỗi vòng dây ở cả hai cuộn bằng nhau, suất điện động cảm ứng trong mỗi vòng dây cũng bằng nhau.
Suất điện động ở cuộn thứ cấp là: \({e_{c2}} = - {N_2}\frac{{\Delta \Phi }}{{\Delta t}} = 2\pi f{N_2}{\Phi _0} \cdot \sin \omega t\)
Suất điện động hiệu dụng cuộn thứ cấp là:
\({E_2} = \frac{{{E_0}}}{{\sqrt 2 }} = \frac{{2\pi f{N_2}{\Phi _0}}}{{\sqrt 2 }} = \frac{{2\pi \cdot 50 \cdot 800 \cdot 2,4 \cdot {{10}^{ - 3}}}}{{\sqrt 2 }} \simeq 426,5\,\,V\)
Đáp án: C
Trong việc truyền tải điện năng đi xa, để giảm công suất tiêu hao trên đường dây \(n\) lần thì cần phải
-
A.
giảm điện áp xuống n lần.
-
B.
giảm điện áp xuống \({n^2}\) lần.
-
C.
tăng điện áp lên n lần.
-
D.
tăng điện áp lên \(\sqrt n \) lần.
Đáp án : D
Công suất hao phí trên đường dây \({P_{hp}} = {I^2}r\)
Hao phí trên đường dây tải điện được xác định bằng biểu thức: \({P_{hp}} = {I^2}r = \frac{{{P^2}}}{{{U^2}{{\cos }^2}\varphi }}r \Rightarrow {P_{hp}} \sim \frac{1}{{{U^2}}}\)
Nên để \({P_{hp}}\) giảm đi n lần thì U tăng lên \(\sqrt n \)
Đáp án: D
Polonium \(_{84}^{210}{P_0}\) phóng xạ \(\alpha \) và biến đổi thành chì Pb. Biết khối lượng các hạt nhân P0; \(\alpha \); Pb lần lượt là: \(209,937303u;\) \(4,001506u;\) \(205,929442u\) và \(1u = 931,5MeV/{c^2}\). Năng lượng tỏa ra khi một hạt nhân Polonium phân rã xấp xỉ bằng
-
A.
\(5,92MeV\).
-
B.
\(2,96MeV\).
-
C.
\(29,60MeV\).
-
D.
\(59,20MeV\).
Đáp án : A
Công thức năng lượng tỏa ra \({\rm{\Delta }}E = {\rm{\Delta }}m{c^2}\)
∆E = (mPo - mα – mX)c2 = 5,92 MeV
Đáp án: A
Để xác định nhiệt hóa hơi của nước người ta làm thí nghiệm sau. Đưa \(10{\rm{ gam}}\)hơi nước ở \({100^0}C\)vào một nhiệt lượng kế chứa \(290{\rm{ gam}}\) nước ở \({20^0}C.\)Nhiệt độ cuối của hệ là \({40^0}C,\)biết nhiệt dung của nhiệt lượng kế là \(46{\rm{ J/K,}}\) nhiệt dung riêng của nước là \(4,18{\rm{ J/g}}{\rm{.K}}.\). Nhiệt hóa hơi của nước là
-
A.
\({\rm{2,02}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
-
B.
\({\rm{2,27}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
-
C.
\({\rm{2,45}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
-
D.
\({\rm{2,68}}{\rm{.1}}{{\rm{0}}^{\rm{3}}}{\rm{ kJ/kg}}{\rm{.}}\)
Đáp án : B
Áp dụng phương trình cân bằng nhiệt giữa hơi nước ngưng tụ và nước trong nhiệt lượng kế. Giải phương trình để tìm nhiệt hóa hơi.
Ta có \(\left\{ \begin{array}{l}{Q_{thu}} = L{m_h} + {m_h}c\Delta t = 0,01.L + 0,01.4180.\left( {100 - 40} \right)\\{Q_{toa}} = {m_n}c\Delta t' + 46.\Delta t' = 0,29.4180.\left( {40 - 20} \right) + 46.\left( {40 - 20} \right) = 25164{\rm{ J}}.\end{array} \right.\)
\({Q_{thu}} = {Q_{toa}}0,01L + 2508 = 25164 \Rightarrow L = 2,{27.10^{\rm{6}}}{\rm{ J/kg}} = 2,{27.10^3}{\rm{ }}k{\rm{J/}}kg.\)
Đáp án: B
Phát biểu nào sau đây là SAI khi nói về độ phóng xạ (hoạt độ phóng xạ) ?
-
A.
Độ phóng xạ là đại lượng đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ.
-
B.
Đơn vị đo độ phóng xạ là Becquerel \(\left( {Bq} \right).\)
-
C.
Với mỗi lượng chất phóng xạ xác định thì độ phóng xạ tỉ lệ với số nguyên tử của lượng chất đó.
-
D.
Độ phóng xạ của một lượng chất phóng xạ phụ thuộc nhiệt độ của lượng chất đó.
Đáp án : D
Độ phóng xạ chỉ phụ thuộc vào số hạt nhân phóng xạ và không bị ảnh hưởng bởi nhiệt độ.
Để đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ, người ta dùng đại lượng độ phóng xạ (hay hoạt độ phóng xạ), kí hiệu là H, có giá trị bằng số hạt nhân phân rã trong một giây.
Đơn vị đo độ phóng xạ là Becquerel, kí hiệu là \(Bq.\)
\(1\,Bq = \)1 phân rã / 1 giây.
Trong thực tế, độ phóng xạ còn được đo bằng đơn vị Curie, kí hiệu là \(Ci.\)
\(1\,Ci = 3,7 \cdot {10^{10}}\,Bq.\)
Độ phóng xạ \({H_t} = \lambda \cdot {N_t},\) với \(\lambda = \frac{{\ln 2}}{T}\) là hằng số phóng xạ \( \Rightarrow {H_t} \sim {N_t}.\)
Đáp án: D
Khi nói về khối lượng phân tử của chất khí \({{\rm{H}}_{\rm{2}}}{\rm{,}}\) \(He,\) \({O_2}\) và \({N_2}\) thì
-
A.
khối lượng phân tử của các khí H2, He,O2 và N2 đều bằng nhau.
-
B.
khối lượng phân tử của O2 nặng nhất trong 4 loại khí trên.
-
C.
khối lượng phân tử của N2 nặng nhất trong 4 loại khí trên.
-
D.
khối lượng phân tử của He nhẹ nhất trong 4 loại khí trên.
Đáp án : B
Tính khối lượng mol của từng chất
Khối lượng phân tử của \({H_2}\) là \({\rm{2 g/mol}}{\rm{.}}\)
Khối lượng phân tử của \(He\)là \({\rm{4 g/mol}}{\rm{.}}\)
Khối lượng phân tử của \({O_2}\) là \({\rm{32 g/mol}}{\rm{.}}\)
Khối lượng phân tử của \({N_2}\) là \({\rm{28 g/mol}}{\rm{.}}\)
Vậy khối lượng phân tử của \({O_2}\) nặng nhất trong 4 loại khí trên.
Đáp án: B
Khi ấn từ từ pit tông xuống để nén khí trong xi lanh thì
-
A.
nhiệt độ khí thay đổi.
-
B.
áp suất khí tăng, thể tích khí tăng.
-
C.
áp suất tỉ lệ thuận với thể tích.
-
D.
áp suất khí tăng, thể tích khí giảm.
Đáp án : D
Định luật Boyle-Mariotte: pV = const
Trường hợp thỏa mãn quá trình đẳng nhiệt khi pit tông nén từ từ.
Đáp án: D
Hạt nhân X phóng xạ biến đổi thành hạt nhân bên Y. Ban đầu (t = 0) có một mẫu chất X nguyên chất. Tại thời điểm \({t_1}\) và \({t_2}\) tỉ số giữa số hạt nhân Y và số hạt nhân X ở trong mẫu tương ứng là 2 và 3. Tại thời điểm \({t_3} = 2{t_1} + 3{t_2},\)tỉ số đó là
-
A.
17.
-
B.
575.
-
C.
107.
-
D.
72.
Đáp án : B
Áp dụng công thức số hạt nhân phân rã. Sử dụng bảng giá trị đã tính trước để suy ra kết quả.
Phương trình phóng xạ: \(X \to Y + \)tia phóng xạ.
Tại \({t_1}\), tỉ số giữa số hạt nhân con và hạt nhân mẹ là: \(\frac{{{N_Y}}}{{{N_X}}} = 2 = {2^{\frac{{{t_1}}}{T}}} - 1 \Rightarrow {2^{\frac{{{t_1}}}{T}}} = 3 \Rightarrow \frac{{{t_1}}}{T} = \ell o{g_2}3\)
Tại \({t_2}\), tỉ số giữa số hạt nhân con và hạt nhân mẹ là:
\(\frac{{{N_Y}}}{{{N_X}}} = 3 = {2^{\frac{{{t_2}}}{T}}} - 1 \Rightarrow {2^{\frac{{{t_2}}}{T}}} = 4 \Rightarrow \frac{{{t_2}}}{T} = \ell o{g_2}4 = 2\)
Tại \({t_3}\), tỉ số giữa số hạt nhân con và hạt nhân mẹ là:
\(\frac{{{N_Y}}}{{{N_X}}} = {2^{\frac{{2{t_1} + 3{t_2}}}{T}}} - 1 \Rightarrow {2^{2\frac{{{t_1}}}{T} + 3\frac{{{t_2}}}{T}}} - 1 = {2^{2\ell o{g_2}3.2}} - 1 = 575\)
Đáp án: B
Polonium \({}_{84}^{210}{P_0}\)là chất phóng xạ có chu kì bán rã ngày và biến đổi thành hạt nhân chì. Vào lúc \(0\,h\) ngày \(25/1/2024,\) một mẫu phóng xạ có khối lượng \(100{\rm{\;g}}\) được phát hiện, trong đó \(80{\rm{\% }}\) khối lượng của mẫu là chất phóng xạ Polonium \(\;_{84}^{210}{\rm{Po,}}\) phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt \(\alpha \) sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu. Lấy khối lượng của các hạt nhân bằng số khối của chúng tính theo đơn vị \(u.\) Vào ngày nào sau đây khối lượng của mẫu có giá trị là \(99,852\,g\,\,?\)
-
A.
16/2/2024
-
B.
14/2/2024
-
C.
28/4/2024
-
D.
20/12/2024
Đáp án : B
Áp dụng công thức chu kỳ bán rã để tính thời gian cần thiết. Xác định ngày dựa trên kết quả tính toán.
\(_{81}^{210}Po \to _2^4\alpha + _{82}^{206}Pb\)
\({m_\alpha } = 100 - 99,852 = 0,148\,g.\)
\(\Delta N = {N_0}\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \frac{{{m_\alpha }}}{{{A_\alpha }}} = \frac{{{m_{Po}}}}{{{A_{Po}}}}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \frac{{0,148}}{4} = \frac{{100.0,8}}{{210}}.\left( {1 - {2^{\frac{{ - t}}{{138}}}}} \right) \Rightarrow t \simeq 20ng\`a y\)
Khối lượng của mẫu có giá trị là \(99,852\,g\,\,\)vào ngày \(14/2/2024.\)
Đáp án: B
Một vòng dây kim loại hình tròn đường kính 5 cm được đặt trong vùng từ trường đều có các đường sức từ vuông góc với mặt phẳng vòng dây. Hai đầu của vòng dây được nối với bóng đèn nhỏ tạo thành mạch kín. Lấy \(\pi = 3,14\). Biết điện trở của vòng dây kim loại và bóng đèn lần lượt là \({R_1} = 2\,\Omega \)và \({R_2} = 1{\rm{ }}\Omega \). Tại thời điểm ban đầu (t = 0), người ta bắt đầu thay đổi độ lớn cảm ứng từ theo đồ thị như hình vẽ. Xét tính đúng/sai trong các phát biểu sau:
a) Tổng thời gian đèn sáng trong quá trình thay đổi nói trên là 3 s.
b) Suất điện động cảm ứng sinh ra trong khoảng thời gian từ \(t = 0s\)đến \(t = 1s\) là \(1,1775{\rm{ }}mV\).
c) Độ sáng của đèn trong khoảng thời gian từ \(t = 0{\rm{ }}s\)đến \(t = 1{\rm{ }}s\)mạnh hơn trong khoảng thời gian từ \(t = 3\,s\) đến \(t = 4{\rm{ }}s\).
d) Nhiệt lượng tỏa ra trên bóng đèn trong một giây cuối cùng của quá trình thay đổi độ lớn cảm ứng từ xấp xỉ \(1,{1.10^{ - 7}}J\).
a) Tổng thời gian đèn sáng trong quá trình thay đổi nói trên là 3 s.
b) Suất điện động cảm ứng sinh ra trong khoảng thời gian từ \(t = 0s\)đến \(t = 1s\) là \(1,1775{\rm{ }}mV\).
c) Độ sáng của đèn trong khoảng thời gian từ \(t = 0{\rm{ }}s\)đến \(t = 1{\rm{ }}s\)mạnh hơn trong khoảng thời gian từ \(t = 3\,s\) đến \(t = 4{\rm{ }}s\).
d) Nhiệt lượng tỏa ra trên bóng đèn trong một giây cuối cùng của quá trình thay đổi độ lớn cảm ứng từ xấp xỉ \(1,{1.10^{ - 7}}J\).
Sử dụng công thức suất điện động cảm ứng \({e_c} = N\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = NS\left| {\frac{{\Delta B}}{{\Delta t}}} \right|\)
Xác định tổng thời gian đèn sáng từ đồ thị.
Sử dụng công suất \(P = \frac{{{e^2}}}{R}\) và tính nhiệt lượng Q =Pt
a. Từ đồ thị ta thấy tổng thời gian cảm ứng từ biến thiên là 3s, tổng thời gian này cũng là tổng thời gian đèn sáng. ⟹ Đ
b. Độ lớn suất điện động trong khoảng thời gian t = 0s đến t = 1 s là:
\({e_c} = N\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = NS\left| {\frac{{\Delta B}}{{\Delta t}}} \right| = 1.\frac{{3,14.0,{{05}^2}}}{4}\left| {\frac{{{{150.10}^{ - 3}} - 0}}{{1 - 0}}} \right| = 2,{94.10^{ - 4}}V\) ⟹ S
c. Căn cứ vào độ dốc của đồ thị, ta thấy độ sáng của đèn từ 0 s đến 1 s yếu hơn trong khoảng thời gian từ 3 s đến 4 s. ⟹ S
d. Độ lớn suất điện động trong khoảng thời gian \(t = 4s\) đến \(t = 5s\) là:
\({e_c} = N\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = NS\left| {\frac{{\Delta B}}{{\Delta t}}} \right| = 1.\frac{{3,14.0,{{05}^2}}}{4}\left| {\frac{{0 - {{500.10}^{ - 3}}}}{{5 - 4}}} \right| = 9,{8125.10^{ - 4}}V\)
* Nhiệt lượng tỏa ra trên bóng đèn: \({P_2} = {R_2}{I^2} = {R_2}{\left( {\frac{{{e_c}}}{{{R_1} + {R_2}}}} \right)^2} = 1.{\left( {\frac{{9,{{8125.10}^{ - 4}}}}{{2 + 1}}} \right)^2} \approx 1,{1.10^{ - 7}}W\)
⟹ Đ
Một hạt nhân nguyên tử hydrogen chuyển động với vận tốc v đến va chạm với hạt nhân nguyên tử \(_3^7Li\) đứng yên và bị hạt nhân Lithium bắt giữ. Sau va chạm xuất hiện hai hạt \(\alpha \) bay ra cùng giá trị vận tốc \(v'\). Quỹ đạo của hai hạt \(\alpha \) đối xứng với nhau và hợp với đường nối dài của quỹ đạo hạt prôtôn góc \(\varphi = 80^\circ \). (\({m_p} = 1,007u\); \({m_{He}} = 4,000u\); \({m_{Li}} = 7,000u\), \(u = 1,{66055.10^{ - 27}}kg\)).
a) Phản ứng hạt nhân là: \({}_1^1p + {}_3^7Li \to 2{}_2^4He\)
b) Phản ứng trên là thu năng lượng
c) Động năng của hạt nhân proton là 2,06 (MeV)
d) Vận tốc v của hạt nhân proton là \({3.10^7}\)(m/s)
a) Phản ứng hạt nhân là: \({}_1^1p + {}_3^7Li \to 2{}_2^4He\)
b) Phản ứng trên là thu năng lượng
c) Động năng của hạt nhân proton là 2,06 (MeV)
d) Vận tốc v của hạt nhân proton là \({3.10^7}\)(m/s)
Áp dụng định luật bảo toàn năng lượng và động lượng.
Sử dụng công thức tính động năng \(K = \frac{1}{2}m{v^2}\)
Xác định năng lượng phản ứng \(\Delta E = {\rm{\Delta }}m \cdot {c^2}\)
a. Phản ứng hạt nhân: \({}_1^1p + {}_3^7Li \to 2{}_2^4He\) ⟹ Đ
b. Ta có năng lượng của phản ứng:
\(\Delta E = \left( {{m_p} + {m_{Li}} - 2.{m_\alpha }} \right).931,5 = 6,5205\left( {MeV} \right)\)> 0 Vậy phản ứng toả năng lượng. ⟹ S
c. Ta có: \(2.{K_\alpha } - {K_p} = \Delta E = 6,5205\) (1)
Ta lại có: \(\cos {80^0} = \frac{{{p_p}}}{{2.{p_\alpha }}} \Rightarrow \frac{{p_p^2}}{{p_\alpha ^2}} = 0,12\)
\( \Rightarrow {K_p} = 4.{K_\alpha }.0,12\) (2)
Từ (1) và (2) \( \Rightarrow {K_\alpha } = 4,29\left( {MeV} \right);{K_p} = 2,06\left( {MeV} \right)\) ⟹ Đ
d. Vận tốc của proton là: \({K_p} = 2,06\left( {MeV} \right) = \frac{1}{2}.1.931,5\frac{{MeV}}{{{c^2}}}.{v^2} \Rightarrow v = {2.10^7}\left( {{m \mathord{\left/
{\vphantom {m s}} \right.
\kern-\nulldelimiterspace} s}} \right)\) ⟹ S
Một học sinh đã làm thí nghiệm như sau:
Cho 1 lít nước (coi là 1kg nước) ở 100C vào ấm điện để đun. Theo thời gian học sinh đó ghi được các số liệu sau đây:
- Để đun nóng nước từ 100C đến 1000C cần 18 phút.
- Để cho 200g nước trong ấm hóa hơi khi sôi cần 23 phút.
Bỏ qua nhiệt dung của ấm, biết nhiệt dung riêng của nước là 4,18.103J/(kg.K).
a) Nhiệt lượng cần cung cấp để làm nóng 1 lít nước từ 00C đến 1000C là 376200 J.
b) Công suất của bếp điện là 1045 W.
c) Nhiệt lượng cần cung cấp để hóa hơi 200 g nước ở nhiệt độ sôi là 248700 J.
d) Nhiệt hóa hơi riêng của nước ở 1000C xấp xỉ 2,4.106 J/kg.
a) Nhiệt lượng cần cung cấp để làm nóng 1 lít nước từ 00C đến 1000C là 376200 J.
b) Công suất của bếp điện là 1045 W.
c) Nhiệt lượng cần cung cấp để hóa hơi 200 g nước ở nhiệt độ sôi là 248700 J.
d) Nhiệt hóa hơi riêng của nước ở 1000C xấp xỉ 2,4.106 J/kg.
Nhiệt lượng để đun nóng nước: \(Q = mc{\rm{\Delta }}T\)
Công suất của bếp điện: \(P = \frac{Q}{t}\)
Nhiệt lượng hóa hơi \(Q = mL\)
a) \(Q = mc\Delta t = 1.4,{18.10^3}.90 = 376200J\) → Đúng
b) \(P = \frac{Q}{t} = \frac{{376200}}{{18.60}} = 384,3W\) → Sai
c) \(Q' = Pt' = 384,3.23.60 = 480654J\) → Sai
d) \(L = \frac{{Q'}}{{m'}} = \frac{{480654}}{{0,2}} \approx {2.4.10^6}J/kg\) → Đúng
Một quả bóng thám không khi ở mặt đất được bơm khí hydrogen áp suất p1 = 105Pa, nhiệt độ 270C. Khi này bóng có bán kính r1 = 1m. Lấy \(\pi = 3,14\).
a) Thể tích quả bóng là V1 = 3m3.
b) Khối lượng hydrogen trong quả bóng là m1 = 0,336kg.
c) Khi lên đến độ cao h, bóng có áp suất là p2 = 0,3.105Pa, nhiệt độ T2 = 200K, coi bóng hoàn toàn đàn hồi, lúc này bóng nở ra có bán kính r2 =1,25m.
d) Động năng trung bình của các phân tử ở mặt đất bằng 1,5 lần ở độ cao h.
a) Thể tích quả bóng là V1 = 3m3.
b) Khối lượng hydrogen trong quả bóng là m1 = 0,336kg.
c) Khi lên đến độ cao h, bóng có áp suất là p2 = 0,3.105Pa, nhiệt độ T2 = 200K, coi bóng hoàn toàn đàn hồi, lúc này bóng nở ra có bán kính r2 =1,25m.
d) Động năng trung bình của các phân tử ở mặt đất bằng 1,5 lần ở độ cao h.
Sử dụng phương trình khí lý tưởng pV = nRT
Thể tích bóng theo công thức hình cầu \(V = \frac{4}{3}\pi {r^3}\)
Xác định khối lượng hydro từ khối lượng mol \(m = nM\)
Động năng trung bình \(E = \frac{3}{2}kT\)
a. \({V_1} = \frac{4}{3}\pi r_1^3 = \frac{4}{3}\pi {.1^3} = 4,187{m^3}.\) → Sai
b. \({p_1}{V_1} = \frac{{{m_1}}}{M}RT \Rightarrow {m_1} = \frac{{{p_1}{V_1}M}}{{kT}} = \frac{{{{10}^5}.4,{{187.2.10}^{ - 3}}}}{{8,31.300}} = 0,336kg\) → Đúng
c. \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Leftrightarrow \frac{{{p_1}\frac{4}{3}\pi r_1^3}}{{{T_1}}} = \frac{{{p_2}\frac{4}{3}\pi r_2^3}}{{{T_2}}} \Rightarrow {r_2} = \sqrt(3){{\frac{{{p_1}r_1^3{T_2}}}{{{p_2}{T_1}}}}} = \sqrt(3){{\frac{{{{10}^5}{{.1}^3}.200}}{{0,{{3.10}^5}.300}}}} = 1,305m\) → Sai
d. \(\frac{{\overline {{E_{d1}}} }}{{\overline {{E_{d2}}} }} = \frac{{{T_1}}}{{{T_2}}} = \frac{{300}}{{200}} = 1,5\) → Đúng
Tính nhiệt lượng (theo đơi vị kJ làm tròn đến chữ số thứ nhất sau dấu phẩy) cần cung cấp cho miếng nhôm khối lượng 100 gam ở nhiệt độ 200C, để nó hóa lỏng hoàn toàn ở nhiệt độ 6580C. Biết nhôm có nhiệt dung riêng 896 J/kg.K và nhiệt nóng chảy 39.104 J/kg.
Nhiệt lượng cần cung cấp Q = cm(t2 – t1) + \(\lambda m\)
Nhiệt lượng cần cung cấp Q = cm(t2 – t1) + \(\lambda m\) = 96165 J ≈ 96,2 kJ
Đáp án: 96,2
Khối lượng riêng của một chất khí ở áp suất 300 mmHg là 0,3 kg/m3. Vận tốc căn quân phương của các phân tử khí khi đó gần bằng bao nhiêu?
Sử dụng công thức: \(p = \frac{1}{3}Dv_c^2\)
Ta có \(p = \frac{1}{3}Dv_c^2 \Rightarrow 300.\frac{{101325}}{{760}} = \frac{1}{3}.0,3.v_c^2 \Rightarrow {v_c} \approx 63{\rm{0 m/s}}.\)
Đáp án: 630
Một hỗn hợp phóng xạ có hai chất phóng xạ X và Y. Biết chu kì bán rã của X và Y lần lượt là \({T_1} = 1h\) và \({T_2} = 2h\), và lúc đầu số hạt X bằng số hạt Y. Tính khoảng thời gian theo đơn vị h để số hạt nguyên chất của hỗn hợp chỉ còn một nửa số hạt lúc đầu. Kết quả làm tròn đến hai chữ số sau dấu phẩy.
Số hạt còn lại của mỗi chất phóng xạ tuân theo công thức: \(N = {N_0}{e^{ - \lambda t}}\)
\({N_X} + {N_Y} = \frac{{{N_0} + {N_0}}}{2} \Leftrightarrow {N_0}{e^{ - \frac{{\ln 2}}{T}t}} + {N_0}{e^{ - \frac{{\ln 2}}{{2T}}t}} = {N_0} \Rightarrow {e^{ - \frac{{\ln 2}}{T}t}} \approx 0,618 \Rightarrow t \approx 1,39\,h\).
Đáp án: 1,39
Sử dụng các thông tin sau cho 2 câu tiếp theo. Cuộn dây kim loại có điện trở suất \(\rho = {2.10^{ - 8}}\Omega .m\) gồm 1000 vòng được cuốn sát nhau (không chồng lên nhau) tạo thành ống dây hình trụ, đường kính cuộn dây \(d = 10cm\), tiết diện dây 0,2 mm2 có trục song song với \(\overrightarrow B \) của từ trường đều. Tốc độ biến thiên thiên \(\frac{{\Delta B}}{{\Delta t}} = 0,2\left( {\frac{T}{s}} \right)\) Lấy \(\pi = 3,14\)
Điện trở của cuộn dây có giá trị bằng bao nhiêu
Sử dụng công thức tính điện trở: \({R_0} = \rho \frac{l}{{{S_0}}}\)
Gọi \(C = \pi d\) là chu vi mỗi vòng dây, chiều dài dợi dây: \(l = C.N = \pi d.N = 3,14.0,1.1000 = 314{\rm{ m}}\)
*Điện trở của sợi dây: \({R_0} = \rho \frac{l}{{{S_0}}} = {2.10^{ - 8}}\frac{{314}}{{0,{{2.10}^{ - 6}}}} = 31,4{\rm{ }}\Omega \).
Đáp án: 31,4
Tính độ lớn suất điện động xuất hiện trong khung (Làm tròn kết quả đến chữ số hàng trăm)
Sử dụng công thức suất điện động cảm ứng: \({e_c} = N\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right|\)
Độ lớn suất điện động: \({e_c} = N\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right| = N.\frac{{\pi {d^2}}}{4}\left| {\frac{{\Delta B}}{{\Delta t}}} \right| = 1000.\frac{{3,14.0,{1^2}}}{4}.0,2 = 1,57{\rm{ }}V\).
Đáp án: 1,57
Hiện nay Uranium tự nhiên chứa hai đồng vị phóng xạ \(^{235}U\) và \(^{238}U,\) với tỉ lệ số hạt \(^{235}U\)và số hạt \(^{238}U\) là \(\frac{7}{{1000}}.\) Biết chu kì bán rã \(^{235}U\) và \(^{238}U\) lần lượt là \(7,{00.10^8}\) năm và \(4,{50.10^9}\) năm. Cách đây bao nhiêu tỉ năm, Uranium tự nhiên có tỷ lệ số hạt \(^{235}U\) và số \(^{238}U\) là \(\frac{3}{{100}}?\)(Kết quả làm tròn đến 2 chử số thập phân sau dấu phẩy)?
Sử dụng công thức số hạt còn lại: \(N = {N_0}{e^{ - \lambda t}}\)
Hiện nay, số hạt \(^{235}U\) và \(^{238}U\) là số hạt còn lại, có tỉ lệ là: \(\frac{{{N_{{0_{235}}}}{2^{\frac{{ - {t_0}}}{{{T_{235}}}}}}}}{{{N_{{0_{238}}}}{2^{\frac{{ - {t_0}}}{{{T_{238}}}}}}}} = \frac{7}{{1000}}\).
Cách đây t năm, tỉ lệ số hạt \(^{235}U\) và \(^{238}U\) là \(\frac{3}{{100}}\) nên ta có: \(\frac{{{N_{{0_{235}}}}{2^{\frac{{ - \left( {{t_0} - t} \right)}}{{{T_{235}}}}}}}}{{{N_{{0_{238}}}}{2^{\frac{{ - \left( {{t_0} - t} \right)}}{{{T_{238}}}}}}}} = \frac{3}{{100}}\)
Lập tỉ số ta được: \(\frac{{\frac{{{N_{{0_{235}}}}{2^{\frac{{ - {t_0}}}{{{T_{235}}}}}}}}{{{N_{{0_{238}}}}{2^{\frac{{ - {t_0}}}{{{T_{238}}}}}}}}}}{{\frac{{{N_{{0_{235}}}}{2^{\frac{{ - \left( {{t_0} - t} \right)}}{{{T_{235}}}}}}}}{{{N_{{0_{238}}}}{2^{\frac{{ - \left( {{t_0} - t} \right)}}{{{T_{238}}}}}}}}}} = \frac{{\frac{7}{{1000}}}}{{\frac{3}{{100}}}} \Leftrightarrow \frac{{{2^{\frac{t}{{{T_{238}}}}}}}}{{{2^{\frac{t}{{{T_{235}}}}}}}} = {2^{t\left( {\frac{1}{{{T_{238}}}} - \frac{1}{{{T_{235}}}}} \right)}} = \frac{7}{{30}}\)
Từ đó \(t = \frac{{\log _2^{\frac{7}{{30}}}}}{{\frac{1}{{{T_{238}}}} - \frac{1}{{{T_{235}}}}}} = \frac{{\log _2^{\frac{7}{{30}}}}}{{\frac{1}{{4,{{5.10}^9}}} - \frac{1}{{{{7.10}^8}}}}} = 1,7404\) tỉ năm.
Đáp án: 1,74
Phát biểu nào sau đây Sai ?
Lực tương tác giữa các phân tử chất rắn ...(1)... nên giữ được các phân tử ở các vị trí cân bằng và mỗi phân tử ... (2). Điền vào chổ trống các cụm từ thích hợp.
Bảng bên dưới cho biết nhiệt độ nóng chảy và nhiệt độ sôi của bốn chất khác nhau. Chất nào tồn tại ở thể lỏng tại
Trong các phát biểu sau đây về sự bay hơi và sự sôi của chất lỏng, phát biểu nào đúng, phát biểu nào sai?
Nội năng của vật phụ thuộc vào
Các bài khác cùng chuyên mục
