-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút - Chương I - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương II - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương III - Giải Tích 12
-
Đề kiểm tra 15 phút – Chương IV – Giải tích 12
-
Đề kiểm tra 15 phút - Chương I - Hình học 12
-
Đề kiểm tra 15 phút - Chương II - Hình học 12
-
Đề kiểm tra 15 phút - Chương III - Hình học 12
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Hình học 12
-
-
Đề thi giữa học kì 1
-
Đề thi học kì 1
-
Đề thi giữa học kì 2
-
Đề thi học kì 2
-
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN
Đề thi giữa kì 1 Toán 12 - Đề số 4
Đề bài
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
-
A.
$f\left( 0 \right) < 5$
-
B.
$f\left( 2 \right) \geqslant 5$
-
C.
$f\left( 1 \right) = 5$
-
D.
$f\left( 0 \right) = 5$
Hàm số \(y = {a^x}\left( {0 < a \ne 1} \right)\) đồng biến khi nào?
-
A.
\(a > 1\)
-
B.
\(0 < a < 1\)
-
C.
\(a \ge 1\)
-
D.
\(a > 0\)
Chọn mệnh đề đúng:
-
A.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
-
B.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 - x} \right)}}{x} = 1\)
-
C.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln x}}{x} = 1\)
-
D.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{{1 + x}} = 1\)
Tập xác định của hàm số $y = - \dfrac{1}{2}{x^3} + 2x - 1$ là:
-
A.
$R$
-
B.
$R\backslash \left\{ 0 \right\}$
-
C.
$\left( { - \infty ;0} \right)$
-
D.
$\left( {0; + \infty } \right)$
Cho lăng trụ xiên tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy $ABC$ một góc \({60^0}\). Thể tích khối lăng trụ là:
-
A.
\(\dfrac{{3{a^3}\sqrt 3 }}{8}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
-
C.
\(\dfrac{{3{a^3}}}{8}\)
-
D.
\(\dfrac{{{a^3}}}{8}\)
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
-
A.
\(2\log a + \log b\)
-
B.
$\log a + 2\log b$
-
C.
$2\left( {\log a + \log b} \right)$
-
D.
$\log a + \dfrac{1}{2}\log b$
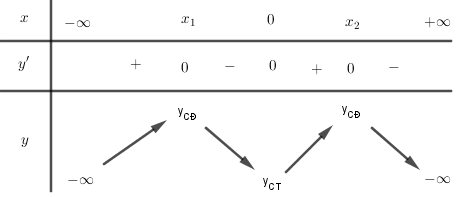
Cho hàm số $y = a{x^4} + b{x^2} + c$ có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
-
A.
$a > 0$
-
B.
$a = 0$
-
C.
$a < 0$
-
D.
$a \ne 0$
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
-
A.
$ab \ge 0$
-
B.
$ab < 0$
-
C.
$b > 0$
-
D.
$b < 0$
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
-
A.
$0 < a < 1$
-
B.
$a > 0$
-
C.
$a > 1$
-
D.
$a < 0$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
-
A.
Giá trị cực tiểu của hàm số là $y = 2$
-
B.
Giá trị cực đại của hàm số là $y = 2$.
-
C.
Giá trị cực tiểu của hàm số là $y = - \infty $
-
D.
Hàm số không có cực trị.
Đẳng thức \(\left( {\sqrt[n]{x}} \right)' = ({x^{\frac{1}{n}}})' = \dfrac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\) xảy ra khi:
-
A.
\(x < 0\)
-
B.
\(x > 0\)
-
C.
\(x \ge 0\)
-
D.
\(x \in R\)
Cho hàm số $y = f\left( x \right)$ nghịch biến và có đạo hàm trên $\left( { - 5;5} \right)$. Khi đó:
-
A.
$f\left( 3 \right) > 0$
-
B.
$f'\left( 0 \right) \le 0$
-
C.
$f'\left( 0 \right) > 0$
-
D.
$f\left( 0 \right) = 0$
Công thức nào sau đây là công thức tăng trưởng mũ?
-
A.
\(T = A.{e^{Nr}}\)
-
B.
\(T = N.{e^{Ar}}\)
-
C.
\(T = r.{e^{NA}}\)
-
D.
\(T = A.{e^{N - r}}\)
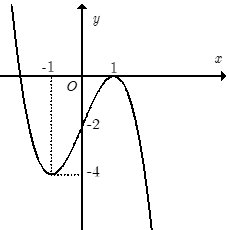
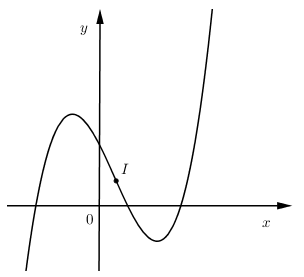
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
-
A.
$a > 0$
-
B.
$a < 0$
-
C.
$a = 0$
-
D.
$a \leqslant 0$
Cho $m,n \in Z$, khi đó:
-
A.
${a^{m.n}} = {a^m}.{a^n}$
-
B.
${a^{mn}} = {a^m} + {a^n}$
-
C.
${a^{mn}} = {a^m}:{a^n}$
-
D.
${a^{mn}} = {\left( {{a^m}} \right)^n}$
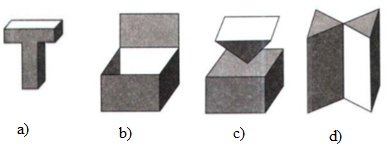
Trong các hình dưới đây, hình nào là khối đa diện?
-
A.
Hình a
-
B.
Hình c
-
C.
Hình d
-
D.
Hình b
Viết các số sau theo thứ tự tăng dần: $a = {1^{3,8}};\,\,b = {2^{ - 1}};\,\,c = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$
-
A.
$b;\,c;\,a$
-
B.
$c;\,a;\,b$
-
C.
$c;b;a$
-
D.
$b;\,a;\,c$
Chọn mệnh đề đúng:
-
A.
Nếu hai hình \(H\) và \(H'\) bằng nhau thì có một phép tịnh tiến biến hình này thành hình kia.
-
B.
Nếu có một phép tịnh tiến biến hình \(H'\) thành \(H\) thì chúng bằng nhau.
-
C.
Nếu hai hình \(H\) và \(H'\) bằng nhau thì có một phép đồng nhất biến hình này thành hình kia.
-
D.
Nếu hai hình \(H\) và \(H'\) bằng nhau thì chúng trùng nhau.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là:
-
A.
$\left( {1;\, - 2} \right)$
-
B.
$\left( { - 1;\,2} \right)$
-
C.
$\left( {1;\,2} \right)$
-
D.
$\left( { - 1;\,1} \right)$
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{2x + c}}\) có tiệm cận ngang \(y = 2\) và tiệm cận đứng \(x = 1\) thì \(a + c\) bằng
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(6\)
Cho hình chóp đều $S.ABCD$ có cạnh bên và cạnh đáy bằng $a$. Thể tích của khối chóp $S.ABCD$ là:
-
A.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
-
B.
\(\dfrac{{{a^2}\sqrt 2 }}{2}\)
-
C.
\(\dfrac{{{a^3}}}{2}\)
-
D.
\({a^3}\)
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
-
A.
\(x \in R\)
-
B.
\(x \ne 3\)
-
C.
\(x \ne 2\)
-
D.
\(x \ne - 2\)
Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:
-
A.
$\left( {1;3} \right)$
-
B.
$\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$
-
C.
$\left( {1;3} \right)$ và $\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$
-
D.
$\left( { - 1; - 3} \right)$
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
-
A.
bằng nhau
-
B.
trùng nhau
-
C.
có các đỉnh trùng nhau
-
D.
có đáy trùng nhau
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
-
A.
$m = 1$
-
B.
$m = 2$
-
C.
$m = 3$
-
D.
$m = 4$
Logarit cơ số $a$ của $b$ kí hiệu là:
-
A.
${\log _a}b$
-
B.
${\log _b}a$
-
C.
${\ln _a}b$
-
D.
${\ln _b}a$
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?
-
A.
\(y = \dfrac{1}{{2x}}\)
-
B.
\(y=\dfrac{{2x - 1}}{{x + 1}}\)
-
C.
\(y = \sqrt {{x^2} + 1} \)
-
D.
\(y = \dfrac{{x - 1}}{{{x^2} - 1}}\)
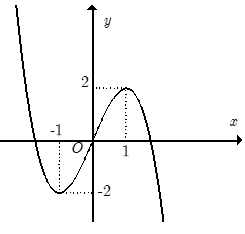
Hàm số nào sau đây có đồ thị như hình vẽ?
-
A.
$y = - {x^4} - 2{x^2} + 3$
-
B.
$y = {x^4} - 2{x^2} - 3$
-
C.
$y = - {x^4} - 2{x^2} - 3$
-
D.
$y = {x^4} + 2{x^2} - 3$
Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là:
-
A.
Giá trị cực đại của hàm số.
-
B.
Giá trị cực đại của đồ thị hàm số.
-
C.
Điểm cực đại của hàm số.
-
D.
Điểm cực đại của đồ thị hàm số.
Chọn kết luận đúng:
-
A.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\) với mọi \(\alpha \in R\).
-
B.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\) với mọi \(\alpha \in Z\).
-
C.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\backslash \left\{ 0 \right\}\) với mọi \(\alpha \in Z\).
-
D.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = \left( {0; + \infty } \right)\) với mọi \(\alpha \) không nguyên.
Thể tích khối hộp chữ nhật có diện tích đáy \(S\) và độ dài cạnh bên \(a\) là:
-
A.
\(V = S.a\)
-
B.
\(V = {S^2}a\)
-
C.
\(V = \dfrac{1}{3}Sa\)
-
D.
\(V = \dfrac{{{S^2}}}{a}\)
Vật thể nào trong các vật thể sau không phải là khối đa diện?
-
A.
Hình 1
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 4
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
-
A.
$m < - \dfrac{1}{3}$
-
B.
$m \leqslant - \dfrac{1}{3}$
-
C.
$m \leqslant - \dfrac{4}{3}$
-
D.
$m \leqslant 0$
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Số điểm cực trị của hàm số \(f\left( {{x^2} - 2x} \right)\) là:
-
A.
\(4\)
-
B.
\(2\)
-
C.
\(5\)
-
D.
\(3\)
Cho hàm số $y = \dfrac{1}{3}{x^3} - m{x^2} + (2m - 4)x - 3.$ Tìm $m$ để hàm số có các điểm cực đại, cực tiểu ${x_1};{x_2}$ thỏa mãn: $x_1^2 + x_2^2 = {x_1}.{x_2} + 10$
-
A.
$m = 1$
-
B.
$m = \dfrac{1}{2}$
-
C.
$m = 1;m = \dfrac{1}{2}$
-
D.
$m = 3$
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Xét hàm số \(g\left( x \right) = f\left( {{x^3} + 2x} \right) + m\). Giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) bằng \(9\) là:
-
A.
\(m = 10\)
-
B.
\(m = 6\)
-
C.
\(m = 12\)
-
D.
\(m = 8\)
Cho hàm số \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\,\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
Trong các số \(a,\,\,b\) và \(c\) có bao nhiêu số dương ?
-
A.
\(2.\)
-
B.
\(3.\)
-
C.
\(1.\)
-
D.
\(0.\)
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên sau:
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số \(y = f\left( x \right)\)?
-
A.
-
B.
-
C.
-
D.
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
Chọn khẳng định đúng:
-
A.
$b + c + d = 1$
-
B.
$b + c + d = 3$
-
C.
$b + c + d = 5$
-
D.
$b + c + d = 10$
Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$
-
A.
$m = \dfrac{1}{4}$
-
B.
$m > - \dfrac{1}{2}$
-
C.
$m > - \dfrac{1}{4}$
-
D.
$m \geqslant - \dfrac{1}{4}$
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).
-
A.
\(6\)
-
B.
\(5\)
-
C.
\(8\)
-
D.
\(7\)
Cho các số dương $a, b, c, d$. Biểu thức $S = \ln \dfrac{a}{b}+ \ln \dfrac{b}{c} + \ln \dfrac{c}{d}+\ln \dfrac{d}{a}$ bằng:
-
A.
$0$
-
B.
$1$
-
C.
$\ln (\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{d}+\dfrac{d}{a})$
-
D.
$\ln (abcd)$
Cho giới hạn \(I = \mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{3x}} - {e^{2x}}}}{x}\), chọn mệnh đề đúng:
-
A.
\({I^2} + 3I = 2\)
-
B.
\({I^3} + {I^2} - 2 = 0\)
-
C.
\(\dfrac{{I - 1}}{{I + 1}} = 1\)
-
D.
\(3I - 2 = 2{I^2}\)
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?
-
A.
\(12.\)
-
B.
\(10.\)
-
C.
\(4.\)
-
D.
\(8.\)
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
-
A.
\(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
-
C.
\(\dfrac{{{a^3}\sqrt 3 }}{6}\)
-
D.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
Bà Hoa gửi $100$ triệu vào tài khoản định kì tính lãi suất là $8\% $ một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
-
A.
$81,412$ triệu
-
B.
$115,892$ triệu
-
C.
$119$ triệu
-
D.
$78$ triệu
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
-
A.
\(\dfrac{{{a^3}\sqrt 3 }}{3}\)
-
B.
\(4{a^3}\sqrt 3 \)
-
C.
\({a^3}\sqrt 3 \)
-
D.
\(\dfrac{{4{a^3}\sqrt 3 }}{3}\)
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có \(6\) nghiệm phân biệt
-
A.
\(2\).
-
B.
\(4\).
-
C.
\(3\).
-
D.
\(5\).
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
-
A.
\(m < f\left( 0 \right)\)
-
B.
\(m < f\left( 1 \right) - 1\)
-
C.
\(m < f\left( { - 1} \right) + 1\)
-
D.
\(m < f\left( 2 \right)\)
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A.\) Cạnh \(BC = 2a\) và \(\angle ABC = {60^0}.\) Biết tứ giác \(BCC'B'\) là hình thoi có \(\angle B'BC\) nhọn. Mặt phẳng \(\left( {BCC'B'} \right)\) vuông góc với \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ABB'A'} \right)\) tạo với \(\left( {ABC} \right)\) góc \({45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
-
A.
\(\dfrac{{\sqrt 7 {a^3}}}{7}\)
-
B.
\(\dfrac{{3\sqrt 7 {a^3}}}{7}\)
-
C.
\(\dfrac{{6\sqrt 7 {a^3}}}{7}\)
-
D.
\(\dfrac{{\sqrt 7 {a^3}}}{{21}}\)
Lời giải và đáp án
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
-
A.
$f\left( 0 \right) < 5$
-
B.
$f\left( 2 \right) \geqslant 5$
-
C.
$f\left( 1 \right) = 5$
-
D.
$f\left( 0 \right) = 5$
Đáp án : B
GTNN của $f\left( x \right)$ trên $\left[ {0;2} \right]$ bằng $5$ nên $f\left( x \right) \geqslant 5,\forall x \in \left[ {0;2} \right] \Rightarrow f\left( 2 \right) \geqslant 5$.
Hàm số \(y = {a^x}\left( {0 < a \ne 1} \right)\) đồng biến khi nào?
-
A.
\(a > 1\)
-
B.
\(0 < a < 1\)
-
C.
\(a \ge 1\)
-
D.
\(a > 0\)
Đáp án : A
Hàm số mũ \(y = {a^x}\left( {0 < a \ne 1} \right)\) đồng biến khi \(a > 1\).
Chọn mệnh đề đúng:
-
A.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
-
B.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 - x} \right)}}{x} = 1\)
-
C.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln x}}{x} = 1\)
-
D.
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{{1 + x}} = 1\)
Đáp án : A
Giới hạn cần nhớ: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
Tập xác định của hàm số $y = - \dfrac{1}{2}{x^3} + 2x - 1$ là:
-
A.
$R$
-
B.
$R\backslash \left\{ 0 \right\}$
-
C.
$\left( { - \infty ;0} \right)$
-
D.
$\left( {0; + \infty } \right)$
Đáp án : A
Hàm đa thức bậc ba xác định trên $R$.
Cho lăng trụ xiên tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy $ABC$ một góc \({60^0}\). Thể tích khối lăng trụ là:
-
A.
\(\dfrac{{3{a^3}\sqrt 3 }}{8}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
-
C.
\(\dfrac{{3{a^3}}}{8}\)
-
D.
\(\dfrac{{{a^3}}}{8}\)
Đáp án : A
- Tính diện tích đáy \({S_{\Delta ABC}}\)
- Xác định góc \({60^0}\): góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính độ dài đường cao của lăng trụ.
- Tính thể tích lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
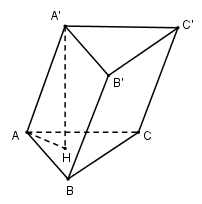
Gọi $H$ là hình chiếu vuông góc của $A'$ trên \(\left( {ABC} \right) \Rightarrow A'H \bot \left( {ABC} \right)\)
\( \Rightarrow AH\) là hình chiếu vuông góc của $AA'$ trên \(\left( {ABC} \right) \Rightarrow \widehat {\left( {AA';\left( {ABC} \right)} \right)} = \widehat {\left( {AA';AH} \right)} = \widehat {A'AH} = {60^0}\)
\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AH \Rightarrow \Delta A'AH\) vuông tại \(H \Rightarrow A'H = AA'.\sin 60 = a\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{2}\)
Tam giác $ABC$ đều cạnh nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}\sqrt 3 }}{8}\)
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
-
A.
\(2\log a + \log b\)
-
B.
$\log a + 2\log b$
-
C.
$2\left( {\log a + \log b} \right)$
-
D.
$\log a + \dfrac{1}{2}\log b$
Đáp án : B
Sử dụng các công thức biến đổi logarit: \(\log \left( {xy} \right) = \log x + \log y;\;\;\log {x^n} = n\log x\) với \(x;y\) là các số thực dương.
Ta có: \(\log \left( {a{b^2}} \right) = \log a + \log {b^2} = \log a + 2\log b\)
Cho hàm số $y = a{x^4} + b{x^2} + c$ có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
-
A.
$a > 0$
-
B.
$a = 0$
-
C.
$a < 0$
-
D.
$a \ne 0$
Đáp án : C
Từ bảng biến thiên ta thấy $\mathop {\lim }\limits_{x \to \pm \infty } y = - \infty $ nên $a < 0$.
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
-
A.
$ab \ge 0$
-
B.
$ab < 0$
-
C.
$b > 0$
-
D.
$b < 0$
Đáp án : A
Ta có: $y' = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right)$.
Hàm số có $1$ cực trị $ \Leftrightarrow y' = 0$ có $1$ nghiệm duy nhất hay $y'=0$ vô nghiệm hoặc có nghiệm kép
\( \Leftrightarrow \left[ \begin{array}{l}ab > 0\\b \ge 0\end{array} \right. \Leftrightarrow ab \ge 0\)
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
-
A.
$0 < a < 1$
-
B.
$a > 0$
-
C.
$a > 1$
-
D.
$a < 0$
Đáp án : C
Sử dụng so sánh lũy thừa:
+ Với \(a > 1\) thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+ Với \(0 < a < 1\) thì \({a^m} > {a^n} \Leftrightarrow m < n\)
\({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2} \Leftrightarrow {a^{0,2}} < {a^2}\)
Do \(0,2 < 2\) và có số mũ không nguyên nên ${a^{0,2}} < {a^2}$ khi $a > 1$.
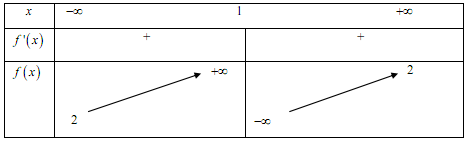
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
-
A.
Giá trị cực tiểu của hàm số là $y = 2$
-
B.
Giá trị cực đại của hàm số là $y = 2$.
-
C.
Giá trị cực tiểu của hàm số là $y = - \infty $
-
D.
Hàm số không có cực trị.
Đáp án : D
Quan sát bảng biến thiên và nhận xét dấu của đạo hàm.
Từ bảng biến thiên ta thấy, đạo hàm không đổi dấu trên $\left( { - \infty ; + \infty } \right)$ nên hàm số không có cực trị.
Đẳng thức \(\left( {\sqrt[n]{x}} \right)' = ({x^{\frac{1}{n}}})' = \dfrac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\) xảy ra khi:
-
A.
\(x < 0\)
-
B.
\(x > 0\)
-
C.
\(x \ge 0\)
-
D.
\(x \in R\)
Đáp án : B
Sử dụng điều kiện để đẳng thức \(\sqrt[n]{x} = {x^{\frac{1}{n}}}\) xảy ra là \(x > 0\).
Vì \(\sqrt[n]{x} = {x^{\frac{1}{n}}}\) nếu \(x > 0\) nên \(\left( {\sqrt[n]{x}} \right)' = ({x^{\frac{1}{n}}})' = \dfrac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\) chỉ đúng nếu \(x > 0\).
Cho hàm số $y = f\left( x \right)$ nghịch biến và có đạo hàm trên $\left( { - 5;5} \right)$. Khi đó:
-
A.
$f\left( 3 \right) > 0$
-
B.
$f'\left( 0 \right) \le 0$
-
C.
$f'\left( 0 \right) > 0$
-
D.
$f\left( 0 \right) = 0$
Đáp án : B
Sử dụng tính chất: Hàm số $f\left( x \right)$ nghịch biến trên $\left( {a;b} \right)$ thì $f'\left( x \right) \le 0,\forall x \in \left( {a;b} \right)$.
Vì $y = f\left( x \right)$ nghịch biến trên $\left( { - 5;5} \right)$ nên $f'\left( x \right) \le 0,\forall x \in \left( { - 5;5} \right)$.
Vậy $f'\left( 0 \right) \le 0$.
Công thức nào sau đây là công thức tăng trưởng mũ?
-
A.
\(T = A.{e^{Nr}}\)
-
B.
\(T = N.{e^{Ar}}\)
-
C.
\(T = r.{e^{NA}}\)
-
D.
\(T = A.{e^{N - r}}\)
Đáp án : A
Công thức lãi kép (hoặc công thức tăng trưởng mũ):
\(T = A.{e^{Nr}}\), ở đó \(A\) là số tiền gửi ban đầu, \(r\) là lãi suất, \(N\) là số kì hạn.
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
-
A.
$a > 0$
-
B.
$a < 0$
-
C.
$a = 0$
-
D.
$a \leqslant 0$
Đáp án : A
Quan sát đồ thị ta thấy $\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty $ nên $a > 0$.
Cho $m,n \in Z$, khi đó:
-
A.
${a^{m.n}} = {a^m}.{a^n}$
-
B.
${a^{mn}} = {a^m} + {a^n}$
-
C.
${a^{mn}} = {a^m}:{a^n}$
-
D.
${a^{mn}} = {\left( {{a^m}} \right)^n}$
Đáp án : D
Với $m,n \in Z$ thì ${a^{mn}} = {\left( {{a^m}} \right)^n}$.
Trong các hình dưới đây, hình nào là khối đa diện?
-
A.
Hình a
-
B.
Hình c
-
C.
Hình d
-
D.
Hình b
Đáp án : A
Sử dụng tính chất khối đa diện: mối cạnh là cạnh chung của đúng hai mặt.
Trong các hình đã cho chỉ có hình a) là khối đa diện.
Hình b) có 3 cạnh ở trên không phải cạnh chung của 2 mặt, hình c) và d) có 1 cạnh là không là cạnh chung của 2 mặt.
Viết các số sau theo thứ tự tăng dần: $a = {1^{3,8}};\,\,b = {2^{ - 1}};\,\,c = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$
-
A.
$b;\,c;\,a$
-
B.
$c;\,a;\,b$
-
C.
$c;b;a$
-
D.
$b;\,a;\,c$
Đáp án : D
Tính giá trị các số $a,b,c$ và so sánh.
Ta có: $a = {1^{3,8}} = 1$; $b = {2^{ - 1}} = \dfrac{1}{2} = 0,5$ và $c = {\left( {\dfrac{1}{2}} \right)^{ - 3}} = {2^3} = 8.$
Mà $0,5 < 1 < 8 \Rightarrow b < a < c$
Chọn mệnh đề đúng:
-
A.
Nếu hai hình \(H\) và \(H'\) bằng nhau thì có một phép tịnh tiến biến hình này thành hình kia.
-
B.
Nếu có một phép tịnh tiến biến hình \(H'\) thành \(H\) thì chúng bằng nhau.
-
C.
Nếu hai hình \(H\) và \(H'\) bằng nhau thì có một phép đồng nhất biến hình này thành hình kia.
-
D.
Nếu hai hình \(H\) và \(H'\) bằng nhau thì chúng trùng nhau.
Đáp án : B
- Nếu có một phép dời hình biến hình \(H'\) thành \(H\) thì hai hình bằng nhau và phép tịnh tiến cũng là một phép dời hình nên B đúng.
- Các đáp án A, C, D đều sai vì hai hình bằng nhau có thể là hợp thành của một số phép dời hình chứ không nhất thiết là chỉ một phép dời hình.
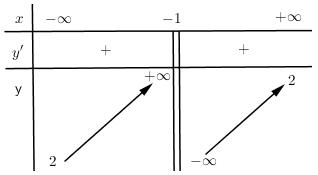
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là:
-
A.
$\left( {1;\, - 2} \right)$
-
B.
$\left( { - 1;\,2} \right)$
-
C.
$\left( {1;\,2} \right)$
-
D.
$\left( { - 1;\,1} \right)$
Đáp án : B
Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số rồi tìm giao điểm của chúng.
Từ bảng biến thiên ta có:
- Tiệm cận đứng của đồ thị hàm số là $x = - 1.$
- Tiệm cận ngang của đồ thị hàm số là $y = 2.$
Vậy tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là $\left( { - 1;2} \right)$
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{2x + c}}\) có tiệm cận ngang \(y = 2\) và tiệm cận đứng \(x = 1\) thì \(a + c\) bằng
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(6\)
Đáp án : B
Xác định được hai đường tiệm cận của đồ thị hàm số bậc nhất trên bậc nhất
Ta có \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } {\mkern 1mu} \dfrac{{ax + b}}{{2x + c}} = \dfrac{a}{2} \Rightarrow y = \dfrac{a}{2}\) là tiệm cận ngang của ĐTHS
\( \Rightarrow \dfrac{a}{2} = 2 \Rightarrow a = 4.\)
Và \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - {\kern 1pt} \dfrac{c}{2}} {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - {\kern 1pt} \dfrac{c}{2}} {\mkern 1mu} \dfrac{{ax + b}}{{2x + c}} = \infty \Rightarrow x = - \dfrac{c}{2}\) là tiệm cận đứng của ĐTHS
\( \Rightarrow - \dfrac{c}{2} = 1 \Rightarrow c = - {\mkern 1mu} 2.\)
Vậy tổng \(a + c = 4 - 2 = 2.\)
Cho hình chóp đều $S.ABCD$ có cạnh bên và cạnh đáy bằng $a$. Thể tích của khối chóp $S.ABCD$ là:
-
A.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
-
B.
\(\dfrac{{{a^2}\sqrt 2 }}{2}\)
-
C.
\(\dfrac{{{a^3}}}{2}\)
-
D.
\({a^3}\)
Đáp án : A
- Bước 1: Tính diện tích đáy \({S_{ABCD}}\)
- Bước 2: Tính chiều cao \(h = SO\).
- Bước 3: Tính thể tích \(V = \dfrac{1}{3}Sh\).
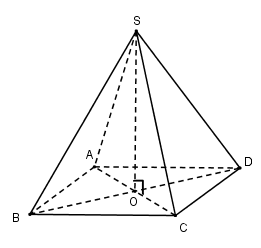
Gọi \(O = AC \cap BD\)
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Ta có: \(AC = BD = a\sqrt 2 \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O \( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
-
A.
\(x \in R\)
-
B.
\(x \ne 3\)
-
C.
\(x \ne 2\)
-
D.
\(x \ne - 2\)
Đáp án : C
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) xác định khi \(x \ne - \dfrac{d}{c}\).
Hàm số xác định khi \(x - 2 \ne 0 \Leftrightarrow x \ne 2\).
Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:
-
A.
$\left( {1;3} \right)$
-
B.
$\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$
-
C.
$\left( {1;3} \right)$ và $\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$
-
D.
$\left( { - 1; - 3} \right)$
Đáp án : C
- Bước 1: Lập phương trình hoành độ giao điểm của đồ thị hàm số.
- Bước 2: Giải phương trình tìm $x$, rồi từ đó suy ra $y$ và tọa độ giao điểm.
Phương trình hoành độ $2{x^2} + 1 = 3x$.
$ \Leftrightarrow 2{x^2} - 3x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \Rightarrow y = 3 \hfill \\ x = \dfrac{1}{2} \Rightarrow y = \dfrac{3}{2} \hfill \\ \end{gathered} \right.$
Vậy có hai giao điểm là $\left( {1;3} \right)$ và $\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$.
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
-
A.
bằng nhau
-
B.
trùng nhau
-
C.
có các đỉnh trùng nhau
-
D.
có đáy trùng nhau
Đáp án : A
Hai tứ diện bằng nhau nếu chúng có các cạnh tương ứng bằng nhau.
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
-
A.
$m = 1$
-
B.
$m = 2$
-
C.
$m = 3$
-
D.
$m = 4$
Đáp án : C
- Bước 1: Tính $y',y''$.
- Bước 2: Nêu điều kiện để $x = {x_0}$ là cực trị của hàm số:
+ $x = {x_0}$ là điểm cực đại nếu $\left\{ \begin{gathered} f'\left( {{x_0}} \right) = 0 \hfill \\f''\left( {{x_0}} \right) < 0 \hfill \\ \end{gathered} \right.$
+ $x = {x_0}$ là điểm cực tiểu nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered} \right.$
- Bước 3: Kết luận.
TXĐ $D = \mathbb{R}$
$y' = - {x^2} + \dfrac{2}{3}mx \Rightarrow y'' = - 2x + \dfrac{2}{3}m$
Hàm số đã cho đạt cực đại tại $x = 2$
$ \Leftrightarrow \left\{ \begin{gathered} y'(2) = 0 \hfill \\ y''\left( 2 \right) < 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} - {2^2} + \dfrac{2}{3}m.2 = 0 \hfill \\ - 2.2 + \dfrac{2}{3}m. < 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} - 4 + \dfrac{4}{3}m = 0 \hfill \\- 4 + \dfrac{2}{3}m < 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} m = 3 \hfill \\m < 6 \hfill \\ \end{gathered} \right. \Leftrightarrow m = 3$
Logarit cơ số $a$ của $b$ kí hiệu là:
-
A.
${\log _a}b$
-
B.
${\log _b}a$
-
C.
${\ln _a}b$
-
D.
${\ln _b}a$
Đáp án : A
Số ${\log _a}b$ được gọi là lôgarit cơ số $a$ của $b$.
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?
-
A.
\(y = \dfrac{1}{{2x}}\)
-
B.
\(y=\dfrac{{2x - 1}}{{x + 1}}\)
-
C.
\(y = \sqrt {{x^2} + 1} \)
-
D.
\(y = \dfrac{{x - 1}}{{{x^2} - 1}}\)
Đáp án : C
Tìm txđ của mỗi hàm số rồi kết luận.
Đáp án A: Hàm số xác định nếu \(x \ne 0\) nên loại.
Đáp án B: Hàm số xác định nếu \(x \ne - 1\) nên loại.
Đáp án C: Hàm số xác định nếu \({x^2} + 1 \ge 0\) luôn đúng nên C đúng.
Đáp án D: Hàm số xác định nếu \({x^2} - 1 \ne 0 \Leftrightarrow x \ne \pm 1\) nên loại.
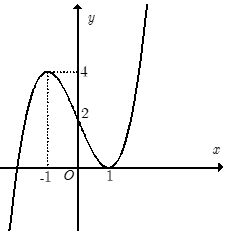
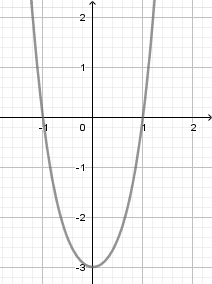
Hàm số nào sau đây có đồ thị như hình vẽ?
-
A.
$y = - {x^4} - 2{x^2} + 3$
-
B.
$y = {x^4} - 2{x^2} - 3$
-
C.
$y = - {x^4} - 2{x^2} - 3$
-
D.
$y = {x^4} + 2{x^2} - 3$
Đáp án : D
Quan sát đồ thị hàm số và nhận xét dáng điệu đồ thị, điểm cực đại, cực tiểu, đối chiếu các đáp án đã cho.
Từ dáng đồ thị ta có $a > 0$ nên loại A, C
Đồ thị hàm số có điểm cực tiểu là $\left( {0; - 3} \right).$
Do hàm số chỉ có một điểm cực trị nên $y' = 0$ phải có duy nhất một nghiệm ${x_0}$ và $y\left( {{x_0}} \right) = - 3.$
Kiểm tra ta chỉ thấy đáp án D là phù hợp.
Ngoài ra, đáp án B bị loại vì phương trình $y'=0$ ở đáp án B có $3$ nghiệm phân biệt.
Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là:
-
A.
Giá trị cực đại của hàm số.
-
B.
Giá trị cực đại của đồ thị hàm số.
-
C.
Điểm cực đại của hàm số.
-
D.
Điểm cực đại của đồ thị hàm số.
Đáp án : D
Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là điểm cực đại của đồ thị hàm số.
Chọn kết luận đúng:
-
A.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\) với mọi \(\alpha \in R\).
-
B.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\) với mọi \(\alpha \in Z\).
-
C.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\backslash \left\{ 0 \right\}\) với mọi \(\alpha \in Z\).
-
D.
Hàm số \(y = {x^\alpha }\) có TXĐ \(D = \left( {0; + \infty } \right)\) với mọi \(\alpha \) không nguyên.
Đáp án : D
- Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\) với mọi \(\alpha \) nguyên dương nên A và B sai.
- Hàm số \(y = {x^\alpha }\) có TXĐ \(D = R\backslash \left\{ 0 \right\}\) với mọi \(\alpha \) nguyên âm hoặc \(\alpha = 0\) nên C sai.
- Hàm số \(y = {x^\alpha }\) có TXĐ \(D = \left( {0; + \infty } \right)\) với mọi \(\alpha \) không nguyên nên D đúng.
Thể tích khối hộp chữ nhật có diện tích đáy \(S\) và độ dài cạnh bên \(a\) là:
-
A.
\(V = S.a\)
-
B.
\(V = {S^2}a\)
-
C.
\(V = \dfrac{1}{3}Sa\)
-
D.
\(V = \dfrac{{{S^2}}}{a}\)
Đáp án : A
Sử dụng công thức tính thể tích khối lăng trụ \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Hình hộp chữ nhật có cạnh bên vuông góc với đáy nên cạnh bên chính là đường cao.
Vì hình hộp chữ nhật cũng là hình lăng trụ nên thể tích của khối hộp cũng được tính bởi công thức \(V = Sh\), hay \(V = Sa\).
Vật thể nào trong các vật thể sau không phải là khối đa diện?
-
A.
Hình 1
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 4
Đáp án : C
Khái niệm khối đa diện: Khối đa diện là hình được tạo bởi hữu hạn các đa giác thỏa mãn hai điều kiện:
+ Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
+ Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Quan sát bốn hình, có hình C có cạnh là cạnh chung của 4 đa giác, vậy hình này không phải khối đa diện.
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
-
A.
$m < - \dfrac{1}{3}$
-
B.
$m \leqslant - \dfrac{1}{3}$
-
C.
$m \leqslant - \dfrac{4}{3}$
-
D.
$m \leqslant 0$
Đáp án : B
- Bước 1: Nêu điều kiện để hàm số đơn điệu trên $D$:
+ Hàm số $y = f\left( x \right)$ đồng biến trên $D \Leftrightarrow y' = f'\left( x \right) \geqslant 0,\forall x \in D$.
+ Hàm số $y = f\left( x \right)$ nghịch biến trên $D \Leftrightarrow y' = f'\left( x \right) \leqslant 0,\forall x \in D$.
- Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm $m$.
Chú ý: Dưới đây là một trong những cách hay được sử dụng:
- Rút $m$ theo $x$ sẽ xảy ra một trong hai trường hợp: $m \geqslant g\left( x \right),\forall x \in D$ hoặc $m \leqslant g\left( x \right),\forall x \in D$.
- Khảo sát tính đơn điệu của hàm số $y = g\left( x \right)$ trên $D$.
- Kết luận: Đánh giá $g(x)$ suy ra giá trị của $m$
- Bước 3: Kết luận.
Ta có: $y' = {x^2} - 4mx + 4m$.
Hàm số nghịch biến trên $\left( { - 2;0} \right) \Rightarrow y' \leqslant 0,\forall x \in \left( { - 2;0} \right) \Leftrightarrow {x^2} - 4mx + 4m \leqslant 0,\forall x \in \left( { - 2;0} \right)$ $ \Leftrightarrow {x^2} - 4m\left( {x - 1} \right) \leqslant 0 \Leftrightarrow 4m\left( {x - 1} \right) \geqslant {x^2} \Leftrightarrow 4m \leqslant \dfrac{{{x^2}}}{{x- 1}}$ (vì $ - 2 < x < 0$)
Xét hàm $g\left( x \right) = \dfrac{{{x^2}}}{{x - 1}}$ trên $\left( { - 2;0} \right)$ ta có:
$g'\left( x \right) = \dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \notin \left( { - 2;0} \right) \hfill \\x = 2 \notin \left( { - 2;0} \right) \hfill \\ \end{gathered} \right. \Rightarrow g'\left( x \right) > 0,\forall x \in \left( { - 2;0} \right)$
Do đó hàm số $y = g\left( x \right)$ đồng biến trên $\left( { - 2;0} \right)$
Suy ra \(g\left( { - 2} \right) < g\left( x \right) < g\left( 0 \right),\forall x \in \left( { - 2;0} \right)\) hay \( - \dfrac{4}{3} < g\left( x \right) < 0,\forall x \in \left( { - 2;0} \right)\)
Khi đó \(4m \le g\left( x \right),\forall x \in \left( { - 2;0} \right) \Leftrightarrow 4m \le - \dfrac{4}{3} \Leftrightarrow m \le - \dfrac{1}{3}\)
Vậy $m \leqslant - \dfrac{1}{3}$
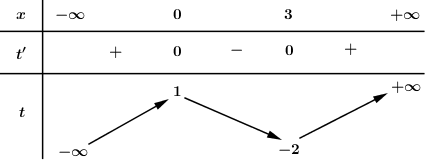
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Số điểm cực trị của hàm số \(f\left( {{x^2} - 2x} \right)\) là:
-
A.
\(4\)
-
B.
\(2\)
-
C.
\(5\)
-
D.
\(3\)
Đáp án : C
Số điểm cực trị của hàm số \(y = f\left( x \right)\) là số nghiệm bội lẻ của phương trình \(g'\left( x \right) = 0\).
Đặt \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) ta có \(g'\left( x \right) = \left( {2x - 2} \right)f'\left( {{x^2} - 2x} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\f'\left( {{x^2} - 2x} \right) = 0\end{array} \right.\).
Dựa vào BBT ta thấy \(f'\left( {{x^2} - 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2x = 0\\{x^2} - 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = -1\\x = 3\end{array} \right.\)
\( \Rightarrow \) Phương trình \(g'\left( x \right) = 0\) có 5 nghiệm đơn \(x = 0,\,\,x = 2,\,\,x = 3,x=-1,x=1\)
Vậy hàm số đã cho có 5 điểm cực trị.
Cho hàm số $y = \dfrac{1}{3}{x^3} - m{x^2} + (2m - 4)x - 3.$ Tìm $m$ để hàm số có các điểm cực đại, cực tiểu ${x_1};{x_2}$ thỏa mãn: $x_1^2 + x_2^2 = {x_1}.{x_2} + 10$
-
A.
$m = 1$
-
B.
$m = \dfrac{1}{2}$
-
C.
$m = 1;m = \dfrac{1}{2}$
-
D.
$m = 3$
Đáp án : C
- Bước 1: Tính $y'$.
- Bước 2: Tìm điều kiện để hàm số có hai cực trị $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt.
- Bước 3: Sử dụng hệ thức Vi-et để thay $\left\{ \begin{gathered} {x_1} + {x_2} = S \hfill \\{x_1}{x_2} = P \hfill \\\end{gathered} \right.$ và tìm $m$.
\(y' = {x^2} - 2mx + 2m - 4\)
Để hàm số có cực đại cực tiểu \( \Leftrightarrow \Delta ' > 0,\forall m \Leftrightarrow {m^2} - 2m + 4 > 0,\forall m\)
Khi đó phương trình $y'=0$ có hai nghiệm $x_1,x_2$ thỏa mãn
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a} = 2m\\{x_1}{x_2} = \dfrac{c}{a} = 2m - 4\end{array} \right.\)
Ta có:
\(\begin{array}{l}x_1^2 + x_2^2 = {x_1}.{x_2} + 10\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} - {x_1}{x_2} - 10 = 0\\ \Leftrightarrow {({x_1} + {x_2})^2} - 3{x_1}{x_2} - 10 = 0\\ \Leftrightarrow {(2m)^2} - 3.(2m - 4) - 10 = 0\\ \Leftrightarrow 4{m^2} - 6m + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \dfrac{1}{2}\end{array} \right.\end{array}\)
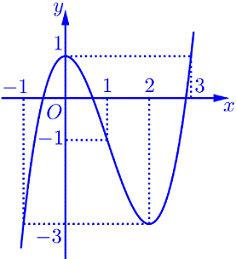
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Xét hàm số \(g\left( x \right) = f\left( {{x^3} + 2x} \right) + m\). Giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) bằng \(9\) là:
-
A.
\(m = 10\)
-
B.
\(m = 6\)
-
C.
\(m = 12\)
-
D.
\(m = 8\)
Đáp án : D
- Tính đạo hàm của hàm số \(y = g\left( x \right)\). Giải phương trình \(g'\left( x \right) = 0\).
- Tìm giá trị lớn nhất của hàm số trên đoạn \(\left[ {0;1} \right]\) để tìm giá trị của \(m\).
Ta có : \(g'\left( x \right) = \left( {3{x^2} + 2} \right).f'\left( {{x^3} + 2x} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 2 = 0\\f'\left( {{x^3} + 2x} \right) = 0\end{array} \right. \Leftrightarrow f'\left( {{x^3} + 2x} \right) = 0\) (Do phương trình \(3{x^2} + 2 = 0\) vô nghiệm).
Từ đồ thị hàm số \(f\left( x \right)\) đã cho ta có : \(f'\left( {{x^3} + 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^3} + 2x = 0\\{x^3} + 2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = {x_0} \approx 0,77\end{array} \right.\)
Hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) có :
\(\begin{array}{l}g\left( 0 \right) = f\left( 0 \right) + m = m + 1\\g\left( {{x_0}} \right) = f\left( 2 \right) + m = m - 3\\g\left( 1 \right) = f\left( 3 \right) + m = m + 1\end{array}\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right) = g\left( 1 \right) = m + 1\).
Theo giả thiết, giá trị lớn nhất của hàm số \(g\left( x \right)\) trên \(\left[ {0;1} \right]\) bằng 9 nên \(m + 1 = 9 \Leftrightarrow m = 8\).
Vậy \(m = 8.\)
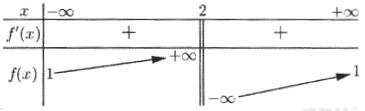
Cho hàm số \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\,\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
Trong các số \(a,\,\,b\) và \(c\) có bao nhiêu số dương ?
-
A.
\(2.\)
-
B.
\(3.\)
-
C.
\(1.\)
-
D.
\(0.\)
Đáp án : C
Từ BBT suy ra các đường TCĐ, TCN của đồ thị hàm số.
Từ đó suy ra mối quan hệ của \(a,\,\,b,\,\,c.\)
Dựa vào BBT ta thấy đồ thị hàm số có TCĐ: \(x = 2\) \( \Rightarrow - \dfrac{c}{b} = 2 \Leftrightarrow c = - 2b\)
TCN: \(y = 1 \Rightarrow \dfrac{a}{b} = 1 \Leftrightarrow a = b\)
Ta có: \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\) \( \Rightarrow f'\left( x \right) = \dfrac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}}\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\)
\(\begin{array}{l} \Leftrightarrow y' > 0\,\,\,\,\,\forall x \ne 2\\ \Leftrightarrow \dfrac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}} > 0\,\,\,\forall x \ne 2\\ \Leftrightarrow ac - b > 0\\ \Leftrightarrow b.\left( { - 2b} \right) - b > 0\\ \Leftrightarrow - 2{b^2} - b > 0\\ \Leftrightarrow 2{b^2} + b < 0\\ \Leftrightarrow - \dfrac{1}{2} < b < 0\\ \Rightarrow b < 0\\ \Rightarrow a < 0,c > 0\end{array}\)
Vậy trong ba số \(a,\,\,b,\,\,c\) có 1 số dương.
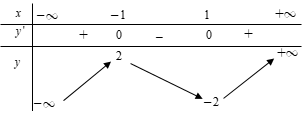
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên sau:
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số \(y = f\left( x \right)\)?
-
A.
-
B.
-
C.
-
D.
Đáp án : A
Quan sát bảng biến thiên, nhận xét các yếu tố liên quan rồi đối chiếu các đồ thị ở mỗi đáp án.
Dựa vào bảng biến thiên, ta thấy:
- Khi \(x \to + \infty \) thì \(y \to + \infty \). Loại C và D.
- Tọa độ các điểm cực trị là \(\left( { - 1;2} \right)\) và \(\left( {1; - 2} \right)\) nên đáp án A là phù hợp.
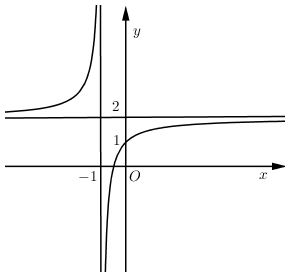
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
Chọn khẳng định đúng:
-
A.
$b + c + d = 1$
-
B.
$b + c + d = 3$
-
C.
$b + c + d = 5$
-
D.
$b + c + d = 10$
Đáp án : B
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số $ \Rightarrow c,d$.
- Tìm điểm đi qua của đồ thị hàm số $ \Rightarrow b$.
- Thay các giá trị tìm được vào kiểm tra các đáp án.
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có $\left\{ \begin{align}& \xrightarrow{TCN}y=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCD}x=-\dfrac{d}{c}=-\dfrac{d}{1}=-1\Rightarrow d=1 \\ \end{align} \right.$
Hàm số có dạng $y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)$
Ta có điểm $\left( {0;1} \right) \in \left( C \right)$
Thay $x = 0$ và $y = 1$ vào hàm số ta được $1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1$ $ \Rightarrow b + c + d = 3$
Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$
-
A.
$m = \dfrac{1}{4}$
-
B.
$m > - \dfrac{1}{2}$
-
C.
$m > - \dfrac{1}{4}$
-
D.
$m \geqslant - \dfrac{1}{4}$
Đáp án : A
- Đặt ẩn phụ $t = {x^2}$ đưa phương trình thành phương trình bậc hai ẩn $t$
- Phương trình đã cho có $4$ nghiệm phân biệt thì phương trình bậc hai ẩn $t$ có hai nghiệm dương phân biệt.
- Sử dụng định lý Vi-et để tìm $m$
Đặt ${x^2} = t\left( {t \geqslant 0} \right)$
Phương trình ${x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2} = 0$ có 4 nghiệm phân biệt thỏa mãn $x_1^2 + x_2^2 + x_3^2 + x_4^2 = 6$$ \Leftrightarrow {t^2} - 2\left( {2m + 1} \right)t + 4{m^2} = 0$ có hai nghiệm phân biệt dương thỏa mãn $2{t_1} + 2{t_2} = 6$ hay ${t_1} + {t_2} = 3$
\( \Leftrightarrow \left\{ \begin{gathered}S > 0 \hfill \\P > 0 \hfill \\\Delta ' > 0 \hfill \\ \end{gathered} \right.\) $\Leftrightarrow \left\{ \begin{gathered} 2(2m + 1) > 0 \hfill \\ 4{m^2} > 0 \hfill \\ {\left( {2m + 1} \right)^2} - 4{m^2} > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow 2\left( {2m + 1} \right) = 3$$ \Leftrightarrow m = \dfrac{1}{4}$
Cho hàm số \(y = \dfrac{{2x - 2}}{{x - 2}}\) có đồ thị là\(\left( C \right)\), \(M\)là điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)cắt hai đường tiệm cận của \(\left( C \right)\) tại hai điểm \(A\), \(B\) thỏa mãn \(AB = 2\sqrt 5 \). Gọi \(S\) là tổng các hoành độ của tất cả các điểm \(M\)thỏa mãn bài toán. Tìm giá trị của \(S\).
-
A.
\(6\)
-
B.
\(5\)
-
C.
\(8\)
-
D.
\(7\)
Đáp án : C
- Tìm 2 đường tiệm cận của đồ thị hàm số.
- Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số. Viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\).
- Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).
- Tìm giao điểm \(A,\,\,B\) của tiếp tuyến với 2 đường tiệm cận.
- Tính độ dài đoạn thẳng \(AB:\) \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).
- Giải phương trình tìm \(m\), từ đó tính \(S\).
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\). Đồ thị hàm số có hai đường tiệm cận là \(x = 2\) và \(y = 2\).
Ta có \(y' = \dfrac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}}\). Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số.
Phương trình tiếp tuyến \(d\) của \(\left( C \right)\) tại \(M\): \(y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\).
Cho \(x = 2 \Rightarrow y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {2 - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\)\( \Leftrightarrow y = \dfrac{2}{{m - 2}} + \dfrac{{2m - 2}}{{m - 2}} = \dfrac{{2m}}{{m - 2}}\).
\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(x = 2\) là \(A\left( {2;\,\dfrac{{2m}}{{m - 2}}} \right)\).
Cho \(y = 2 \Rightarrow \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}} = 2\).
\(\begin{array}{l} \Leftrightarrow - 2\left( {x - m} \right) + \left( {2m - 2} \right)\left( {m - 2} \right) = 2{\left( {m - 2} \right)^2}\\ \Leftrightarrow - 2x + 2m + 2{m^2} - 6m + 4 = 2{m^2} - 8m + 8\\ \Leftrightarrow 2x = 4m - 4 \Leftrightarrow x = 2m - 2\end{array}\)
\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(y = 2\) là \(B\left( {2m - 2;\,2} \right)\).
Ta có: \(AB = 2\sqrt 5 \Leftrightarrow {\left( {2m - 4} \right)^2} + {\left( {2 - \dfrac{{2m}}{{m - 2}}} \right)^2} = 20\)
\(\begin{array}{l} \Leftrightarrow 4{\left( {m - 2} \right)^2} + \dfrac{{16}}{{{{\left( {m - 2} \right)}^2}}} = 20\\ \Leftrightarrow {\left( {m - 2} \right)^4} - 5{\left( {m - 2} \right)^2} + 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {m - 2} \right)^2} = 1\\{\left( {m - 2} \right)^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\\m = 4\\m = 0\end{array} \right.\end{array}\)
Vậy \(S = 3 + 1 + 4 + 0 = 8\).
Cho các số dương $a, b, c, d$. Biểu thức $S = \ln \dfrac{a}{b}+ \ln \dfrac{b}{c} + \ln \dfrac{c}{d}+\ln \dfrac{d}{a}$ bằng:
-
A.
$0$
-
B.
$1$
-
C.
$\ln (\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{d}+\dfrac{d}{a})$
-
D.
$\ln (abcd)$
Đáp án : A
Sử dụng công thức: $\ln a + \ln b = \ln (a.b)$
$S = \ln \dfrac{a}{b} + \ln \dfrac{b}{c} + \ln \dfrac{c}{d} + \ln \dfrac{d}{a} = \ln \left( {\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}.\dfrac{d}{a}} \right) = \ln 1 = 0$
Cho giới hạn \(I = \mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{3x}} - {e^{2x}}}}{x}\), chọn mệnh đề đúng:
-
A.
\({I^2} + 3I = 2\)
-
B.
\({I^3} + {I^2} - 2 = 0\)
-
C.
\(\dfrac{{I - 1}}{{I + 1}} = 1\)
-
D.
\(3I - 2 = 2{I^2}\)
Đáp án : B
- Tính giới hạn \(I\) dựa vào công thức tính giới hạn \(\mathop {\lim }\limits_{x \to 0} \dfrac{{{e^x} - 1}}{x} = 1\)
- Thay giá trị \(I\) vừa tìm được vào các đáp án.
Ta có: \(I = \mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{3x}} - {e^{2x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {{e^{3x}} - 1} \right) - \left( {{e^{2x}} - 1} \right)}}{x} \)
$= \mathop {\lim }\limits_{x \to 0} \left[ {3.\dfrac{{{e^{3x}} - 1}}{{3x}} - 2.\dfrac{{{e^{2x}} - 1}}{{2x}}} \right] = 3.1 - 2.1 = 1$
Do đó, thay \(I = 1\) vào các đáp án ta được đáp án B.
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?
-
A.
\(12.\)
-
B.
\(10.\)
-
C.
\(4.\)
-
D.
\(8.\)
Đáp án : D
- Nối các đường chéo của các mặt của hình lập phương.
- Đếm số tam giác đều.
Nối các đường chéo của các mặt ta được 2 tứ diện đều không có đỉnh nào chung.
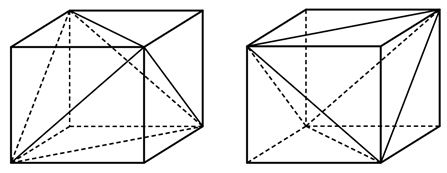
Mỗi tứ diện đều có 4 tmặt là 4 tam giác đều. Nên tổng cộng có 8 tam giác đều.
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
-
A.
\(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
-
B.
\(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
-
C.
\(\dfrac{{{a^3}\sqrt 3 }}{6}\)
-
D.
\(\dfrac{{{a^3}\sqrt 3 }}{8}\)
Đáp án : B
- Chứng minh thể tích hai khối tứ diện $MABC$ và $M{A_1}BC$ có thể tích bằng nhau.
- Tính thể tích khối tứ diện $MABC$ và suy ra đáp án.
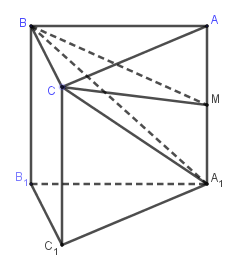
$\Delta ABC$ là tam giác đều cạnh $a$ nên có diện tích ${S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}$
Ta có $AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}$
Hai tứ diện $MABC$ và $M{A_1}BC$ có chung đỉnh $C$, diện tích hai đáy $MAB$ và $M{A_1}B$ bằng nhau nên có thể tích bằng nhau, suy ra
${V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{24}}$
Bà Hoa gửi $100$ triệu vào tài khoản định kì tính lãi suất là $8\% $ một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
-
A.
$81,412$ triệu
-
B.
$115,892$ triệu
-
C.
$119$ triệu
-
D.
$78$ triệu
Đáp án : A
- Tính số tiền bà Hoa rút ra sau 5 năm theo công thức $T = A{\left( {1 + r} \right)^N}$.
- Tính số tiền lãi lần đầu.
- Tính số tiền bà đem gửi lần 2.
- Tính số tiền sau 5 năm lần 2 theo công thức: $T = A{\left( {1 + r} \right)^N}$
- Tính số tiền lãi lần 2 và suy ra đáp số.
Số tiền bà Hoa rút sau 5 năm đầu là: $100{\left( {1 + 8\% } \right)^5} = 146,932$ triệu.
Số tiền lãi lần 1 là: $146,932 - 100 = 46,932$ triệu.
Số tiền bà gửi tiếp vào ngân hàng là: $146,932:2 = 73,466$ triệu
Số tiền và có sau 5 năm là: $73,466{\left( {1 + 8\% } \right)^5} = 107,946$ triệu.
Số tiền lãi lần 2 là: $107,946 - 73,466 = 34,480$ triệu.
Tổng số tiền lãi sau 2 lần là: $46,932 + 34,480 = 81,412$ triệu.
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
-
A.
\(\dfrac{{{a^3}\sqrt 3 }}{3}\)
-
B.
\(4{a^3}\sqrt 3 \)
-
C.
\({a^3}\sqrt 3 \)
-
D.
\(\dfrac{{4{a^3}\sqrt 3 }}{3}\)
Đáp án : D
- Xác định khoảng cách giữa hai đường thẳng \(CD\) và \(SA\) chéo nhau bằng cách tìm một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia và tính khoảng cách giữa đường thẳng và mặt phẳng song song (chính là khoảng cách từ một điểm thuộc đường thẳng đến mặt phẳng).
- Tính diện tích đáy \({S_{ABCD}}\) và chiều cao \(SO\), từ đó tính được thể tích khối chóp.
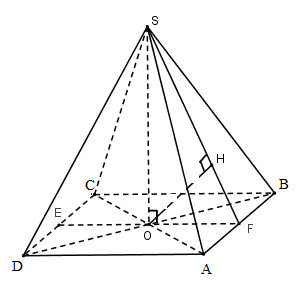
Gọi \(O = AC \cap BD\). Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Gọi $E$ và $F$ lần lượt là trung điểm của $CD$ và $AB$
Ta có:
\(\begin{array}{l}AB//CD \Rightarrow SA \subset \left( {SAB} \right)//CD\\ \Rightarrow d\left( {CD;SA} \right) = d\left( {CD;\left( {SAB} \right)} \right) = d\left( {E;\left( {SAB} \right)} \right) = 2d\left( {O;\left( {SAB} \right)} \right) = a\sqrt 3 \\ \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = \dfrac{{a\sqrt 3 }}{2}\end{array}\)
Ta có:
\(\left. \begin{array}{l}OF \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOF} \right)\)
Trong $\left( {SOF} \right)$ kẻ \(OH \bot SF\,\,\left( 1 \right)\)
Vì \(AB \bot \left( {SOF} \right) \Rightarrow AB \bot OH\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(OH \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH = \dfrac{{a\sqrt 3 }}{2}\)
Xét tam giác vuông SOF có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{F^2}}}\)
\( \Rightarrow \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{O{F^2}}} = \dfrac{4}{{3{a^2}}} - \dfrac{1}{{{a^2}}} = \dfrac{1}{{3{a^2}}} \Rightarrow SO = a\sqrt 3 \)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}a\sqrt 3 .4{a^2} = \dfrac{{4{a^3}\sqrt 3 }}{3}\)
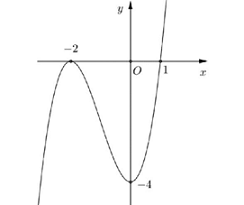
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có \(6\) nghiệm phân biệt
-
A.
\(2\).
-
B.
\(4\).
-
C.
\(3\).
-
D.
\(5\).
Đáp án : C
Đặt ẩn phụ \(t = \left| {f\left( x \right)} \right|\) để đưa về phương trình bậc hai.
Áp dụng định lý Viét để tìm nghiệm của phương trình.
Cô lập tham số m theo t rồi biện luận.
Ta có \({f^2}\left( x \right) - \left( {m + 4} \right)\left| {f\left( x \right)} \right| + 2m + 4 = 0 \)
\(\Leftrightarrow {\left| {f\left( x \right)} \right|^2} - \left( {m + 4} \right)\left| {f\left( x \right)} \right| + 2m + 4 = 0\)
$ \Leftrightarrow \left[ \begin{array}{l}
\left| {f\left( x \right)} \right| = 2\\
\left| {f\left( x \right)} \right| = m + 2
\end{array} \right.$
Dựng đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) ta được:
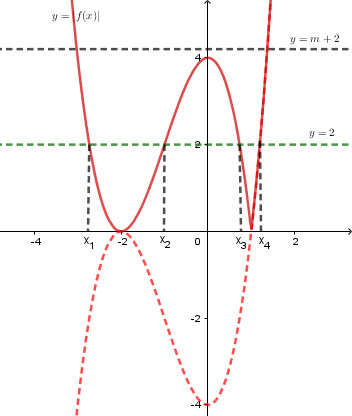
Dễ thấy phương trình \(\left| {f\left( x \right)} \right| = 2\) có \(4\) nghiệm phân biệt \({x_1},{x_2},{x_3},{x_4}\) nên để phương trình đã cho có \(6\) nghiệm phân biệt thì phương trình \(\left| {f\left( x \right)} \right| = m + 2\) phải có \(2\) nghiệm phân biệt khác các nghiệm trên.
Do đó đường thẳng \(y = m + 2\) cắt đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) tại \(2\) điểm phân biệt.
Từ hình vẽ ta có \(\left[ \begin{array}{l}m + 2 > 4\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 2\\m = - 2\end{array} \right.\).
Mà \(m \in \mathbb{Z}\) và \(m \in \left( { - 5;5} \right)\) nên \(m \in \left\{ { - 2;3;4} \right\}\).
Vậy có \(3\) giá trị thỏa mãn.
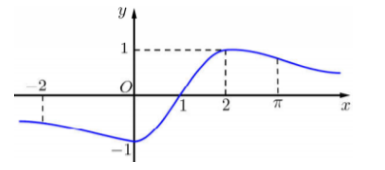
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
-
A.
\(m < f\left( 0 \right)\)
-
B.
\(m < f\left( 1 \right) - 1\)
-
C.
\(m < f\left( { - 1} \right) + 1\)
-
D.
\(m < f\left( 2 \right)\)
Đáp án : B
- Biến đổi bất phương trình về dạng \(g(x)>m\).
- Xét hàm \(y=g(x)\) và tìm GTNN của \(g(x)\).
- Bài toán thỏa khi \(m<\mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\)
\(\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}\).
Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT đồ thị hàm số \(y = f\left( x \right)\) như sau:
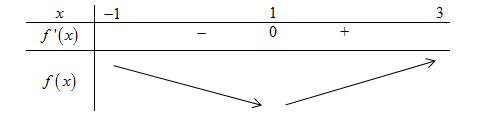
Dựa vào BBT ta thấy \(f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]\).
\(\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow - 1 \le - \sin \dfrac{{\pi x}}{2} \le 1\end{array}\)
\( \Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1\).
Vậy \(m < f\left( 1 \right) - 1\).
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A.\) Cạnh \(BC = 2a\) và \(\angle ABC = {60^0}.\) Biết tứ giác \(BCC'B'\) là hình thoi có \(\angle B'BC\) nhọn. Mặt phẳng \(\left( {BCC'B'} \right)\) vuông góc với \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ABB'A'} \right)\) tạo với \(\left( {ABC} \right)\) góc \({45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
-
A.
\(\dfrac{{\sqrt 7 {a^3}}}{7}\)
-
B.
\(\dfrac{{3\sqrt 7 {a^3}}}{7}\)
-
C.
\(\dfrac{{6\sqrt 7 {a^3}}}{7}\)
-
D.
\(\dfrac{{\sqrt 7 {a^3}}}{{21}}\)
Đáp án : B
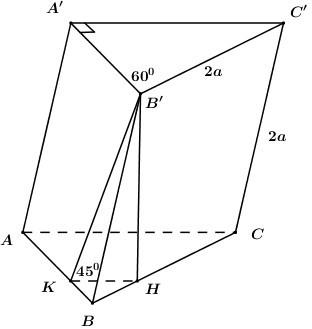
Trong \(\left( {BCC'B'} \right)\) kẻ \(B'H \bot BC\,\,\left( {H \in BC} \right)\) (do \(\angle B'BC\) nhọn).
Trong \(\left( {ABC} \right)\) kẻ \(HK\parallel AC \Rightarrow HK \bot AB\) ta có: \(\left\{ \begin{array}{l}AB \bot HK\\AB \bot B'H\end{array} \right. \Rightarrow AB \bot \left( {B'HK} \right) \Rightarrow AB \bot B'K\).
Ta có: \(\left\{ \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABC} \right) = AB\\B'K \subset \left( {ABB'A'} \right),\,\,B'K \bot AB\\HK \subset \left( {ABC} \right),\,\,HK \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {B'K;HK} \right) = \angle B'HK = {45^0}\).
\( \Rightarrow \Delta B'HK\) vuông cân tại \(H \Rightarrow B'H = HK = x\).
Xét tam giác vuông \(BB'H\) có: \(BH = \sqrt {BB{'^2} - BH{'^2}} = \sqrt {4{a^2} - {x^2}} \).
Xét tam giác vuông \(ABC\) có: \(AC = BC.\sin {60^0} = a\sqrt 3 \), \(AB = BC.\cos {60^0} = a\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{BH}}{{BC}} = \dfrac{{HK}}{{AC}} \Rightarrow \dfrac{{\sqrt {4{a^2} - {x^2}} }}{{2a}} = \dfrac{x}{{a\sqrt 3 }}\)
\(\begin{array}{l} \Leftrightarrow 3\left( {4{a^2} - {x^2}} \right) = 4{x^2}\\ \Leftrightarrow 12{a^2} - 3{x^2} = 4{x^2}\\ \Leftrightarrow {x^2} = \dfrac{{12{a^2}}}{7}\\ \Leftrightarrow x = \dfrac{{2a\sqrt {21} }}{7} = B'H\end{array}\)
\({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a.a\sqrt 3 = \dfrac{{{a^2}\sqrt 3 }}{2}\).
Vậy \({V_{ABC.A'B'C'}} = B'H.{S_{\Delta ABC}} = \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}\sqrt 7 }}{7}\).
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
