Đề kiểm tra 15 phút - Chương 1 - Đề số 3 - Đại số 10

Đề bài

Chọn phương án đúng

Câu 1. Cho mệnh đề \(\forall x \in R,{x^2} > 0\). Phủ định mệnh đề trên là

A.\(\forall x \in \mathbb{R},{x^2} < 0\)

B.\(\forall x \in \mathbb{R},{x^2} \le 0\)

C.\(\exists x \in \mathbb{R},{x^2} \le 0\)

D.\(\exists x \in \mathbb{R},{x^2} < 0\)

Câu 2. Cho mệnh đề chứa biến \(P(x):x + 15 \le {x^2}\) với \(x \in \mathbb{R}.\) Mệnh đề nào sau đây là mệnh đề đúng

A.P(0)                    B.P(5)

C.P(2)                     D.P(4)

Câu 3. Trong các mệnh đề sau, mệnh đề nào không phải là định lý

A.\(\forall n \in \mathbb{N},{n^2} \;\vdots\; 2 \Rightarrow n \;\vdots \;2\)

B.\(\forall n \in \mathbb{N},{n^2} \;\vdots \;3 \Rightarrow n \;\vdots \;3\)

C.\(\forall n \in \mathbb{N},{n^2}\; \vdots \;9 \Rightarrow n \;\vdots \;9\)

D.\(\forall n \in \mathbb{N},{n^2}\; \vdots\; 6 \Rightarrow n \;\vdots\; 6\)

Câu 4. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng

A.\(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)

B.\(\forall x \in \mathbb{R},x >  - 1 \Rightarrow {x^2} > 1\)

C.\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\)

D.\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x >  - 1\)

Câu 5. Cho tập A có 5 phần tử. Số tập con có 2 phần tử của A là

A.8                           B.10

C.12                         D.14

Câu 6. Cho hai tập \(A = \left\{ {x \in \mathbb{R}|x + 3 < 5 + 2x} \right\},\)\(\;{\rm{ B = }}\left\{ {x \in \mathbb{R}|5x - 4 < 4x - 1} \right\}\)

Tất cả các số tự nhiên thuộc tập \(A \cap B\) là

A. \(0,1,2\)                     B. \(0,1\)

C. \(1,2\)                        D. \(-1,0,1,2\)

Câu 7. Cho số \(a{\rm{ }} < {\rm{ }}0\). Điều kiện cần và đủ để hai tập \(( - \infty ;5a)\) và \(\left( {\dfrac{5}{a}; + \infty } \right)\) có giao khác rỗng là

A.\( - 1 \le a < 0\)                 B.\(a \le  - 1\)

C.\(a < -1\)                        D.\(-1< a <0\)

Câu 8. Cho các tập hợp \(A = \left\{ {x \in \mathbb{R}|f(x) = 0} \right\},\)\(\;B = \left\{ {x \in \mathbb{R}|g(x) = 0} \right\}\) và \(C = \left\{ {x \in \mathbb{R}|{f^2}(x) + {g^2}(x) = 0} \right\}\). Khi đó

A. \(C = A \cup B\)                B. \(C = A\backslash B\)

C. \(C=B\backslash A\)                   D. \(A \cap B\)

Câu 9. Cho các tập \(A = \left[ { - 5;4} \right],\)\(\,{\rm{ B = }}\left( { - 3;2} \right)\). Khi đó

A.\(A\backslash B = \left[ { - 5; - 4} \right] \cup \left[ {3;4} \right]\)

B.\(A\backslash B = \left[ { - 5; - 3} \right] \cup \left[ {2;4} \right]\)

C.\(A\backslash B = \left[ { - 5; - 3} \right]\)

D.\(A\backslash B = \left[ { - 5;\left. { - 3} \right) \cup \left( {2;\left. 4 \right]} \right.} \right.\)

Câu 10. Mệnh đề nào sau đây là mệnh đề đúng

A.\(E \subset E \cap F\)

B.\(E \cup F \subset F\)

C.\(E = (E\backslash F) \cup (E \cap F)\)

D.\(E \cup F = (E\backslash F) \cup (F\backslash E)\)

Lời giải chi tiết

Câu 1. Chọn C.

Áp dụng: Phủ định của mệnh đề “\(\forall x \in X,P(x)\)” là mệnh đề “\(\exists x \in X,\overline {P(x)} \) “.

Phủ định của mệnh đề \(\forall x \in R,{x^2} > 0\) là \(\exists x \in \mathbb{R},{x^2} \le 0\)

Câu 2. Chọn B.

\(P(5):5 + 15 \le 25\) là mệnh đề đúng.

Câu 3. Chọn C.

Với \(n = 3\) thì \({n^{2\;}}{\rm{ = }}9\) chia hết cho 9 nhưng \(n\) không chia hết cho 9 nên mệnh đề C sai hay nó không phải định lý.

Câu 4. Chọn A.

Hiển nhiên \(x > 1\) thì \({x^2}\; > 1\).

Câu 5. Chọn B.

Giả sử \(A = \left\{ {a;b;c;d;e} \right\}\) . Các tập con có hai phần tử của \(A\) là

\(\left\{ {a;b} \right\},\left\{ {a;c} \right\},\left\{ {a;d} \right\},\left\{ {a;e} \right\},\left\{ {b;c} \right\},\)\(\;\left\{ {b;d} \right\},\left\{ {b;e} \right\},\left\{ {c;d} \right\},\left\{ {c;e} \right\},\left\{ {d;e} \right\}\) .

Có tất cả 10 tập như vậy.

Câu 6. Chọn A.

Ta có: \(x + 3 < 5 + 2x \Leftrightarrow x >  - 2\) . Suy ra \(A = \left( { - 2; + \infty } \right)\) .

Tương tự \(5x - 4 < 4x - 1 \Leftrightarrow x < 3\) . Suy ra \(B = \left( { - \infty ;3} \right)\) .

\( \Rightarrow A \cap B = \left( { - 2;3} \right)\)

Mà các số cần tìm là số tự nhiên nên ta có các số thỏa mãn là 0;1;2.

Câu 7. Chọn D.

Hai tập đã cho có giao khác rỗng khi và chỉ khi

\(\dfrac{5}{a} < 5a  \Leftrightarrow 5 > 5{a^2}\) (nhân cả hai vế với \(a < 0\))

\( \Leftrightarrow {a^2} < 1 \Leftrightarrow  - 1 < a < 1\)

Kết hợp với \(a < 0\) ta được \(-1 < a < 0\).

Câu 8. Chọn D

\(\begin{array}{l}x \in C \Leftrightarrow {f^2}(x) + {g^2}(x) = 0\\ \Leftrightarrow \left\{ \begin{array}{l}f(x) = 0\\g(x) = 0\end{array} \right.\\{\rm{        }} \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right. \Leftrightarrow x \in A \cap B\end{array}\) .

Vậy \(C = A \cap B\) .

Câu 9. Chọn B.

Biểu diễn các tập hợp trên trục số để suy ra kết quả.

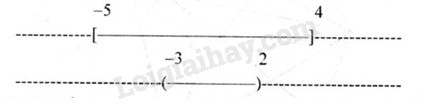
Vậy \(A\backslash B = \left[ { - 5; - 3} \right] \cup \left[ {2;4} \right]\).

Câu 10. Chọn C.

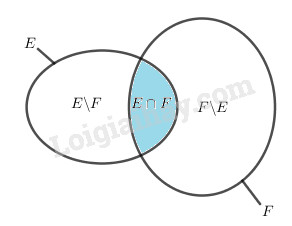
Kiểm tra hệ thức \(E = \left( {E\backslash F} \right) \cup \left( {E \cap F} \right)\) bằng biểu đồ Ven.

Đáp án A: sai vì \(E \cap F \subset E\)

Đáp án B: sai vì \(F \subset E \cup F\)

Đáp án D: sai vì \(E \cup F = \left( {E\backslash F} \right) \cup \left( {F\backslash E} \right) \cup \left( {E \cap F} \right)\)

Loigiaihay.com