Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 7
Đề bài
Bài 1. Hãy chỉ ra giả thiết và kết luận của định lí: “hai đường thẳng phân biệt cùng vuong góc với đường thứ ba thì chúng song song với nhau”.
Bài 2. Hãy chứng minh định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị nhau”.
Phương pháp giải - Xem chi tiết
Sử dụng:
Định lí thường phát biểu dưới dạng: " Nếu \(A\) thì \(B\)" với \(A\) là giả thiết, là điều kiện cho biết; \(B\) là kết luận, là điều được suy ra.
Tiên đề Ơ-clit
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
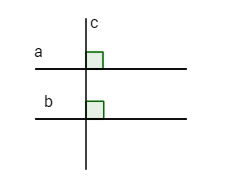
Bài 1. GT: \(\eqalign{ & a \bot c \cr & b \bot c \cr} \)
KL: a//b
Bài 2.
GT: a // b
C cắt a tại A, c cắt b tại B
KL: \(\widehat {{A_1}} = \widehat {{B_1}}\)
Chứng minh:
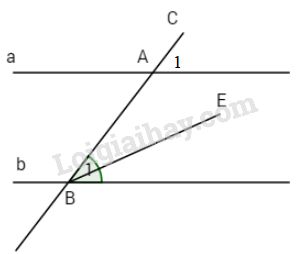
Giả giử \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\) bằng nhau.
Như vậy qua B ta có thể vẽ được tia BE sao cho \(\widehat {ABE}\) và \(\widehat {{A_1}}\) ở vị trí đồng vị \( \Rightarrow BE//a\).
Lại có b qua B và b//a. Như vậy qua một điểm B ta có BE và b cùng song song với a.
Theo tiên đề Oclit, BE và b phải trùng nhau.
Hay \(\widehat {{A_1}} = \widehat {{B_1}}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 1 - Hình học 7
- Bài 53 trang 102 SGK Toán 7 tập 1
- Bài 52 trang 101 SGK Toán 7 tập 1
- Bài 51 trang 101 SGK Toán 7 tập 1
- Bài 50 trang 101 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
